|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Рекурсия и деревья
Рекурсивные алгоритмы для бинарных деревьев
Алгоритмы обхода дерева, рассмотренные в разделе 5.6, наглядно демонстрируют необходимость изучения рекурсивных алгоритмов для бинарных деревьев, что обусловлено рекурсивной структурой этих деревьев. Для решения многих задач можно непосредственно применять рекурсивные алгоритмы вида "разделяй и властвуй ", которые, по сути, обобщают алгоритмы обхода деревьев. Обработка дерева сводится к обработке корневого узла и (рекурсивно) его поддеревьев, и вычисление можно выполнять перед, между или после рекурсивных вызовов (или же использовать все три метода).
Часто требуется определить различные структурные параметры дерева, имея только ссылку на него. Например, программа 5.17 содержит рекурсивные функции для вычисления количества узлов и высоты заданного дерева. Эти функции написаны непосредственно исходя из определения 5.6. Ни одна из этих функций не зависит от порядка обработки рекурсивных вызовов: они обрабатывают все узлы дерева и возвращают одинаковый результат для любого порядка рекурсивных вызовов. Не все параметры дерева вычисляются так легко: например, программа для эффективного вычисления длины внутреннего пути бинарного дерева более сложна (см. упражнения 5.88 - 5.90).
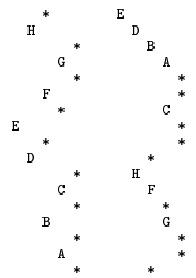
Еще одна функция, которая бывает нужна при создании программ, обрабатывающих деревья - функция, которая выводит структуру дерева или вычерчивает его. Например, программа 5.18 представляет собой рекурсивную процедуру, выводящую дерево в формате, приведенном на рис. 5.29. Эту же базовую рекурсивную схему можно использовать для вычерчивания более сложных представлений деревьев, подобных приведенным на рисунках в этой книге (см. упражнение 5.85).
Левая часть получена в результате работы программы 5.18 с деревом, приведенным на рис. 5.26. В ней приведена структура дерева, подобная графическому представлению, которое используется в данной книге, но повернутая на 90 градусов. Правая часть получена в результате выполнения этой же программы, где оператор вывода перемещен в начало программы; здесь показана структура дерева в привычном схематическом формате.
Программа 5.18 выполняет поперечный обход, а если выводить элемент перед рекурсивными вызовами, получится прямой обход; этот вариант также приведен на рис. 5.29.
Программа 5.17. Вычисление параметров дерева
Для выяснения базовых структурных свойств дерева можно использовать такие рекурсивные процедуры.
int count(link h)
{
if (h == 0) return 0;
return count(h ->l) + count(h ->r) + 1;
}
int height(link h)
{
if (h == 0) return -1;
int u = height(h ->l), v = height(h ->r);
if (u > v) return u+1; else return v+1;
}
Программа 5.18. Функция быстрого вывода дерева
Эта рекурсивная программа отслеживает высоту дерева и использует эту информацию для подсчета отступов при выводе представления, которое можно использовать для отладки программ обработки деревьев (см. рис. 5.29). Здесь предполагается, что элементы в узлах имеют тип Item, для которого определена перегруженная операция <<.
void printnode(Item x, int h)
{ for (int i = 0; i < h; i++) cout << " ";
cout << x << endl;
}
void show(link t, int h)
{
if (t == 0) { printnode('*', h); return; }
show(t ->r, h+1);
printnode(t ->item, h);
show(t ->l, h+1);
}
Такой формат применяется для вывода генеалогического дерева, списка файлов в древовидной файловой структуре или при создании структуры печатного документа. Например, прямой обход дерева, приведенного на рис. 5.19, выводит оглавление этой книги.
Первым примером программы, которая строит древовидную структуру, будет приложение определения максимума, которое было рассмотрено в разделе 5.2. Наша цель - построение турнира, т.е. бинарного дерева, в котором элементом каждого внутреннего узла является копия большего из элементов его двух дочерних элементов. Тогда элемент в корне является копией наибольшего элемента в турнире. Элементы в листья (узлах без дочерних узлов) содержат исследуемые данные, а остальная часть дерева - структура данных, которая позволяет эффективно находить наибольший из элементов.
Программа 5.19 - рекурсивная программа, которая строит турнир из элементов массива. Будучи расширенной версией программы 5.6, она использует стратегию "разделяй и властвуй ": чтобы построить турнир для единственного элемента, программа создает лист, содержащий этот элемент, и возвращает этот элемент. Чтобы построить турнир для N > 1 элементов, программа делит все множество элементов пополам, строит турнир для каждой половины и создает новый узел со ссылками на эти два турнира и с элементом, который является копией большего элемента в корнях обоих турниров.
На рис. 5.30 приведен пример древовидной структуры, построенной программой 5.19. Иногда построение таких рекурсивных структур бывает предпочтительнее отыскания максимума простым перебором данных, как это было сделано в программе 5.6, поскольку древовидная структура обеспечивает возможность выполнения других операций. Важным примером служит и сама операция, использованная для построения турнира. При наличии двух турниров их можно объединить в один турнир, создав новый узел, левая ссылка которого указывает на один турнир, а правая на другой, и приняв больший из двух элементов (в корнях двух данных турниров) в качестве наибольшего элемента объединенного турнира. Можно также рассмотреть алгоритмы добавления и удаления элементов и выполнения других операций. Здесь мы не станем рассматривать такие операции, поскольку аналогичные структуры данных с подобными функциями будут рассмотрены в "Очереди с приоритетами и пирамидальная сортировка" .
Вообще -то реализации с использованием деревьев для нескольких из АТД обобщенных очередей (рассмотренных в разделе 4.6 "Абстрактные типы данных" ) являются основной темой обсуждения в значительной части этой книги. В частности, многие из алгоритмов, приведенных в главах 12 - 15, основываются на деревьях бинарного поиска (binary search tree) - это деревья, соответствующие бинарному поиску, аналогично тому, как структура на рис. 5.30 соответствует рекурсивному алгоритму отыскания максимума (см. рис. 5.6). Сложность реализации и использования таких структур заключается в обеспечении их эффективности после выполнения большого числа операций вставить, удалить и т.п.
Вторым примером программы создания бинарного дерева служит измененная версия программы вычисления префиксного выражения из раздела 5.1 (программа 5.4), которая не просто вычисляет префиксное выражение, а создает представляющее его дерево (см. р рис. 5.31). В программе 5.20 используется та же рекурсивная схема, что и в программе 5.4, но рекурсивная функция возвращает не значение, а ссылку на дерево.
Программа создает новый узел дерева для каждого символа в выражении: узлы, которые соответствуют операциям, содержат ссылки на свои операнды, а листовые узлы содержат переменные (или константы), которые являются входными данными выражения.
Программа 5.19. Построение турнира
Данная рекурсивная функция делит массив a[1], ..., a[r] на две части a[1], ..., a[m] и a[m+1], ..., a[r], строит (рекурсивно) турниры для этих двух частей и создает турнир для всего массива, установив ссылки в новом узле на рекурсивно построенные турниры и поместив в него копию большего элемента из корней двух рекурсивно построенных турниров.
struct node
{ Item item; node *l, *r;
node(Item x)
{ item = x; l = 0; r = 0; }
};
typedef node* link;
link max(Item a[], int l, int r)
{ int m = (l+r)/2;
link x = new node(a[m]);
if (l == r) return x;
x ->l = max(a, l, m);
x ->r = max(a, m+1, r);
Item u = x ->l ->item, v = x ->r ->item;
if (u > v) x ->item = u; else x ->item = v;
return x;
}
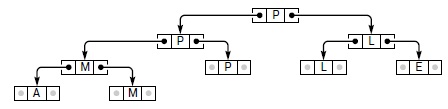
На этом рисунке показана структура дерева, созданная программой 5.19 из входных данных A M P L E. Элементы данных находятся в листьях. Каждый внутренний узел содержит копию большего из элементов в двух дочерних узлах, так что по индукции наибольший элемент находится в корне.
В программах трансляции наподобие компиляторов часто используются такие внутренние представления программ, поскольку деревья удобны по многим соображениям. Например, можно представить операнды, которые соответствуют принимающим значения переменным, и сгенерировать машинный код для вычисления выражения, представленного в виде дерева с обратным обходом. А можно использовать дерево с поперечным обходом для вывода выражения в инфиксной форме или дерево с обратным обходом - для вывода выражения в постфиксной форме.
В этом разделе было рассмотрено несколько примеров, демонстрирующих тезис о возможности создания и обработки связных древовидных структур с помощью рекурсивных программ. Чтобы этот подход стал эффективным, потребуется учесть производительность различных алгоритмов, альтернативные представления, нерекурсивные варианты и ряд других нюансов. Однако мы отложим более подробное изучение программ обработки деревьев до "Таблицы символов и деревья бинарного поиска" , поскольку в лекциях 7 - 11 деревья используются в основном в описательных целях. К явным реализациям деревьев мы вернемся в "Таблицы символов и деревья бинарного поиска" , поскольку они служат основой для многих алгоритмов, рассматриваемых в лекциях 12 - 15 .
Программа 5.20. Создание дерева синтаксического анализа
Используя ту же стратегию, которая была задействована для вычисления префиксных выражений (см. программу 5.4), эта программа создает из префиксного выражения дерево синтаксического анализа. Для простоты предполагается, что операндами являются одиночные символы. Каждый вызов рекурсивной функции создает новый узел, передавая в него в качестве лексемы следующий символ из входных данных. Если лексема представляет собой операнд, программа возвращает новый узел, а если операцию, то устанавливает левый и правый указатели на деревья, построенные (рекурсивно) для двух аргументов.
char *a; int i;
struct node
{ Item item; node *l, *r;
node(Item x)
{ item = x; l = 0; r = 0; }
};
typedef node* link;
link parse()
{ char t = a[i++];
link x = new node(t);
if ((t == '+') || (t == '*'))
{ x ->l = parse(); x ->r = parse(); }
return x;
}
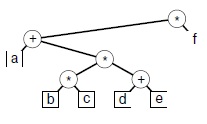
Это дерево создано программой 5.20 для префиксного выражения * + a * * b c + d e f. Оно представляет собой естественный способ представления выражения: каждый операнд размещается в листе (который показан здесь в качестве внешнего узла), а каждая операция должна выполняться с выражениями, которые представлены левым и правым поддеревьями узла, содержащего операцию.
Упражнения
5.85. Измените программу 5.18, чтобы она выводила PostScript -программу, которая вычерчивает дерево в формате как на рис. 5.23, но без квадратиков, представляющих внешние узлы. Для вычерчивания линий используйте функции moveto и lineto, а для отрисовки узлов - пользовательскую операцию
/node {newpath moveto currentpoint 4 0 360 arc fill} def
После инициализации этого определения вызов node приводит к помещению черной точки с координатами, которые находятся в стеке (см. "Абстрактные типы данных" ).
5.86. Напишите программу, которая подсчитывает листья в бинарном дереве.
5.87. Напишите программу, которая подсчитывает количество узлов в бинарном дереве с одним внешним и одним внутренним дочерними узлами.
5.88. Напишите рекурсивную программу, которая вычисляет длину внутреннего пути бинарного дерева, используя определение 5.6.
5.89. Определите количество вызовов функций, выполненных программой при вычислении длины внутреннего пути бинарного дерева. Докажите ответ методом индукции.
5.90. Напишите рекурсивную программу, которая вычисляет длину внутреннего пути бинарного дерева за время, пропорциональное количеству узлов в дереве.
5.91. Напишите рекурсивную программу, которая удаляет из турнира все листья с заданным ключом (см. упражнение 5.59).