|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Рекурсия и деревья
Упражнения
5.37. Напишите функцию, которая вычисляет FN mod M, используя для промежуточных вычислений постоянный объем памяти.
5.38. Каково наибольшее значение N, для которого FN может быть представлено в виде 64 -разрядного целого числа?
5.39. Нарисуйте дерево, которое соответствует рис. 5.15 для случая, когда рекурсивные вызовы в программе 5.11 поменяны местами.
5.40. Напишите функцию, которая использует восходящее динамическое программирование для вычисления значения PN, определяемого рекуррентным соотношением
Pn = LN/ 2j + P Ln/ 2j + P n2i, для N > 1, при P0 = 0.
Нарисуйте график зависимости PN - N IgN/ 2 от N для 0 < N < 1024.
5.41. Напишите функцию, в которой восходящее динамическое программирование используется для решения упражнения 5.40.
5.42. Нарисуйте дерево, которое соответствует рис. 5.15 для функции из упражнения 5.41 при вызове с аргументом N = 23.
5.43. Нарисуйте график зависимости от N количества рекурсивных вызовов, выполняемых функцией из упражнения 5.41 для вычисления PN при 0 < N < 1024. (При этом для каждого значения N программа должна запускаться заново.)
5.44. Напишите функцию, в которой восходящее динамическое программирование используется для вычисления значения CN, определяемого рекуррентным соотношением
CN = N + N ? (кj + CN_k), для N > 1, при C0 = 1.
N 1< к < N
5.45. Напишите функцию, в которой нисходящее динамическое программирование применяется для решения упражнения 5.44.
5.46. Нарисуйте дерево, которое соответствует рис. 5.15 для функции из упражнения 5.45 при вызове с аргументом N = 23.
5.47. Нарисуйте график зависимости от N количества рекурсивных вызовов, выполняемых функцией из упражнения 5.45 для вычисления CN при 0 < N < 1024. (При этом для каждого значения N программа должна запускаться заново.)
5.48. Приведите содержимое массивов maxKnown и itemKnown, вычисленное программой 5.13 для вызова knap(17) с элементами, приведенными на рис. 5.16.
5.49. Приведите дерево, соответствующее рис. 5.18, если элементы рассматриваются в порядке уменьшения их размеров.
5.50. Докажите лемму 5.3.
5.51. Напишите функцию, решающую задачу о ранце, с помощью варианта программы 5.12, в котором применяется восходящее динамическое программирование.
5.52. Напишите функцию, которая решает задачу о ранце методом нисходящего динамического программирования, но используя при этом рекурсивное решение, основанное на вычислении оптимального количества конкретного элемента, который должен быть помещен в ранец, когда (рекурсивно) известен оптимальный способ упаковки ранца без этого элемента.
5.53. Напишите функцию, которая решает задачу о ранце с помощью варианта рекурсивного решения, описанного в упражнении 5.52, в котором применяется восходящее динамическое программирование.
5.54. Воспользуйтесь динамическим программированием для решения упражнения 5.4. Наблюдайте за общим количеством сохраняемых вызовов функций.
5.55. Напишите программу для вычисления биномиального коэффициента I I с помощью нисходящего динамического программирования, исходя из рекуррентного соотношения
Деревья
Деревья - это математическая абстракция, играющая главную роль при разработке и анализе алгоритмов, поскольку
- деревья используются для описания динамических свойств алгоритмов;
- часто создаются и используются структуры данных, которые являются конкретными реализациями деревьев.
Мы уже встречались с примерами обоих применений деревьев. В "Введение" были разработаны алгоритмы для решения задачи связности, которые основаны на древовидных структурах, а в разделах 5.2 и 5.3 структура вызовов рекурсивных алгоритмов была описана с помощью древовидных структур.
Мы часто встречаемся с деревьями в повседневной жизни - это основное понятие очень хорошо знакомо. Например, многие люди графически обозначают связь предков и наследников в виде генеалогического дерева; как мы увидим, значительная часть терминов заимствована именно из этой области. Еще один пример - организация спортивных турниров; в частности, исследованием этого применения занимался Льюис Кэрролл. В качестве третьего примера можно привести организационную диаграмму большой корпорации; это применение напоминает иерархическое разделение, характерное для алгоритмов "разделяй и властвуй ". Четвертым примером служит дерево синтаксического разбора предложения английского (или любого другого языка) на составляющие его части; такие деревья тесно связаны с обработкой компьютерных языков, как описано в части V. Типичный пример дерева - в данном случае описывающего структуру глав этой книги - показан на рис. 5.19. Далее в книге нам встретится и множество других примеров применения деревьев.
Одно из наиболее известных применений древовидных структур в компьютерных приложениях - организация файловых систем. Файлы хранятся в каталогах (иногда называемых также папками), которые рекурсивно определяются как последовательности каталогов и файлов. Это рекурсивное определение снова отражает естественное рекурсивное разбиение на составляющие и идентично определению определенного типа дерева.
Существует множество различных типов деревьев, и важно понимать различие между абстракцией и конкретным представлением, с которым выполняется работа для данного приложения. Поэтому мы подробно рассмотрим различные типы деревьев и их представления. Рассмотрение начнется с определения деревьев как абстрактных объектов и с введения большей части основных связанных с ними терминов. Мы неформально рассмотрим различные необходимые нам типы деревьев в порядке сужения этого понятия:
- Деревья
- Деревья с корнем
- Упорядоченные деревья
- M -арные и бинарные деревья
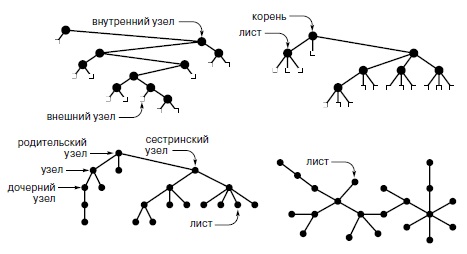
После этого неформального рассмотрения мы перейдем к формальным определениям и рассмотрим различные представления и применения. На рис. 5.20 показаны многие из этих базовых концепций, которые будут сначала рассмотрены, а затем и определены.
Дерево (tree) - это непустая коллекция вершин и ребер, удовлетворяющих определенным требованиям. Вершина (vertex) - это простой объект (называемый также узлом (node)), который может иметь имя и содержать другую связанную с ним информацию; ребро (edge) - это связь между двумя вершинами. Путь (path) в дереве - это список отдельных вершин, в котором последовательные вершины соединены ребрами дерева. Определяющее свойство дерева - существование только одного пути, соединяющего любые два узла. Если между какой -либо парой узлов существует более одного пути, или если между какой -либо парой узлов путь отсутствует, то это граф, а не дерево. Несвязанное множество деревьев называется лесом (forest).
Дерево с корнем (rooted) - это дерево, в котором один узел назначен корнем (root) дерева. В компьютерных науках термин дерево обычно применяется к деревьям с корнем, а термин свободное дерево (free tree) - к более общим структурам, описанным в предыдущем абзаце. В дереве с корнем любой узел является корнем поддерева, состоящего из него и расположенных под ним узлов.
Это дерево описывает части, главы и соответствующие им разделы данной книги. Каждый элемент представлен узлом. Каждый узел связан нисходящими связями с составляющими его частями и восходящей связью - с большей частью, к которой он принадлежит.
На этих схемах приведены примеры бинарного дерева (вверху слева), тернарно го дерева (вверху справа), дерева с корнем (внизу слева) и свободного дерева (внизу справа).
Существует только один путь между корнем и каждым из других узлов дерева. Данное определение никак не определяет направление ребер; и в зависимости от конкретной ситуации можно считать, что все ребра указывают или от корня, или к корню. Обычно деревья рисуются с корнем вверху (хотя поначалу это соглашение кажется неестественным) и говорят, что узел у располагается под узлом x (а x располагается над у), если x находится на пути от у к корню (т.е., у находится под х, как нарисовано на странице, и соединяется с х путем, который не проходит через корень). Каждый узел (за исключением корня) имеет только один узел над ним, который называется его родительским узлом (parent); узлы, расположенные непосредственно под данным узлом, называются его дочерними узлами (child). Иногда аналогия с генеалогическими деревьями распространяется дальше, и тогда говорят о " бабушках " (grand parent) или " сестрах " (sibling) данного узла.
Узлы, не имеющие дочерних узлов, называются листьями (leaf) или терминальными (оконечными, terminal) узлами. И, соответственно, узлы, имеющие хотя бы один дочерний узел, иногда называются нетерминальными (nonterminal) узлами. В этой главе мы уже встречались с различным применением этих типов узлов. В деревьях, которые использовались для представления структуры вызовов рекурсивных алгоритмов (например, на рис. 5.14), нетерминальные узлы (кружки) представляют вызовы функций с рекурсивными вызовами, а терминальные узлы (квадратики) представляют вызовы функций без рекурсивных вызовов.
В некоторых приложениях способ упорядочения дочерних узлов каждого узла имеет значение; в других это не важно. Упорядоченное (ordered) дерево - это дерево с корнем, в котором определен порядок следования дочерних узлов каждого узла. Упорядоченные деревья - естественное представление: ведь при рисовании дерева дочерние узлы размещаются в определенном порядке. Действительно, многие другие конкретные представления имеют аналогично предполагаемый порядок; например, обычно это различие имеет значение при работе с компьютерными представлениями деревьев.
Если каждый узел должен иметь конкретное количество (M) дочерних узлов, расположенных в конкретном порядке, мы имеем M -арное дерево. В таком дереве часто можно определить специальные внешние узлы, которые не имеют дочерних узлов. Тогда внешние узлы можно задействовать в качестве фиктивных, чтобы на них ссылались узлы, не имеющие должного количества дочерних узлов. В частности, простейшим типом M -арного дерева является бинарное дерево. Бинарное дерево (binary tree) - это упорядоченное дерево, состоящее из узлов двух типов: внешних узлов без дочерних узлов и внутренних узлов, каждый из которых имеет ровно два дочерних узла. Поскольку два дочерних узла каждого внутреннего узла упорядочены, можно говорить о левом дочернем узле (left child) и правом дочернем узле (right child) внутренних узлов. Каждый внутренний узел должен иметь и левый, и правый дочерние узлы, хотя один из них или оба могут быть внешними узлами. Лист в M -арном дереве - это внутренний узел, все дочерние узлы которого являются внешними.
Все это общая терминология. Далее рассматриваются формальные определения, представления и приложения в порядке расширения понятий:
- бинарные и M -арные деревья
- упорядоченные деревья
- деревья с корнем
- свободные деревья
Начнем с наиболее специфической абстрактной структуры - как мы увидим, это позволит подробно рассмотреть конкретные представления.
Определение 5.1. Бинарное дерево - это либо внешний узел, либо внутренний узел, связанный с (упорядоченной - прим. перев.) парой бинарных деревьев, которые называются левым и правым поддеревьями этого узла.
Из этого определения понятно, что само бинарное дерево - абстрактное математическое понятие. При работе с компьютерным представлением мы работаем лишь с одной конкретной реализацией этой абстракции. Эта ситуация не отличается от представления действительных чисел значениями типа float, целых чисел значениями типа int и т.д. Когда мы рисуем дерево с узлом в корне, связанным ребрами с левым поддеревом, расположенным слева, и с правым поддеревом, расположенным справа, мы выбираем удобное конкретное представление. Существует множество различных способов представления бинарных деревьев (см., например, упражнение 5.62), которые поначалу несколько шокируют, но если учесть абстрактный характер определения, они вполне допустимы.
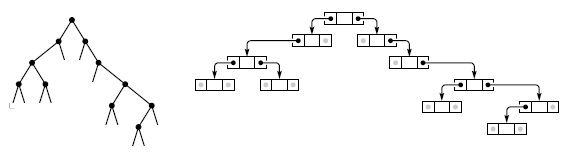
При реализации программ, использующих и обрабатывающих бинарные деревья, чаще всего применяется следующее конкретное представление - структура с двумя ссылками (левой и правой) для внутренних узлов (см. рис. 5.21). Эти структуры похожи на связные списки, но имеют по две ссылки в каждом узле, а не по одной. Пустые ссылки соответствуют внешним узлам. Так что мы просто добавили ссылку в стандартное представление связного списка, приведенное в разделе 3.3 "Элементарные структуры данных" :
struct node { Item item; node *l, *r; }
typedef node *link;
Это просто код C++ для определения 5.1. Узлы состоят из элементов и пар указателей на узлы; указатели на узлы называются также ссылками. Так, например, абстрактная операция переход к левому поддереву реализуется с помощью обращения через указатель наподобие x = x ->l.
Это стандартное представление позволяет построить эффективную реализацию операций, в которых нужны перемещения по дереву вниз от корня, но не перемещения по дереву вверх от дочернего узла к его родительскому узлу. Для алгоритмов, где требуются такие операции, можно добавить в каждый узел третью ссылку, направленную к его родительскому узлу. Эта альтернатива аналогична двухсвязным спискам. Как и в случае со связными списками (см. рис. 3.6), в некоторых ситуациях удобнее хранить узлы дерева в массиве и использовать в качестве ссылок индексы, а не указатели. Конкретный пример такой реализации будет рассмотрен в разделе 12.7 "Таблицы символов и деревья бинарного поиска" . Для определенных специальных алгоритмов используются и другие представления бинарных деревьев - мы будем обращаться к ним в основном в "Очереди с приоритетами и пирамидальная сортировка" .
В стандартном представлении бинарного дерева используются узлы с двумя ссылками: левая указывает на левое поддерево, а правая - на правое поддерево. Пустые ссылки соответствуют внешним узлам.
Из -за наличия такого множества различных возможных представлений можно было бы разработать АТД бинарного дерева, который позволяет инкапсулировать важные для нас операции и отделить использование от реализации этих операций. В данной книге такой подход не используется, поскольку
- чаще всего будет использоваться представление с двумя ссылками;
- деревья будут применяться для реализации АТД более высокого уровня, и мы хотим сосредоточить внимание на этих АТД;
- эффективность алгоритмов может зависеть от конкретного представления - это обстоятельство может быть упущено в АТД.
Это те же причины, по которым мы используем знакомые конкретные представления массивов и связных списков. Представление бинарного дерева, показанное на рис. 5.21 - один из фундаментальных инструментов, который теперь добавлен к этому краткому списку.
Изучение связных списков мы начали с рассмотрения элементарных операций вставки и удаления узлов (см. рис. 3.3 и рис. 3.4). При использовании стандартного представления бинарных деревьев такие операции совсем не обязательно будут элементарными из -за наличия второй ссылки. Если нужно удалить узел из бинарного дерева, то возникает принципиальная проблема наличия двух дочерних узлов, с которыми нужно что -то делать после удаления узла, и только одного родительского. Существуют три естественных операции, для которых подобное осложнение не возникает: вставка нового узла в нижнюю часть дерева (замена пустой ссылки ссылкой на новый узел), удаление листа (замена ссылки на него пустой ссылкой) и объединение двух деревьев посредством создания нового корня, левая ссылка которого указывает на одно дерево, а правая - на другое. Эти операции интенсивно используются при работе с бинарными деревьями.
Определение 5.2. M -арное дерево - это либо внешний узел, либо внутренний узел, связанный с упорядоченной последовательностью M деревьев, которые также являются M -арными деревьями.
Обычно узлы в M -арных деревьях представляются либо в виде структур с M именованными ссылками (как в бинарных деревьях), либо в виде массивов M ссылок. Например, в главе 15 "Поразрядный поиск" рассмотрены 3 -арные (или тернарные) деревья, в которых используются структуры с тремя именованными ссылками (левой, средней и правой), каждая из которых имеет специальное значение для связанных с этими деревьями алгоритмов. В остальных случаях вполне годится хранение ссылок в массивах, поскольку значение M фиксировано - хотя, как мы увидим, при использовании такого представления нужно внимательно следить за объемом использованной памяти.
Определение 5.3. Дерево (называемое также упорядоченным деревом) - это узел (называемый корнем), связанный с последовательностью несвязанных деревьев. Такая последовательность называется лесом.
Различие между упорядоченными деревьями и M -арными деревьями состоит в том, что узлы в упорядоченных деревьях могут иметь любое количество дочерних узлов, а узлы в M -арных деревьях должны иметь точно M дочерних узлов. Иногда, если нужно различать упорядоченные и M -арные деревья, используется термин обобщенное дерево (general tree).
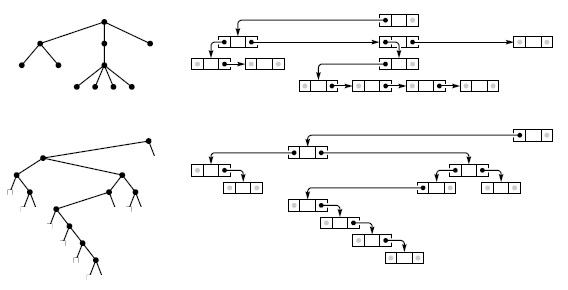
Поскольку каждый узел в упорядоченном дереве может иметь любое количество ссылок, для хранения ссылок на дочерние узлы естественно использовать связный список, а не массив. Пример такого представления приведен на рис. 5.22. Из этого примера видно, что каждый узел содержит две ссылки: одну для связного списка, соединяющего его с сестринскими узлами, и вторую для связного списка его дочерних узлов.
Представление упорядоченного дерева с помощью связного списка дочерних узлов каждого узла эквивалентно его представлению в виде двоичного дерева. На схеме справа вверху показано представление в виде связного списка дочерних узлов для дерева, показанного слева вверху. Этот список реализован в правых ссылках узлов, а левая ссылка каждого узла указывает на первый узел в связном списке его дочерних узлов. На схеме справа внизу приведена несколько измененная версия верхней схемы; она представляет бинарное дерево, изображенное слева внизу. Таким образом, бинарное дерево можно рассматривать в качестве представления обобщенного дерева.
Лемма 5.4. Существует взаимно однозначное соответствие между бинарными деревьями и упорядоченными лесами.
Это соответствие показано на
рис.
5.22. Любой лес можно представить в виде бинарного дерева, в котором левая ссылка каждого узла указывает на его левый дочерний узел, а правая ссылка каждого узла - на сестринский узел, расположенный справа. 
Определение 5.4. Дерево с корнем (или неупорядоченное дерево) - это узел (называемый корнем), связанный с мультимножеством деревьев с корнем. (Такое мультимножество называется неупорядоченным лесом.)
Деревья, с которыми мы встречались в "Введение" , посвященной задаче связности, являются неупорядоченными деревьями. Такие деревья могут быть определены как упорядоченные деревья, в которых порядок расположения дочерних узлов узла неважен. Неупорядоченные деревья можно определить и в виде множества отношений "роди -тельский -дочерний " между узлами. Может показаться, что этот вариант имеет слабое отношение к рассматриваемым рекурсивным структурам, но, возможно, такое конкретное представление наиболее соответствует абстрактному понятию дерева.
Неупорядоченное дерево можно представить в компьютере упорядоченным деревом; нужно лишь осознавать, что одно и то же неупорядоченное дерево может быть представлено несколькими различными упорядоченными деревьями. Хотя обратная задача - определение того, представляют ли два различные упорядоченные дерева одно и то же неупорядоченное дерево (задача изоморфизма деревьев) - подается решению с трудом.
Наиболее общим видом деревьев является дерево, в котором не выделен корневой узел. Например, этим свойством обладают остовные деревья, полученные в результате работы алгоритмов связности из "Введение" . Для правильного определения неупорядоченных деревьев без корня, т.е. свободных деревьев, потребуется начать с определения графов (graph). Определение 5.5. Граф - это множество узлов вместе с множеством ребер, которые соединяют пары отдельных узлов (причем любая пара узлов соединяется не более чем одним ребром).
Из любого узла можно перейти вдоль ребра до другого узла, от этого - к следующему и т.д. Последовательность ребер, ведущая от одного узла до другого, когда ни один узел не посещается дважды, называется простым путем (simple path). Граф является связным (connected), если для любой пары узлов существует связывающий их простой путь. Простой путь, у которого первый и последний узел совпадают, называется циклом (cycle).
Каждое дерево является графом, а какие же графы являются деревьями? Граф считается деревом, если он удовлетворяет любому из следующих четырех условий:
- Граф имеет N - 1 ребер и ни одного цикла.
- Граф имеет N - 1 ребер и является связным.
- Каждую пару вершин в графе соединяет только один простой путь.
- Граф является связным, но перестает быть таковым при удалении любого ребра.
Любое из этих условий - необходимое и достаточное условие для выполнения остальных трех. Формально для определения свободного дерева следует выбрать одно из них; но мы, отбросив формальности, считаем определением все условия вместе.
Свободное дерево представляется просто как коллекция ребер. Если представлять свободное дерево неупорядоченным, упорядоченным или даже бинарным деревом, то необходимо учитывать, что в общем случае существует множество различных способов представления любого свободного дерева.
Абстракция дерева используется часто, и рассмотренные в этом разделе различия важны, поскольку знание различных абстракций деревьев зачастую существенно влияет на выбор эффективного алгоритма и соответствующих структур данных для решения данной задачи. Бывает, что приходится работать непосредственно с конкретными представлениями деревьев без учета конкретной абстракции, но зачастую имеет смысл поработать с подходящей абстракцией дерева, а затем рассмотреть различные конкретные представления. В данной книге приведено множество примеров этого процесса.
Прежде чем вернуться к алгоритмам и реализациям, мы рассмотрим ряд основных математических свойств деревьев; эти свойства будут использоваться при разработке и анализе алгоритмов на деревьях.
Упражнения
5.56. Приведите представления свободного дерева, показанного на рис. 5.20, в форме дерева с корнем и бинарного дерева.
5.57. Определите количество различных способов представления свободного дерева, показанного на рис. 5.20, в форме упорядоченного дерева.
5.58. Нарисуйте три упорядоченных дерева, которые изоморфны упорядоченному дереву, показанному на рис. 5.20. Это значит, должна существовать возможность преобразования всех четырех деревьев одного в другое путем обмена дочерних узлов.
5.59. Допустим, деревья содержат элементы, для которых определена операция ==. Напишите рекурсивную программу, которая удаляет в бинарном дереве все листья, содержащие элементы, равные данному (см. программу 5.5).
5.60. Измените функцию вида "разделяй и властвуй " для поиска максимального элемента в массиве (программа 5.6), чтобы она делила массив на к частей, размер которых различался бы не более чем на 1, рекурсивно находила максимум в каждой части и возвращала наибольший из этих максимумов.
5.61. Нарисуйте 3 -арные и 4 -арные деревья для случаев к = 3 и к = 4 в рекурсивной конструкции, предложенной в упражнении 5.60, для массива, состоящего из 11 элементов (см. рис. 5.6).
5.62. Бинарные деревья эквивалентны двоичным строкам, в которых нулевых битов на 1 больше, чем единичных, при соблюдении дополнительного ограничения, что в любой позиции к количество нулевых битов слева от к не больше количества единичных битов слева от к. Бинарное дерево - это либо строка, состоящая только из нуля, либо две таких строки, объединенные вместе, которым предшествует 1. Нарисуйте бинарное дерево, соответствующее строке
1110010110001011000
5.63. Упорядоченные деревья эквивалентны согласованным строкам из пар круглых скобок: упорядоченное дерево - это либо пустая строка, либо последовательность упорядоченных деревьев, заключенных в круглые скобки. Нарисуйте упорядоченное дерево, соответствующее строке
( ( ( ) ( ( ) ( ) ) ( ) ) ( ( ) ( ) ( ) ) )
5.64. Напишите программу для определения того, представляют ли два массива N целых чисел от 0 до N - 1 изоморфные неупорядоченные деревья, если интерпретировать их (как в "Введение" ) как ссылки из родительских узлов на дочерние в дереве с узлами, пронумерованными от 0 до N - 1. То есть программа должна определять, существует ли способ изменения нумерации узлов в одном дереве, чтобы представление в виде массива одного дерева было идентичным представлению в виде массива другого дерева.
5.65. Напишите программу для определения того, являются ли два бинарных дерева изоморфными неупорядоченными деревьями.
5.66. Нарисуйте все упорядоченные деревья, которые могли бы представлять дерево, определенное набором ребер 0 -1, 1 -2, 1 -3, 1 -4, 4 -5.
5.67. Докажите, что если в связном графе, состоящем из N узлов, удаление любого ребра влечет за собой разъединение графа, то в нем N - 1 ребер и ни одного цикла.