|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Рекурсия и деревья
Во-первых, рекурсивная структура этого решения непосредственно обуславливает количество необходимых перемещений.
Лемма 5.2. Рекурсивный алгоритм "разделяй и властвуй " для задачи о ханойских башнях дает решение, приводящее к 2N - 1 перемещениям.
Как обычно, из кода немедленно следует, что количество перемещений удовлетворяет условию рекуррентности. В данном случае рекуррентная формула похожа на формулу 2.5:
TN = 2TN -1 + 1, при , T1 = 1.
, T1 = 1.
Предсказанный результат можно непосредственно проверить методом индукции: мы имеем T(1) = 21 - 1 = 1; и, если для к < N верно T(к) = 2k - 1, то T(N) = 2 (2N -1 - 1) + 1 = 2N - 1. 
Программа 5.7. Решение задачи о ханойских башнях
Чтобы переместить башню из дисков вправо, мы перемещаем (рекурсивно) все диски, кроме нижнего, влево, потом перекладываем нижний диск вправо, а затем перемещаем (рекурсивно) башню поверх нижнего диска.
void hanoi(int N, int d)
{
if (N == 0) return;
hanoi(N -1, -d);
shift(N, d);
hanoi(N -1, -d);
}
На этой схеме показано решение задачи о ханойских башнях с пятью дисками. Мы перемещаем четыре верхних диска влево на одну позицию (левый столбец), затем перекладываем диск 5 вправо, а затем верхние четыре диска перемещаем влево на одну позицию (правый столбец). Приведенная ниже последовательность вызовов функций образует вычисление для трех дисков. Вычисленная последовательность перемещений - +1 -2 +1 +3 +1 -2 +1 - появляется в решении четыре раза (для примера показаны первые семь перемещений).
Если монахи перекладывают по одному диску в секунду, то для завершения работы им потребуется, по меньшей мере, 348 столетий (см. рис. 2.1) - разумеется, если они не допускают ошибок. Скорее всего, конец света наступит даже позже этого срока, поскольку, по -видимому, монахи не пользуются программой 5.7 для быстрого выяснения, какой диск нужно переложить следующим. А теперь давайте проанализируем метод, который ведет к простому (не рекурсивному) решению, упрощающему принятие решения. Не хочется помогать монахам, однако этот метод имеет большое значение для множества практически важных алгоритмов.
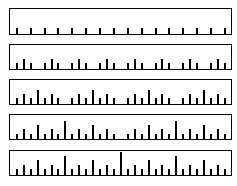
Чтобы понять решение задачи о ханойских башнях, рассмотрим простую задачу рисования меток на линейке. Каждые 1/2 дюйма на линейке отмечаются черточкой, каждые 1/4 дюйма отмечаются несколько более короткими черточками, 1/8 дюйма - еще более короткими и т.д. Задача состоит в создании программы для рисования этих меток для любого заданного разрешения, при условии, что в нашем распоряжении имеется процедура mark(x, h) для рисования метки высотой h условных единиц в позиции x.
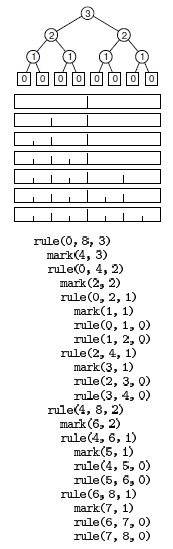
Если требуемое разрешение равно 1/2n дюйма, мы перейдем к другой задаче: поместить метки в каждой точке в интервале от 0 до 2n, за исключением конечных точек. Тогда средняя метка должна иметь высоту n единиц, метки в середине левой и правой половин должны иметь высоту n - 1 единиц и т.д. Программа 5.8 - простой алгоритм "разделяй и властвуй " для выполнения этой задачи; его работа на небольшом примере проиллюстрирована на рис. 5.8. Рекурсивный метод состоит в следующем. Для помещения меток на интервале он вначале делится на две равные половины. Затем создаются (рекурсивно) более короткие метки в левой половине, в середине помещается длинная метка, и создаются (рекурсивно) более короткие метки в правой половине. На рис. 5.8 видно, что с помощью этого метода метки создаются по порядку, слева направо (то есть итеративно) - и проблема заключается в вычислении длин меток. Дерево рекурсии, приведенное на рисунке, помогает понять вычисления: просматривая его сверху вниз, мы видим, что длина меток уменьшается на 1 для каждого рекурсивного вызова функции. Если просматривать дерево в поперечном направлении, мы получаем метки в порядке нанесения, поскольку для каждого данного узла вначале рисуются метки, связанные с вызовом функции слева, затем метка, связанная с данным узлом, а затем метки, связанные с вызовом функции справа.
Программа 5.8. Применение алгоритма "разделяй и властвуй " для рисования линейки
Для отрисовки меток на линейке мы рисуем метки в левой половине, затем самую длинную метку в середине, а затем метки в правой половине. Данная программа предназначена для использования со значением r - l, равным степени 2 - и это свойство сохраняется в ее рекурсивных вызовах (см. упражнение 5.27).
void rule(int l, int r, int h)
{ int m = (l+r)/2;
if (h > 0)
{
rule(l, m, h -1);
mark(m, h);
rule(m, r, h -1);
}
}
Cразу видно, что последовательность длин в точности совпадает с последовательностью перемещаемых дисков при решении задачи о ханойских башнях. Действительно, простым доказательством их идентичности является идентичность рекурсивных программ. То есть для определения перекладываемого диска наши монахи могли бы воспользоваться метками на линейке.
Более того, и решение задачи о ханойских башнях в программе 5.7, и программа рисования линейки в программе 5.8 являются вариантами общей схемы "разделяй и властвуй ", представленной программой 5.6. Все три программы решают задачу размера 2n, разбивая ее на две задачи размера 2n -1. При отыскании максимума время получения решения линейно зависит от размера входного массива; при рисовании линейки и при решении задачи о ханойских башнях время линейно зависит от размера выходного массива. Обычно считается, что время выполнения задачи о ханойских башнях экспоненциально, хотя объем задачи измеряется количеством дисков, т.е. п.
Эта последовательность вызовов функции вычисляет длины меток для рисования линейки длиной 8, в результате чего наносятся метки 1, 2, 1, 3, 1, 2 и 1.
Рисование меток на линейке с помощью рекурсивной программы не представляет особой сложности, но, может быть, существует более простой способ вычисления длины i -ой метки для любого данного значения i? На рис. 5.9 показан еще один простой вычислительный процесс, дающий ответ на этот вопрос. Оказывается, i -е число, выводимое и программой решения задачи о ханойских башнях, и программой рисования линейки - просто количество оконечных нулевых разрядов в двоичном представлении i. Это утверждение можно доказать методом индукции по соответствию с формулировкой метода "разделяй и властвуй " для процесса вывода таблицы " -разрядных чисел: достаточно напечатать таблицу (п - 1) -разрядных чисел, каждому из которых предшествует 0, а затем напечатать таблицу (п - 1) -разрядных чисел, каждому из которых предшествует 1 (см. упражнение 5.25).
Применительно к задаче о ханойских башнях соответствие n -разрядным числам дает простой алгоритм решения задачи. Можно переместить стопку дисков на один стержень вправо, повторяя до завершения следующие два шага:
- Перемещение маленького диска вправо, если п нечетно (влево, если четно).
- Выполнение единственного разрешенного перемещения, не затрагивающего маленький диск.
То есть после перекладывания маленького диска на остальных двух стержнях находятся сверху два диска, один из которых меньше другого.
Единственное разрешенное перемещение, не затрагивающее маленький диск - перемещение меньшего диска поверх большего. Каждое второе перемещение выполняется с маленьким диском по той же причине, по которой каждое второе число является нечетным, а каждая вторая метка на линейке является самой короткой. Вероятно, наши монахи знают этот секрет, поскольку трудно представить, как иначе они могли бы определять нужные перемещения.
Формальное доказательство методом индукции того, что в решении задачи о ханойских башнях каждое второе перемещение является перекладыванием маленького диска (им же все начинается и заканчивается), весьма поучительно: Для n = 1 существует только одно перемещение, затрагивающее маленький диск, следовательно, утверждение подтверждается. При n > 1 из предположения, что утверждение справедливо для n - 1, следует его справедливость и для n: первое решение для n - 1 начинается перекладыванием маленького диска, а второе решение для n - 1 завершается перекладыванием маленького диска - следовательно, решение для n начинается и завершается перекладыванием маленького диска. Перемещение, не затрагивающее маленький диск, вставляется между двумя перемещениями, которые его затрагивают (перекладыванием, завершающим первое решение для n - 1, и перекладыванием, начинающим второе решение для n - 1) - следовательно, свойство, что каждое второе перемещение является перекладыванием маленького диска, остается в силе.
Вычисление функции рисования линейки эквивалентно подсчету количества оконечных нулей в четных N -разрядных числах.
Программа 5.9 - альтернативный способ рисования линейки, на который натолкнуло соответствие с двоичными числами (см. рис. 5.10). Эту версию алгоритма называют восходящей (bottom -up) реализацией. Она не является рекурсивной, но определенно навеяна рекурсивным алгоритмом. Эта связь между алгоритмами "разделяй и властвуй " и двоичными представлениями чисел часто помогает найти решение при анализе и разработке усовершенствованных версий, таких как восходящие подходы. Мы будем рассматривать данную возможность, чтобы понять и, возможно, усовершенствовать каждый рассматриваемый алгоритм вида "разделяй и властвуй ".
Восходящий подход предполагает изменение порядка выполнения вычислений при рисовании линейки. На рис. 5.11 показан еще один пример, в котором изменен порядок следования трех вызовов функций в рекурсивной реализации. Этот пример соответствует рекурсивному рисованию первоначально описанным способом: нанесение средней метки, затем левой половины, а затем правой. Последовательность нанесения меток выглядит сложной, но является результатом простой перемены мест двух операторов в программе 5.8. Как будет показано в разделе 5.6, взаимосвязь между рис. 5.8 и рис. 5.11 сродни различию между постфиксными и префиксными арифметическими выражениями.
Программа 5.9. Нерекурсивная программа для рисования линейки
В отличие от программы 5.8, линейку можно нарисовать, вначале изобразив все метки длиной 1, затем все метки длиной 2 и т.д. Переменная t представляет длину меток, а переменная j - количество меток между двумя последовательными метками длиной t. Внешний цикл for увеличивает значение t при сохранении соотношения j = 2 -1. Внутренний цикл for рисует все метки длиной t.
void rule(int l, int r, int h)
{
for (int t = 1, j = 1; t <= h; j += j, t++)
for (int i = 0; l+j+i <= r; i += j+j)
mark(l+j+i, t);
}
Возможно, нанесение меток в порядке, показанном на рис. 5.8, более удобно по сравнению с вычислениями в измененном порядке, которые содержатся в программе 5.9 и приведены на рис. 5.11, поскольку в этом случае можно нарисовать линейку произвольной длины. Достаточно представить себе графическое устройство, которое просто непрерывно перемещается от одной метки к следующей. Аналогично, при решении задачи о ханойских башнях мы ограничены последовательностью перемещений, которая должна быть выполнена. Вообще говоря, многие рекурсивные программы основываются на решениях подзадач, которые должны быть выполнены в конкретном порядке. Для других вычислений (см., например, программу 5.6) порядок решения подзадач роли не играет. Для таких вычислений единственным ограничением служит необходимость решения подзадач перед тем, как можно будет решить главную задачу. Понимание того, когда можно изменять порядок вычисления, не только служит ключом к успешной разработке алгоритма, но и во многих случаях оказывает непосредственное практическое влияние. Например, этот вопрос исключительно важен при реализации алгоритмов для работы на параллельных процессорах.
Восходящий подход соответствует общему методу разработки алгоритмов, при котором задача решается путем решения вначале элементарных подзадач с последующим объединением этих решений для получения решения несколько больших подзадач и т.д., пока вся задача не будет решена. Этот подход можно было бы назвать "объединяй и властвуй ".
Лишь небольшой шаг отделяет рисование линеек от рисования двумерных узоров, похожих на показанный на рис. 5.12. Этот рисунок показывает, как простое рекурсивное описание может приводить к сложным на вид вычислениям (см. упражнение 5.30).
Для рисования линейки нерекурсивным методом вначале рисуются все метки длиной 1 и пропускаются позиции, затем рисуются метки длиной 2 и пропускаются остающиеся позиции, затем рисуются метки длиной 3 с пропуском остающихся позиций и т.д.
Эта последовательность отображает результат нанесения меток перед рекурсивными вызовами, а не между ними.
Этот фрактал - двумерная версия рис. 5.10. Очерченные квадраты на нижнем рисунке демонстрируют рекурсивную структуру вычисления.
Рекурсивно определенные геометрические узоры, наподобие показанного на рис. 5.12, иногда называют фракталами. При использовании более сложных примитивов рисования и более сложных рекурсивных функций (особенно рекурсивно определенных функций на вещественной оси и комплексной плоскости) можно получить поразительно разнообразные и сложные узоры. На рис. 5.13 приведен еще один пример - звезда Коха, которая определяется рекурсивно следующим образом: звезда Коха порядка 0 - простой выступ, показанный на рис. 4.3, а звезда Коха n -го порядка - это звезда Коха порядка п - 1, в которой каждый отрезок заменен звездой порядка 0 соответствующего размера.
Подобно решениям задач рисования линейки и ханойских башен, эти алгоритмы линейны по отношению к количеству шагов, но это количество связано экспоненциальной зависимостью с максимальной глубиной рекурсии (см. упражнения 5.29 и 5.33). Они также могут быть непосредственно связаны с последовательностью натуральных чисел в соответствующей системе счисления (см. упражнение 5.34).
Это изменение программы PostScript, приведенной на рис. 4.3, преобразует результат ее работы в фрактал (см. текст).
Задача о ханойских башнях, рисование линейки и фракталы весьма занимательны, а связь с двоичным числами поражает, однако все эти вопросы интересуют нас прежде всего потому, что облегчают понимание одного из основных методов разработки алгоритмов - деление задачи пополам и независимое решение одной или обеих половин задачи. Возможно, это наиболее важная из всех технологий, рассматриваемых в книге. В таблица 5.1 подробно описаны бинарный поиск и сортировка слиянием, которые не только являются важными и широко используемыми на практике алгоритмами, но и служат типичными примерами разработки алгоритмов вида "разделяй и властвуй ".
Бинарный поиск (см. "Принципы анализа алгоритмов" и "Таблицы символов и деревья бинарного поиска" ) и сортировка слиянием (см. "Слияние и сортировка слиянием" ) - типичные алгоритмы "разделяй и властвуй ", которые обеспечивают гарантированную оптимальную производительность, соответственно, поиска и сортировки. Рекуррентные соотношения демонстрируют сущность вычислений методом "разделяй и властвуй " для каждого алгоритма. (Вывод решений, приведенных в правом столбце, см. в разделах 2.5 "Принципы анализа алгоритмов" и 2.6.) При бинарном поиске задача делится пополам, выполняется одно сравнение, а затем рекурсивный вызов для одной из половин. При сортировке слиянием задача делится пополам, затем выполняется рекурсивная обработка обеих половин, после чего программа выполняет N сравнений. В книге будет рассмотрено множество других алгоритмов, разработанных с применением этих рекурсивных схем.
| рекуррентное соотношение | приближенное решение | |
|---|---|---|
| Бинарный поиск | ||
| количество сравнений | CN = CN/2 + 1 | lg N |
| Сортировка слиянием | ||
| количество рекурсивных вызовов | AN = 2AN/2 + 1 | N |
| количество сравнений | CN = 2CN/2 + N | NlgN |
Быстрая сортировка (см. "Быстрая сортировка" ) и поиск в бинарном дереве (см. "Таблицы символов и деревья бинарного поиска" ) представляют важную разновидность базового подхода "разделяй и властвуй ", в которой задача разбивается на подзадачи размеров k - 1 и N - k для некоторого k, определенного во входных данных. При случайных входных данных эти алгоритмы разбивают задачи на подзадачи, размеры которых в среднем вдвое меньше исходного (как в сортировке слиянием или бинарном поиске). Влияние этого различия будет рассмотрено при изучении этих алгоритмов.
Заслуживают внимания и следующие разновидности основной темы: разбиение на части различных размеров, разбиение более чем на две части, разбиение на перекрывающиеся части и выполнение различного объема вычислений в нерекурсивной части алгоритма. В общем случае алгоритмы "разделяй и властвуй " требуют выполнения вычислений для разбиения входного массива на части, либо для объединения результатов обработки двух независимо решенных частей исходной задачи, либо для упрощения задачи после того как половина входного массива обработана. То есть, код может находиться перед, после и между двумя рекурсивными вызовами. Естественно, подобные вариации приводят к созданию более сложных алгоритмов, чем бинарный поиск или сортировка слиянием, и эти алгоритмы труднее анализировать. В данной книге будут рассмотрены многочисленные примеры; к более сложным приложениям и способам анализа мы вернемся в части VIII.
Упражнения
5.16. Напишите рекурсивную программу, которая находит максимальный элемент в массиве, выполняя сравнение первого элемента с максимальным элементом остальной части массива (найденным рекурсивно).
5.17. Напишите рекурсивную программу, которая находит максимальный элемент в связном списке.
5.18 Измените программу "разделяй и властвуй " для отыскания максимального элемента в массиве (программа 5.6), чтобы она делила массив размера N на две части, одна из которых имеет размер k=2risN - 1, а вторая - N - к (чтобы размер хотя бы одной части был степенью 2).
5.19. Нарисуйте дерево, которое соответствует рекурсивным вызовам, выполняемым программой из упражнения 5.18 при размере массива 11.
5.20. Методом индукции докажите, что количество вызовов функции, выполняемых любым алгоритмом "разделяй и властвуй ", который делит задачу на части, в сумме составляющие задачу в целом, а затем решает части рекурсивно, линейно относительно размера задачи.
5.21. Докажите, что рекурсивное решение задачи о ханойских башнях (программа 5.7) является оптимальным. То есть покажите, что любое решение требует по меньшей мере 2N - 1 перекладываний.
5.22. Напишите рекурсивную программу, которая вычисляет длину i -ой метки на линейке с 2n - 1 метками.
5.23. Проанализируйте таблицы " -разрядных чисел наподобие приведенной на рис. 5.9 и определите свойство i -го числа, определяющего направление i -го перемещения (указанного знаковым битом на рис. 5.7) при решении задачи о ханойских башнях.
5.24. Напишите программу, которая выдает решение задачи о ханойских башнях путем заполнения массива, содержащего все перемещения, как сделано в программе 5.9.
5.25. Напишите рекурсивную программу, которая заполняет массив размером n х 2n нулями и единицами таким образом, чтобы массив представлял все n -разрядные числа, как показано на рис. 5.9.
5.26. Приведите результаты использования рекурсивной программы рисования линейки (программа 5.8) для следующих значений аргументов: rule(0, 11, 4) , rule(4, 20, 4) и rule(7, 30, 5).
5.27. Докажите следующее свойство программы рисования линейки (программа 5.8): если разность между ее первыми двумя аргументами является степенью 2, то оба ее рекурсивных вызова также обладают этим свойством.
5.28. Напишите функцию, которая эффективно вычисляет количество завершающих нулей в двоичном представлении целого числа.
5.29. Сколько квадратов изображено на рис. 5.12 (включая и те, которые скрыты большими квадратами)?
5.30. Напишите рекурсивную программу на C++, результатом которой будет PostScript -программа в форме списка вызовов функций x y r box, которая вычерчивает нижнюю диаграмму на рис. 5.12; функция box рисует квадрат rxr в точке с координатами (x, y). Реализуйте функцию box в виде команд PostScript (см. "Абстрактные типы данных" ).
5.31. Напишите восходящую нерекурсивную программу (аналогичную программе 5.9), которая вычерчивает верхнюю часть рис. 5.12 способом, описанным в упражнении 5.30.
5.32. Напишите PostScript -программу, вычерчивающую нижнюю часть рис. 5.12.
5.33. Сколько прямолинейных отрезков содержит звезда Коха " -го порядка?
5.34. Вычерчивание звезды Коха n -го порядка сводится к выполнению последовательности команд вида "повернуть на а градусов, затем прочертить отрезок длиной 1/3" ". Найдите связь с системами счисления, которая позволяет вычертить звезду путем увеличения значения счетчика и последующего вычисления угла а из этого значения.
5.35. Измените программу рисования звезды Коха, приведенную на рис. 5.13, для создания другого фрактала, на основе фигуры, состоящей из 5 линий нулевого порядка, вычерчиваемых смещениями на одну условную единицу в восточном, северном, восточном, южном и восточном направлениях (см. рис. 4.3).
5.36. Напишите рекурсивную функцию "разделяй и властвуй " для отображения аппроксимации прямолинейного отрезка в пространстве целочисленных координат для заданных конечных точек. Считайте, что все координаты имеют значения от 0 до M. Совет: вначале поставьте точку вблизи середины сегмента.