|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Рекурсия и деревья
Динамическое программирование
Основная характеристика алгоритмов вида "разделяй и властвуй ", рассмотренных в разделе 5.2 - разбиение ими задачи на независимые подзадачи. Если подзадачи не являются независимыми, ситуация усложняется, в первую очередь потому, что непосредственная рекурсивная реализация даже простейших алгоритмов этого типа может требовать неприемлемых затрат времени. В данном разделе рассматривается систематический подход, который позволяет избежать этой опасности в некоторых случаях.
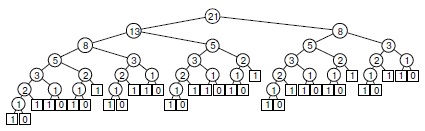
Например, программа 5.10 - непосредственная рекурсивная реализация рекуррентного соотношения, определяющего числа Фибоначчи (см. "Элементарные структуры данных" ). Не используйте эту программу - она весьма неэффективна. Действительно, количество рекурсивных вызовов для вычисления FN равно FN+1. Но FN приближенно равно фN, где ф " 1,618 - пропорция золотого сечения. Как это ни удивительно, но для программы 5.10 время этого элементарного вычисления определяется экспоненциальной зависимостью. На рис. 5.14, на котором приведены рекурсивные вызовы для небольшого примера, наглядно демонстрируется требуемый объем повторных вычислений.
Из схемы рекурсивных вызовов для вычисления F8 с помощью стандартного рекурсивного алгоритма видно, как рекурсия с перекрывающимися подзадачами может привести к экспоненциальному возрастанию затрат. В данном случае второй рекурсивный вызов игнорирует вычисление, выполненное во время первого вызова, что приводит к значительным повторным вычислениям, поскольку эффект нарастает в геометрической прогрессии. Рекурсивные вызовы для вычисления F6 = 8 (показаны в правом поддереве корня и в левом поддереве левого поддерева корня) приведены ниже.
И напротив, используя обычный массив, можно легко вычислить первые N чисел Фибоначчи за время, пропорциональное N:
F[0] = 0; F[1] = 1;
for (i = 2; i <= N; i++)
F[i] = F[i -1] + F[i -2];
Числа возрастают экспоненциально, поэтому массив не должен быть большим; например, F45 = 1836311903 - наибольшее число Фибоначчи, которое может быть представлено 32 -разрядным целым, поэтому достаточно использовать массив с 46 элементами.
Этот подход дает непосредственный способ получения численных решений для любых рекуррентных соотношений. В случае с числами Фибоначчи можно обойтись даже без массива и ограничиться только последними двумя значениями (см. упражнение 5.37); однако во многих других случаях часто встречающихся рекуррентных соотношений (см., например, упражнение 5.40) необходим массив для хранения всех известных значений.
Программа 5.10. Числа Фибоначчи (рекурсивная реализация)
Эта программа выглядит компактно и изящно, однако неприменима на практике, поскольку время вычисления FN экспоненциально зависит от N. Время вычисления FN+1 в ф " 1.6 раз больше времени вычисления FN. Например, поскольку ф9 > 60, если для вычисления Fn компьютеру требуется около секунды, то для вычисления FN+9 потребуется более минуты, а для вычисления FN+18 - более часа.
int F(int i)
{
if (i < 1) return 0;
if (i == 1) return 1;
return F(i -1) + F(i -2);
}
Рекуррентное соотношение - это рекурсивная функция с целочисленными значениями. Рассуждения, приведенные в предыдущем абзаце, подсказывают, что любую такую функцию можно вычислить, вычисляя все значения функции, начиная с наименьшего, и используя на каждом шаге ранее вычисленные значения для подсчета текущего значения. Эта техника называется восходящим динамическим программированием (bottom -up dynamic programming). Она применима к любому рекурсивному вычислению при условии, что есть возможность хранить все ранее вычисленные значения. Такая техника разработки алгоритмов успешно используется для решения широкого круга задач. Так что обратите внимание на эту простую технологию, которая может изменить время выполнения алгоритма с экспоненциального на линейное!
Нисходящее динамическое программирование (top -down dynamic programming) - еще более простая техника, которая позволяет автоматически выполнять рекурсивные функции при том же (или меньшем) количестве итераций, что и в восходящем динамическом программировании. При этом рекурсивная программа должна (заключительным действием) сохранять каждое вычисленное ей значение и (первым действием) проверять эти значения во избежание повторного вычисления любого из них. Программа 5.11 - результат механического преобразования программы 5.10, в которой нисходящее динамическое программирование позволило уменьшить время выполнения до линейного.
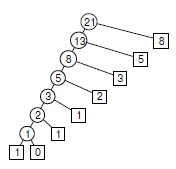
На рис. 5.15 демонстрируется радикальное уменьшение количества рекурсивных вызовов, достигнутое этим простым автоматическим изменением. Иногда нисходящее динамическое программирование называют также мемоизацией (memoization).
В качестве более сложного примера рассмотрим задачу о ранце: вор, грабящий сейф, находит в нем N видов предметов различных размеров и ценности, но имеет только небольшой ранец емкостью M, в котором может унести награбленное. Задача заключается в том, чтобы определить комбинацию предметов, которые вор должен уложить в ранец, чтобы общая стоимость похищенного оказалась наибольшей.
Программа 5.11. Числа Фибоначчи (динамическое программирование)
Сохранение вычисляемых значений в статическом массиве (элементы которого в C++ инициализируются 0) позволяет явно исключить любые повторные вычисления. Эта программа вычисляет Fn за время, пропорциональное N, что существенно отличается от времени 0(фN), которое требуется для вычислений программе 5.10.
int F(int i)
{ static int knownF[maxN];
if (knownF[i] != 0) return knownF[i];
int t = i;
if (i < 0) return 0;
if (i > 1) t = F(i -1) + F(i -2);
return knownF[i] = t;
}
Из этой схемы рекурсивных вызовов, выполненных для вычисления F 8 методом нисходящего динамического программирования, видно, как сохранение вычисленных значений снижает затраты с экспоненциального (см. рис. 5.14) до линейного.
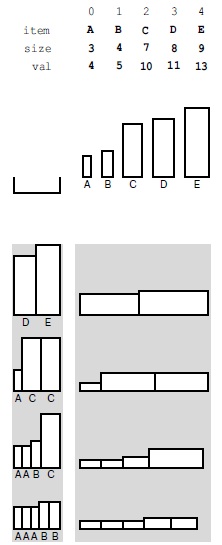
Входными данными задачи о ранце (вверху) являются емкость ранца и набор предметов различных размеров (которые представлены значениями на горизонтальной оси) и стоимости (значения на вертикальной оси). На этом рисунке показаны четыре различных способа заполнения ранца, размер которого равен 17; два из этих способов дают максимальную суммарную стоимость, равную 24.
Например, при наличии типов предметов, представленных на рис. 5.16, вор, располагающий ранцем, размер которого равен 17, может взять только пять (но не шесть) предметов A общей стоимостью 20, или предметы D и E суммарной стоимостью 24, или одно из множества других сочетаний. Наша цель - найти эффективный алгоритм для определения оптимального решения при любом заданном наборе предметов и вместимости ранца.
Решения задачи о ранце важны во многих приложениях. Например, транспортной компании может понадобиться определение наилучшего способа загрузки грузовика или транспортного самолета. В подобных приложениях могут встречаться и другие варианты этой задачи: например, может быть ограничено количество элементов каждого вида или могут быть доступны два грузовика. Многие из таких вариантов можно решить с помощью того же подхода, который будет рассмотрен ниже для решения только что сформулированной базовой задачи, однако бывают и гораздо более сложные варианты. Существует тонкая грань между решаемыми и нерешаемыми задачами этого типа, но об этом речь пойдет в части 8.
В рекурсивном решении задачи о ранце при каждом выборе предмета мы предполагаем, что можем (рекурсивно) определить оптимальный способ заполнения оставшегося места в ранце. Если объем ранца равен cap, то для каждого доступного элемента i определяется общая стоимость элементов, которые можно было бы унести, укладывая i -й элемент в ранец при оптимальной упаковке остальных элементов. Эта оптимальная упаковка - просто упаковка, которая определена (или будет определена) для меньшего ранца объемом cap -items[i].size. Здесь используется следующий принцип: оптимальные принятые решения в дальнейшем не требуют пересмотра. Когда установлено, как оптимально упаковать ранцы меньших размеров, эти задачи не требуют повторного исследования независимо от следующих элементов.
Программа 5.12 - прямое рекурсивное решение, которое основано на приведенных рассуждениях. Эта программа также неприменима для решения реальных задач, поскольку из -за большого объема повторных вычислений (см. рис. 5.17) время решения связано с количеством элементов экспоненциально. Но для решения задачи можно автоматически задействовать нисходящее динамическое программирование - и получить программу 5.13. Как и ранее, эта техника исключает все повторные вычисления (см. рис. 5.18).
Программа 5.12. Задача о ранце (рекурсивная реализация)
Как и в случае рекурсивного вычисления чисел Фибоначчи, не следует использовать эту программу, поскольку для ее выполнения потребуется экспоненциальное время и поэтому, возможно, не удастся получить решение даже небольшой задачи. Тем не менее, программа представляет компактное решение, которое легко можно усовершенствовать (см. программу 5.13). В ней предполагается, что элементы являются структурами с размером и стоимостью, которые определены как
typedef struct { int size; int val; } Item;
и имеется массив N элементов типа Item. Для каждого возможного элемента вычисляется (рекурсивно) максимальная стоимость, которую можно было бы получить, включив этот элемент в выборку, а затем выбирается максимальная из всех стоимостей.
int knap(int cap)
{ int i, space, max, t;
for (i = 0, max = 0; i < N; i++)
if ((space = cap -items[i].size) >= 0)
if ((t = knap(space) + items[i].val) > max)
max = t;
return max;
}
Программа 5.13. Задача о ранце (динамическое программирование)
Эта механическая модификация программы 5.12 снижает время выполнения с экспоненциального до линейного. Мы просто сохраняем любые вычисленные значения функции, а затем вместо выполнения рекурсивных вызовов выбираем сохраненные значения, когда они требуются (используя специальный признак для представления неизвестных значений). Индекс элемента сохраняется, поэтому при желании всегда можно восстановить содержимое ранца после вычисления: itemKnown[M] находится в ранце, остальное содержимое совпадает с оптимальной упаковкой ранца размера M -itemKnown[M]. size, следовательно, в ранце находится itemKnown[M -items[M].size] и т.д.
int knap(int M)
{ int i, space, max, maxi = 0, t;
if (maxKnown[M] != unknown) return maxKnown[M];
for (i = 0, max = 0; i < N; i++)
if ((space = M -items[i].size) >= 0)
if ((t = knap(space) + items[i].val) > max)
{ max = t; maxi = i; }
maxKnown[M] = max; itemKnown[M] = items[maxi];
return max;
}
Это дерево представляет структуру рекурсивных вызовов простого рекурсивного алгоритма решения задачи о ранце, реализованного в программе 5.12. Число в каждом узле означает оставшееся свободное место в ранце. Недостатком алгоритма является то же экспоненциальное время выполнения из -за большого объема повторных вычислений, требуемых для решения перекрывающихся подзадач, что и при вычислении чисел Фибоначчи (см. рис. 5.14).
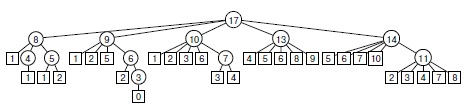
Рис. 5.18. Применение метода нисходящего динамического программирования для реализации алгоритма решения задачи о ранце
Как и в случае вычисления чисел Фибоначчи, техника сохранения известных значений уменьшает затраты алгоритма с экспоненциального (см. рис. 5.17) до линейного.
Динамическое программирование принципиально исключает все повторные вычисления в любой рекурсивной программе, при условии, что есть возможность хранить значения функции для аргументов, меньших аргумента текущего вызова.
Лемма 5.3. Динамическое программирование снижает время выполнения рекурсивной функции до не более чем суммарного времени, необходимого на вычисление функции для всех аргументов, меньших или равных данному аргументу, при условии, что затраты на рекурсивный вызов постоянны.
См. упражнение 5.50. 
Применительно к задаче о ранце из леммы следует, что время выполнения пропорционально произведению NM. Таким образом, задача о ранце легко поддается решению, когда емкость ранца не очень велика; для очень больших емкостей время и требуемый объем памяти могут оказаться недопустимо большими.
Восходящее динамическое программирование также применимо к задаче о ранце. Вообще -то метод восходящего программирования можно применять во всех случаях, когда применим метод нисходящего программирования, только при этом необходимо обеспечить вычисление значений функции в соответствующем порядке, чтобы каждое значение уже было вычислено, когда оно потребуется. Для функций, имеющих только один целочисленный аргумент, подобных рассмотренным, можно просто выполнять вычисления в порядке увеличения аргумента (см. упражнение 5.53), однако для более сложных рекурсивных функций определение правильного порядка может оказаться сложной задачей.
Например, совсем не обязательно ограничиваться рекурсивными функциями только с одним целочисленным аргументом. При наличии функции с несколькими целочисленными аргументами решения меньших подзадач можно сохранять в многомерных массивах, по одному измерению для каждого аргумента. В других ситуациях можно обойтись вообще без целочисленных аргументов и использовать абстрактную дискретную формулировку задачи, позволяющую разбить задачу на менее сложные. Примеры таких задач рассмотрены в частях V - VIII.
При использовании нисходящего динамического программирования известные значения сохраняются; при использовании восходящего динамического программирования они вычисляются заранее. В общем случае нисходящее динамическое программирование предпочтительней восходящего, поскольку
- оно представляет собой механическую трансформацию естественного решения задачи;
- порядок решения подзадач определяется сам собой;
- может не потребоваться решение всех подзадач.
Приложения, в которых применяется динамическое программирование, различаются по сущности подзадач и объему сохраняемой для них информации.
Однако необходимо учитывать следующий важный момент: динамическое программирование становится неэффективным, когда количество возможных значений функции, которые могут потребоваться, столь велико, что мы не можем себе позволить их сохранять (при нисходящем программировании) или вычислять предварительно (при восходящем программировании). Например, если в задаче о ранце объем ранца и размеры элементов - 64 -разрядные величины или числа с плавающей точкой, значения уже невозможно сохранять путем их индексирования в массиве. Это не просто небольшое неудобство, это принципиальная трудность. Для подобных задач пока не известно ни одного приемлемого решения; как будет показано в части 8, имеются веские причины считать, что эффективного решения нет вообще.
Динамическое программирование - это техника разработки алгоритмов, которая рассчитана в первую очередь на решение сложных задач того вида, который будет рассмотрен в частях V - VIII. Большинство алгоритмов, рассмотренных в частях II - IV, представляют собой реализацию методов "разделяй и властвуй " с не перекрывающимися подзадачами, и основное внимание было уделено скорее субквадратичной или сублинейной производительности, чем субэкспоненциальной. Однако нисходящее динамическое программирование является базовой техникой разработки эффективных реализаций рекурсивных алгоритмов, которая присутствует в арсенале средств любого, кто принимает участие в создании и реализации алгоритмов.