|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Рекурсия и деревья
Математические свойства бинарных деревьев
Прежде чем приступить к рассмотрению алгоритмов обработки деревьев, продолжим математическое исследование базовых свойств деревьев. Мы сосредоточим внимание на бинарных деревьях, поскольку они используются в книге чаще других. Понимание их основных свойств послужит фундаментом для понимания характеристик производительности различных алгоритмов, с которыми мы встретимся - не только тех, в которых бинарные деревья используются в качестве явных структур данных, но и рекурсивных алгоритмов "разделяй и властвуй ", и других аналогичных применений.
Лемма 5.5. Бинарное дерево с N внутренними узлами имеет N + 1 внешних узлов. Эта лемма доказывается методом индукции: бинарное дерево без внутренних узлов имеет один внешний узел, следовательно, для N = 0 лемма справедлива. Для N > 0 любое бинарное дерево с N внутренними узлами имеет к внутренних узлов в левом поддереве и N - 1 - к внутренних узлов в правом поддереве для некоторого к в диапазоне между 0 и N - 1, поскольку корень является внутренним узлом. В соответствии с индуктивным предположением левое поддерево имеет к + 1 внешних узлов, а правое поддерево - N - к внешних узлов, что в сумме составляет N + 1. ¦
Лемма 5.6. Бинарное дерево с N внутренними узлами имеет 2N ссылок: N - 1 ссылок на внутренние узлы и N + 1 ссылок на внешние узлы.
В любом дереве с корнем каждый узел, за исключением корня, имеет единственный родительский узел, и каждое ребро соединяет узел с его родительским узлом; следовательно, существует N - 1 ссылок, соединяющих внутренние узлы. Аналогично, каждый из N + 1 внешних узлов имеет одну ссылку на свой единственный родительский узел. 
Характеристики производительности многих алгоритмов зависят не только от количества узлов в связанных с ними деревьях, но и от различных структурных свойств.
Определение 5.6. Уровень (level) узла в дереве - число, на единицу большее уровня его родительского узла (корень размещается на уровне 0). Высота (height) дерева - максимальный из уровней узлов дерева. Длина пути (path length) дерева - сумма уровней всех узлов дерева. Длина внутреннего пути (internal path length) бинарного дерева - сумма уровней всех внутренних узлов дерева. Длина внешнего пути (external path length) бинарного дерева - сумма уровней всех внешних узлов дерева.
Удобный способ вычисления длины пути дерева заключается в суммировании произведений k на число узлов на уровне к для всех натуральных чисел k.
Для этих величин существуют также простые рекурсивные определения, вытекающие непосредственно из рекурсивных определений деревьев и бинарных деревьев. Например, высота дерева на 1 больше максимальной высоты поддеревьев его корня, а длина пути дерева с N узлами равна сумме длин путей поддеревьев его корня плюс N - 1. Приведенные величины также непосредственно связаны с анализом рекурсивных алгоритмов. Например, для многих рекурсивных вычислений высота соответствующего дерева в точности равна максимальной глубине рекурсии, то есть размеру стека, необходимого для поддержки вычисления.
Лемма 5.7. Длина внешнего пути любого бинарного дерева, имеющего N внутренних узлов, на 2N больше длины внутреннего пути.
Эту лемму можно было бы доказать методом индукции, но существует другое, более наглядное, доказательство (которое применимо и для доказательства леммы 5.6). Обратите внимание, что любое бинарное дерево может быть создано при помощи следующего процесса. Начинаем с бинарного дерева, состоящего из одного внешнего узла. Затем повторяем N раз следующее: выбираем внешний узел и заменяем его новым внутренним узлом с двумя дочерними внешними узлами. Если выбранный внешний узел находится на уровне к, длина внутреннего пути увеличивается на к, но длина внешнего пути увеличивается на к + 2 (удаляется один внешний узел на уровне к, но добавляются два на уровне к + 1). Этот процесс начинается с дерева, длина внутреннего и внешнего путей которого равны 0, и на каждом из N шагов длина внешнего пути увеличивается на 2 больше, чем длина внутреннего пути. 
Лемма 5.8. Высота бинарного дерева с N внутренними узлами не меньше lgN и не больше N - 1.
Худший случай - вырожденное дерево, имеющее только один лист и N - 1 ссылок от корня до этого листа (см. рис. 5.23). В лучшем случае мы имеем уравновешенное дерево с 2i внутренними узлами на каждом уровне i, за исключением самого нижнего (см. рис. 5.23). Если его высота равна h, то должно быть справедливо соотношение
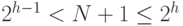
поскольку существует N + 1 внешних узлов. Из этого неравенства и следует данная лемма: в лучшем случае высота равна lgN, округленному до ближайшего целого числа. 
Лемма 5.9. Длина внутреннего пути бинарного дерева с N внутренними узлами не меньше чем N lg(N/ 4) и не превышает N(N - 1)/ 2.
Худший и лучший случай соответствуют тем же деревьям, которые упоминались при доказательстве леммы 5.8 и показаны на
рис.
5.23. В худшем случае длина внутреннего пути дерева равна 0 + 1 + 2 + ... + (N - 1) = N(N - 1)/2. В лучшем случае дерево имеет N + 1 внешних узлов при высоте, не превышающей 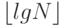 . Перемножив эти значения и применив лемму 5.7, получим предельное значение
. Перемножив эти значения и применив лемму 5.7, получим предельное значение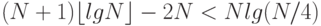 .
. 
Как мы увидим, бинарные деревья часто используются в компьютерных приложениях, и максимальная производительность достигается тогда, когда бинарные деревья полностью (или почти) сбалансированы. Например, деревья, которые использовались для описания алгоритмов "разделяй и властвуй ", подобных бинарному поиску и сортировке слиянием, полностью сбалансированы (см. упражнение 5.74).
В "Очереди с приоритетами и пирамидальная сортировка" и "Сбалансированные деревья" будут рассмотрены структуры данных, основанные на уравновешенных деревьях.
Эти основные свойства деревьев предоставляют информацию, необходимую для разработки эффективных алгоритмов решения многих практических задач. Более подробный анализ нескольких особых алгоритмов, с которыми придется встретиться, требует сложных математических выкладок, хотя часто полезные приближенные оценки можно получить с помощью простых индуктивных рассуждений, подобных использованным в этом разделе. В последующих главах мы продолжим рассмотрение математических свойств деревьев по мере возникновения необходимости. А пока можно вернуться к теме алгоритмов.
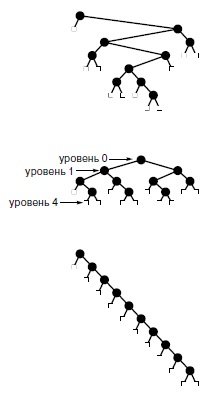
Бинарное дерево, показанное вверху, имеет высоту 7, длину внутреннего пути 31 и длину внешнего пути 51. Полностью сбалансированное бинарное дерево (в центре) с 10 внутренними узлами имеет высоту 4, длину внутреннего пути 19 и длину внешнего пути 39 (ни одно двоичное дерево с 10узлами не может иметь меньшее значение любого из этих параметров). Вырожденное дерево (внизу) с 10 внутренними узлами имеет высоту 10, длину внутреннего пути 45 и длину внешнего пути 65 (ни одно бинарное дерево с 10 узлами не может иметь большее значение любого из этих параметров).
Упражнения
5.68. Сколько внешних узлов существует в M -арном дереве с N внутренними узлами? Используйте свой ответ для определения объема памяти, необходимого для представления такого дерева, если считать, что каждая ссылка и каждый элемент занимает одно слово памяти.
5.69. Приведите верхнее и нижнее граничные значения высоты M -арного дерева с N внутренними узлами.
5.70. Приведите верхнее и нижнее граничные значения длины внутреннего пути M -арного дерева с N внутренними узлами.
5.71. Приведите верхнее и нижнее граничные значения количества листьев в бинарном дереве с N узлами.
5.72. Покажите, что если уровни внешних узлов в бинарном дереве различаются на константу, то высота дерева составляет O(logN).
5.73. Дерево Фибоначчи высотой n > 2 - это бинарное дерево с деревом Фибоначчи высотой n - 1 в одном поддереве и дерево Фибоначчи высотой n - 2 - в другом. Дерево Фибоначчи высотой 0 - это единственный внешний узел, а дерево Фибоначчи высотой 1 - единственный внутренний узел с двумя внешними дочерними узлами (см. рис. 5.14). Выразите высоту и длину внешнего пути для дерева Фибоначчи высотой n в виде функции от N (количество узлов в дереве).
5.74. Дерево вида "разделяй и властвуй ", состоящее из N узлов - это бинарное дерево с корнем, обозначенным N, деревом "разделяй и властвуй " из узлов в одном поддереве и деревом "разделяй и властвуй " из
узлов в одном поддереве и деревом "разделяй и властвуй " из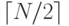 узлов в другом. (Дерево "разделяй и властвуй " показано на
рис.
5.6.) Нарисуйте дерево "разделяй и властвуй " с 11, 15, 16 и 23 узлами.
узлов в другом. (Дерево "разделяй и властвуй " показано на
рис.
5.6.) Нарисуйте дерево "разделяй и властвуй " с 11, 15, 16 и 23 узлами.
5.75. Докажите методом индукции, что длина внутреннего пути дерева вида "разделяй и властвуй " находится в пределах между N lgN и N lgN + N.
5.76. Дерево вида "объединяй и властвуй ", состоящее из N узлов - это бинарное дерево с корнем, обозначенным N, деревом "объединяй и властвуй " из узлов в одном поддереве и деревом "объединяй и властвуй " из
узлов в одном поддереве и деревом "объединяй и властвуй " из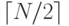 узлов в другом (см. упражнение 5.18). Нарисуйте дерево "объединяй и властвуй " с 11, 15, 16 и 23 узлами.
узлов в другом (см. упражнение 5.18). Нарисуйте дерево "объединяй и властвуй " с 11, 15, 16 и 23 узлами.
5.77. Докажите методом индукции, что длина внутреннего пути дерева вида "объединяй и властвуй " находится в пределах между N lgN и N lgN + N.
5.78. Полное (complete) бинарное дерево - это дерево, в котором заполнены все уровни, кроме, возможно, последнего, который заполняется слева направо, как показано на рис. 5.24. Докажите, что длина внутреннего пути полного дерева с N узлами лежит в пределах между N lgN и N lgN + N.
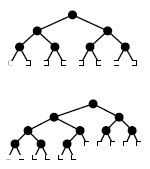
Если количество внешних узлов является степенью 2 (верхний рисунок), то все внешние узлы в полном бинарном дереве находятся на одном уровне. В противном случае (нижний рисунок) внешние узлы располагаются на двух уровнях, причем внутренние узлы находятся слева от внешних узлов предпоследнего уровня.