Контрпример
Лемма 1. Пусть 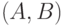 — непротиворечивая пара,
а
— непротиворечивая пара,
а  — произвольная формула. Тогда хотя бы одна из пар
— произвольная формула. Тогда хотя бы одна из пар 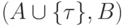 и
и 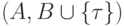 непротиворечива.
непротиворечива.
Доказательство леммы 1. Пусть обе пары с добавленным  противоречивы. Надо доказать, что противоречива исходная пара.
Другими словами, надо показать, что если в интуиционистском
исчислении высказываний выводимы формулы
противоречивы. Надо доказать, что противоречива исходная пара.
Другими словами, надо показать, что если в интуиционистском
исчислении высказываний выводимы формулы
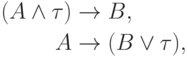
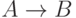 (для простоты мы отождествляем
множества
(для простоты мы отождествляем
множества  и
и  с конъюнкцией и дизъюнкцией их
элементов и считаем
с конъюнкцией и дизъюнкцией их
элементов и считаем  и
и  формулами).
формулами).В самом деле, по лемме о дедукции достаточно доказать, что  . Для этого достаточно установить, что
. Для этого достаточно установить, что
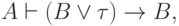
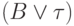 в предположении
в предположении  у нас уже
есть. Для этого, в свою очередь, достаточно установить, что
у нас уже
есть. Для этого, в свою очередь, достаточно установить, что 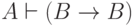 и
и 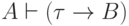 . Первое очевидно (и
посылка
. Первое очевидно (и
посылка  не нужна), второе равносильно выводимости формулы
не нужна), второе равносильно выводимости формулы 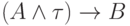 , которая нам дана по условию леммы. Лемма 1 доказана.
, которая нам дана по условию леммы. Лемма 1 доказана.Проведенное рассуждение, как говорят, устанавливает
допустимость (в интуиционистской логике) правила сечения,
позволяющего "иссечь" формулу  из формул
из формул 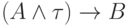 и
и 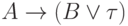 и получить
формулу
и получить
формулу 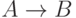 .
.
Возвращаясь к доказательству теоремы, рассмотрим произвольную
непротиворечивую пару 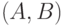 . Рассматривая по очереди различные
формулы
. Рассматривая по очереди различные
формулы  , мы будем добавлять их к левой или правой части.
Чтобы этот процесс ("пополнение") был конечным, мы ограничимся формулами из некоторого множества.
, мы будем добавлять их к левой или правой части.
Чтобы этот процесс ("пополнение") был конечным, мы ограничимся формулами из некоторого множества.
Фиксируем некоторое конечное множество формул  , которое
содержит все формулы из
, которое
содержит все формулы из  и замкнуто относительно перехода к
подформулам (если формула входит в
и замкнуто относительно перехода к
подформулам (если формула входит в  , то все ее подформулы
входят в
, то все ее подформулы
входят в  ). Например, можно включить в
). Например, можно включить в  все
подформулы всех формул из
все
подформулы всех формул из  и из
и из  .
.
Пару  , у которой
, у которой 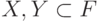 , будем
называть полной, если она непротиворечива и любая формула из
, будем
называть полной, если она непротиворечива и любая формула из  входит либо в
входит либо в  , либо в
, либо в  (то есть
(то есть 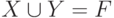 ). Заметим, что из непротиворечивости следует, что
). Заметим, что из непротиворечивости следует, что 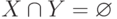 , так что полная пара задает разбиение
, так что полная пара задает разбиение  на
две части. (Более точно полные пары следовало бы называть
"полными относительно
на
две части. (Более точно полные пары следовало бы называть
"полными относительно  ", но у нас множество
", но у нас множество  фиксировано.)
фиксировано.)
Лемма 2. Исходная пара 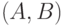 может быть расширена до
полной: существует полная пара
может быть расширена до
полной: существует полная пара  , для которой
, для которой 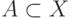 ,
, 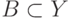 .
.
Доказательство очевидно: применяем по очереди лемму 1 ко всем
формулам из  .
.
Точно так же любую непротиворечивую пару, составленную из
формул множества  , можно расширить до полной. (Это замечание
нам впоследствии понадобится.)
, можно расширить до полной. (Это замечание
нам впоследствии понадобится.)
Для завершения доказательства теоремы 26.
нам осталось показать, что всякая полная пара 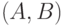 совместна
(существует шкала и мир, в котором формулы из
совместна
(существует шкала и мир, в котором формулы из  истинны, а
формулы из
истинны, а
формулы из  ложны). В отличие от классического случая построение
будет использовать не только пару
ложны). В отличие от классического случая построение
будет использовать не только пару 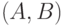 , но и все полные пары.
, но и все полные пары.
Шкала Крипке строится так. Мирами будут полные пары 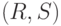 (то
есть всевозможные непротиворечивые разбиения множества
(то
есть всевозможные непротиворечивые разбиения множества  на
левую и правую части). Истинность переменных определяется
естественным образом: всякая переменная
на
левую и правую части). Истинность переменных определяется
естественным образом: всякая переменная  , входящая в одну из
формул множества
, входящая в одну из
формул множества  , сама принадлежит множеству
, сама принадлежит множеству  (замкнутость относительно подформул); если
(замкнутость относительно подформул); если  входит в левую
часть полной пары
входит в левую
часть полной пары 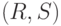 , то
, то  истинна в мире
истинна в мире 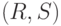 , если в
правую — то ложна. (Впоследствии это свойство мы распространим
на все формулы: любая формула из
, если в
правую — то ложна. (Впоследствии это свойство мы распространим
на все формулы: любая формула из  окажется истинной в мире
окажется истинной в мире 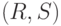 , а любая формула из
, а любая формула из  — ложной.)
— ложной.)
Осталось определить порядок на множестве пар. Считаем, что 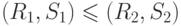 , если
, если  .
(Такое определение не удивительно, если вспомнить, что истинность
формул наследуется вверх.)
.
(Такое определение не удивительно, если вспомнить, что истинность
формул наследуется вверх.)
Лемма 3. В построенной шкале в мире 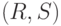 истинны все
формулы из
истинны все
формулы из  и ложны все формулы из
и ложны все формулы из  .
.
Доказательство леммы 3 проводится индукцией по построению
формул. Для переменных она верна по определению истинности.
Пусть некоторая формула из  не является переменной. Тогда
она есть конъюнкция, дизъюнкция, импликация или отрицание
и для ее частей утверждение леммы верно по предположению
индукции. Рассмотрим все случаи по очереди, начав с конъюнкции
и дизъюнкции (истинность которых не зависит от других миров).
не является переменной. Тогда
она есть конъюнкция, дизъюнкция, импликация или отрицание
и для ее частей утверждение леммы верно по предположению
индукции. Рассмотрим все случаи по очереди, начав с конъюнкции
и дизъюнкции (истинность которых не зависит от других миров).
( 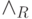 ) Пусть формула
) Пусть формула 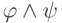 входит
в
входит
в  . Тогда формулы
. Тогда формулы  и
и  не могут входить в
не могут входить в  , иначе пара
, иначе пара 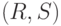 была бы противоречивой (из
была бы противоречивой (из 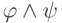 выводится
выводится  и
и  ). Значит,
). Значит,  и
и  входят
в
входят
в  (полнота), поэтому они истинны (предположение индукции),
и потому
(полнота), поэтому они истинны (предположение индукции),
и потому 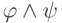 истинна (определение истинности).
истинна (определение истинности).
( 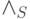 ) Пусть формула
) Пусть формула 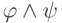 входит
в
входит
в  .
Могут ли обе формулы
.
Могут ли обе формулы  и
и  входить в
входить в  ? Нет, так
как в этом случае пара
? Нет, так
как в этом случае пара 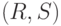 была бы противоречивой. Значит,
хотя бы одна из формул входит в
была бы противоречивой. Значит,
хотя бы одна из формул входит в  , тогда по предположению
индукции она ложна, и потому формула
, тогда по предположению
индукции она ложна, и потому формула 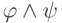 ложна в
мире
ложна в
мире 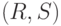 .
.
( 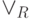 ) Если формула
) Если формула 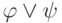 входит в
входит в  , то
формулы
, то
формулы  и
и  не могут одновременно входить
в
не могут одновременно входить
в  , и потому хотя бы одна из них истинна, так что и вся формула
, и потому хотя бы одна из них истинна, так что и вся формула 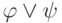 истинна.
истинна.
( 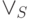 ) Если формула
) Если формула 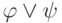 входит в
входит в  , то формулы
, то формулы  и
и  не могут входить в
не могут входить в  , поэтому обе они ложны и формула
, поэтому обе они ложны и формула 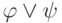 ложна.
ложна.
( 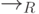 ) Пусть формула
) Пусть формула  входит в
входит в  . Проверим, что она истинна в
. Проверим, что она истинна в 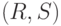 . Это значит, что в любом
мире
. Это значит, что в любом
мире 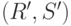 , который выше нашего (то есть
, который выше нашего (то есть 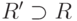 ) и в
котором истинна формула
) и в
котором истинна формула  , должна быть истинна и формула
, должна быть истинна и формула  . В самом деле, если
. В самом деле, если  истинна в
истинна в 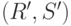 , то она входит в
, то она входит в 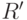 (предположение индукции). С другой стороны, и
(предположение индукции). С другой стороны, и  входит в
входит в 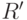 , поскольку
, поскольку 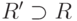 . Теперь ясно, что формула
. Теперь ясно, что формула  не может входить в
не может входить в 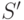 ,
так как в этом случае пара
,
так как в этом случае пара 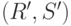 была бы противоречивой (из
была бы противоречивой (из  и
и  выводится
выводится  ). Значит,
). Значит,  входит в
входит в 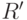 и потому истинна в
и потому истинна в 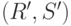 по
предположению индукции.
по
предположению индукции.
( 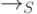 ) Это наиболее интересный случай, где нам снова
потребуется пополнение. Пусть формула
) Это наиболее интересный случай, где нам снова
потребуется пополнение. Пусть формула  входит
в
входит
в  . Мы должны доказать, что она ложна в мире
. Мы должны доказать, что она ложна в мире 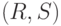 .
Согласно определению, это означает, что найдется мир
.
Согласно определению, это означает, что найдется мир 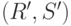 ,
для которого
,
для которого 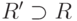 и в котором формула
и в котором формула  истинна, а формула
истинна, а формула  ложна (то есть
ложна (то есть  и
и  , согласно предположению индукции). Как найти такой
мир? Рассмотрим пару
, согласно предположению индукции). Как найти такой
мир? Рассмотрим пару 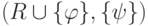 . Эта пара
непротиворечива. В самом деле, если бы формула
. Эта пара
непротиворечива. В самом деле, если бы формула 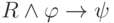 была бы выводима, то и формула
была бы выводима, то и формула 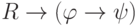 была бы выводима (лемма о дедукции), и
потому пара
была бы выводима (лемма о дедукции), и
потому пара 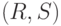 была бы противоречива. Теперь можно
расширить непротиворечивую пару
была бы противоречива. Теперь можно
расширить непротиворечивую пару 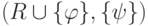 до полной пары
до полной пары 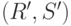 , которая и будет искомым миром.
, которая и будет искомым миром.
Отрицание рассматривается аналогично импликации (как мы уже
говорили, можно вместо отрицания ввести тождественную
ложь 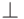 и вообще его не рассматривать).
и вообще его не рассматривать).
( 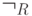 ) Пусть формула
) Пусть формула 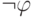 входит в
входит в  . Надо
доказать, что формула
. Надо
доказать, что формула  ложна в любом мире
ложна в любом мире 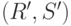 выше мира
выше мира 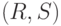 . Формула
. Формула  не может входить в
не может входить в 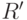 ,
так как в
,
так как в 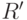 входит формула
входит формула  (напомним,
что
(напомним,
что 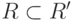 ), а из
), а из 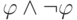 выводится любая формула. Значит,
выводится любая формула. Значит,  входит в
входит в 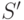 и по
индуктивному предположению формула
и по
индуктивному предположению формула  ложна в
ложна в 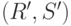 .
.
( 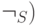 Пусть формула
Пусть формула  входит в
входит в  . В этом случае
пара
. В этом случае
пара 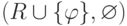 непротиворечива (если
из
непротиворечива (если
из  и
и  выводится противоречие, то из
выводится противоречие, то из  выводится
выводится  ). Расширив ее до полной, получаем высший мир
). Расширив ее до полной, получаем высший мир 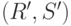 , в котором формула
, в котором формула  истинна (по
индуктивному предположению). Следовательно, формула
истинна (по
индуктивному предположению). Следовательно, формула  ложна в
мире
ложна в
мире 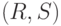 .
.
Лемма 3 доказана. Она завершает доказательство
теоремы 26. Напомним еще раз его схему.
Пусть формула  не выводима в интуиционистском
исчислении высказываний. Тогда пара
не выводима в интуиционистском
исчислении высказываний. Тогда пара 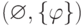 непротиворечива. Фиксируем множество
непротиворечива. Фиксируем множество  всех подформул формулы
всех подформул формулы  . Расширим нашу непротиворечивую пару до полной
(относительно
. Расширим нашу непротиворечивую пару до полной
(относительно  ). Эта полная пара будет одним из миров шкалы
Крипке (в которой мирами являются полные пары). Именно в этом
мире и будет ложной формула
). Эта полная пара будет одним из миров шкалы
Крипке (в которой мирами являются полные пары). Именно в этом
мире и будет ложной формула  .
.
36. Покажите, что если формулы  и
и  ложны в некоторых
мирах некоторых шкал Крипке, то можно построить шкалу Крипке и мир в ней,
для которого формула
ложны в некоторых
мирах некоторых шкал Крипке, то можно построить шкалу Крипке и мир в ней,
для которого формула 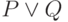 будет ложной.
(Указание: соединим шкалы, в которых ложны формулы
будет ложной.
(Указание: соединим шкалы, в которых ложны формулы  и
и  , в одну, добавив новый мир, который меньше миров, где
, в одну, добавив новый мир, который меньше миров, где  и
и  ложны.)
ложны.)
Из этой задачи и из теоремы о полноте вытекает такое следствие:
если дизъюнкция двух формул выводима в интуиционистском
исчислении высказываний, то хотя бы одна из формул тоже
выводима. Это свойство выполнено для многих интуиционистских
исчислений и соответствует начальной идее: доказать 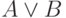 означает доказать одну из формул
означает доказать одну из формул  или
или  . Подобные
свойства можно доказывать и синтаксически, используя генценовские
варианты интуиционистских исчислений.
. Подобные
свойства можно доказывать и синтаксически, используя генценовские
варианты интуиционистских исчислений.
37. (а) Покажите, что формула 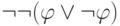 выводима в интуиционистском исчислении высказываний. (б)
Покажите, что если формулы
выводима в интуиционистском исчислении высказываний. (б)
Покажите, что если формулы  и
и  выводимы в интуиционистском исчислении высказываний, то и формула
выводимы в интуиционистском исчислении высказываний, то и формула 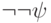 выводима в интуиционистском исчислении
высказываний. (в) Докажите, что если формула
выводима в интуиционистском исчислении
высказываний. (в) Докажите, что если формула  выводима в классическом
исчислении высказываний, то формула
выводима в классическом
исчислении высказываний, то формула  выводима
в интуиционистском исчислении высказываний (теорема Гливенко)
(г) Покажите, что для формул, содержащих лишь конъюнкцию и отрицание,
разницы между классическим и интуиционистским исчислениями нет:
из классической выводимости следует интуиционистская (теорема Геделя).
выводима
в интуиционистском исчислении высказываний (теорема Гливенко)
(г) Покажите, что для формул, содержащих лишь конъюнкцию и отрицание,
разницы между классическим и интуиционистским исчислениями нет:
из классической выводимости следует интуиционистская (теорема Геделя).
Покажите, что интуиционистское исчисление высказываний разрешимо: существует алгоритм, который по произвольной формуле определяет, выводима ли она в интуиционистском исчислении высказываний. (Указание: оцените мощность контрмодели Крипке; можно обойтись и без этого, заметив, что и множество выводимых формул, и множество формул, имеющих конечные контрмодели, перечислимы.)
