Контрпример
31. Провести подробно доказательство выводимости в интуиционистском исчислении высказываний всех перечисленных формул.
С другой стороны, многие законы классической логики перестают быть выводимыми без закона исключенного третьего. Таковы, например, формулы
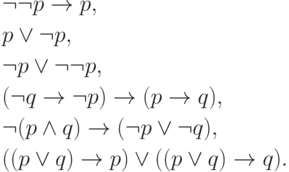
 и
и  , а не произвольные
формулы, поскольку результат подстановки некоторых формул вместо
, а не произвольные
формулы, поскольку результат подстановки некоторых формул вместо  и
и  может быть выводимой формулой. Например, если вместо
может быть выводимой формулой. Например, если вместо  в первую из перечисленных формул подставить формулу
в первую из перечисленных формул подставить формулу  , то
получится выводимая формула
, то
получится выводимая формула 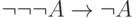 .
.Довольно ясно, что эти формулы не согласуются с интуиционистским
подходом. Например, в предпоследней формуле говорится, что если
мы опровергли предположение 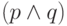 , то мы можем указать
на одно из предположений
, то мы можем указать
на одно из предположений  и
и  и предъявить его
опровержение. Вряд ли такой переход можно считать обоснованным с
интуиционистской точки зрения. Но, разумеется, формальный вопрос
о выводимости требует формального ответа.
и предъявить его
опровержение. Вряд ли такой переход можно считать обоснованным с
интуиционистской точки зрения. Но, разумеется, формальный вопрос
о выводимости требует формального ответа.
Начнем с закона исключенного третьего.
Теорема 24.Формула 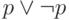 не выводима в интуиционистской логике.
не выводима в интуиционистской логике.
В классической логике каждая пропозициональная переменная может
принимать два значения — истина ( И ) и ложь ( Л ). В зависимости
от значений переменных каждой формуле также приписывается
значение И или Л. Расширим множество истинностных значений,
добавив новое значение Н (если угодно, можно считать это
сокращением слова "неизвестно"). Мы отождествляли И с
единицей, а Л — с нулем, так что логично отождествить Н с
числом 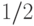 .
.
Мы докажем, что интуиционистски выводимые формулы всегда
принимают значение И, а формула 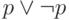 не такова, и
потому не выводима.
не такова, и
потому не выводима.
Чтобы определить значения формул в
трехзначной логике, необходимо задать таблицы истинности
для всех пропозициональных связок. Конъюнкцию определим как
минимум из двух значений (так что, например, 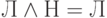 ,
а
,
а 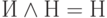 ), а дизъюнкцию — как максимум. Отрицание
действует так:
), а дизъюнкцию — как максимум. Отрицание
действует так:  ,
, 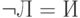 ,
, 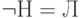 . (Последнее может показаться странным: почему бы не считать, что
. (Последнее может показаться странным: почему бы не считать, что 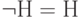 ? Оказывается, так нельзя — например, потому, что
тогда формула
? Оказывается, так нельзя — например, потому, что
тогда формула 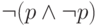 , которая выводима в
интуиционистской логике, будет иметь значение
, которая выводима в
интуиционистской логике, будет иметь значение  при
при 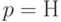 .)
.)
Сложнее всего определение истинности для импликации. Мы полагаем, что
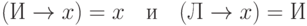
 , а также что
, а также что
Назовем формулу  -тавтологией,
если она принимает значение И при любых значениях переменных из множества
-тавтологией,
если она принимает значение И при любых значениях переменных из множества  . Теперь надо проверить две вещи: (1) все аксиомы
интуиционистского исчисления являются
. Теперь надо проверить две вещи: (1) все аксиомы
интуиционистского исчисления являются  -тавтологиями; (2)
если посылка импликации и вся импликация являются
-тавтологиями; (2)
если посылка импликации и вся импликация являются  -
тавтологиями, то и заключение тоже является
-
тавтологиями, то и заключение тоже является  -тавтологией.
Второе сразу ясно из определения импликации, а первое надо
аккуратно проверять, составив таблицы для всех аксиом. Мы не
будем этого подробно делать, поскольку это чисто механическая
проверка и поскольку чуть позже мы сможем вывести это из более
общего утверждения.
-тавтологией.
Второе сразу ясно из определения импликации, а первое надо
аккуратно проверять, составив таблицы для всех аксиом. Мы не
будем этого подробно делать, поскольку это чисто механическая
проверка и поскольку чуть позже мы сможем вывести это из более
общего утверждения.
Следовательно, всякая интуиционистски выводимая формула является  -тавтологией. Теперь заметим, что формула
-тавтологией. Теперь заметим, что формула 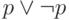 принимает значение Н при
принимает значение Н при 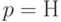 и потому не является
и потому не является  -тавтологией — значит, невыводима.
-тавтологией — значит, невыводима.
32. Покажите, что всякая  -тавтология является тавтологией
в обычном смысле.
-тавтология является тавтологией
в обычном смысле.
Использованный нами прием годится не всегда. Например,
интуиционистски невыводимая формула 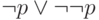 является
является  -тавтологией, поскольку (согласно нашему
определению) формула
-тавтологией, поскольку (согласно нашему
определению) формула 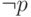 может принимать только значения И и Л.
может принимать только значения И и Л.
33. Какие из перечисленных нами интуиционистски невыводимых
формул являются  -тавтологиями?
-тавтологиями?
Более общий способ установления недоказуемости (невыводимости) различных формул доставляют шкалы Крипке (или модели Крипке, как еще говорят).
Чтобы задать шкалу Крипке, нужно:
- указать частично упорядоченное множество
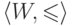 ,
называемое множеством миров;
,
называемое множеством миров; - для каждого мира указать, какие из пропозициональных переменных
считаются истинными в этом мире (остальные переменные считаются
ложными в этом мире). Если переменная
 истинна в
мире
истинна в
мире  , мы пишем
, мы пишем 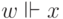 .
.
При этом требуется, чтобы было выполнено следующее: если  и
и 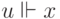 , то
, то 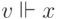 (область
истинности любой переменной наследственна вверх).
(область
истинности любой переменной наследственна вверх).
Когда шкала задана, можно определить истинность любой формулы (в
данном мире) индукцией по построению формулы. Мы пишем 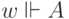 , если в мире
, если в мире  истинна формула
истинна формула  . Вот
индуктивное определение:
. Вот
индуктивное определение:
-
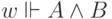 , если
, если 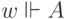 и
и 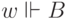 ;
; -
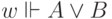 , если
, если 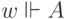 или
или 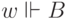 ;
; -
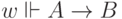 , если в любом мире
, если в любом мире  , в
котором истинна формула
, в
котором истинна формула  , истинна также и формула
, истинна также и формула  ;
; -
 , если ни в каком мире
, если ни в каком мире  формула
формула  не является истинной.
не является истинной.
Формула, не являющаяся истинной (в данном мире), называется ложной (в нем).
Определение истинности для отрицания, как легко проверить,
согласовано с пониманием  как
как 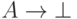 , где
, где 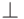 — тождественно ложная (во всех мирах) формула.
— тождественно ложная (во всех мирах) формула.
Именно определение импликации (и отрицания) использует порядок на множестве миров. Если формула содержит лишь конъюнкции и дизъюнкции, то ее истинность по существу определяется отдельно в каждом мире.
Индукцией по построению формулы  легко проверить, что если
она истинна в каком-то мире, то истинна и во всех больших
мирах. В самом деле, пересечение и объединение двух
наследственных вверх множеств также обладает этим свойством, так
что для случая конъюнкции и дизъюнкции можно сослаться на
предположение индукции. А для импликации даже и этого не нужно,
достаточно посмотреть на определение.
легко проверить, что если
она истинна в каком-то мире, то истинна и во всех больших
мирах. В самом деле, пересечение и объединение двух
наследственных вверх множеств также обладает этим свойством, так
что для случая конъюнкции и дизъюнкции можно сослаться на
предположение индукции. А для импликации даже и этого не нужно,
достаточно посмотреть на определение.
Философский смысл шкал Крипке иногда объясняют так. Пусть  есть множество возможных состояний цивилизации (миров);
есть множество возможных состояний цивилизации (миров);  означает, что мир
означает, что мир  может получиться из мира
может получиться из мира  в
результате развития цивилизации. Утверждение
в
результате развития цивилизации. Утверждение 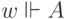 означает, что в
мире
означает, что в
мире  установлено, что высказывание
установлено, что высказывание  истинно. (При
этом оно останется истинным и при дальнейшем развитии цивилизации.)
Истинность
истинно. (При
этом оно останется истинным и при дальнейшем развитии цивилизации.)
Истинность  в мире
в мире  означает, что ни при
каком развитии цивилизации из состояния
означает, что ни при
каком развитии цивилизации из состояния  высказывание
высказывание  не станет истинным.
не станет истинным.
Определение истинности отрицания в шкалах Крипке предвосхитил
Пушкин, когда писал "нет правды на земле. Но правды нет и
выше,  " (Моцарт и Сальери).
" (Моцарт и Сальери).
34.Во что превращается определение истинности в шкале Крипке, если в ней только один мир? если в ней никакие два мира не сравнимы?
