Контрпример
Теорема 25 (корректность интуиционистского исчисления высказываний относительно шкал Крипке). Формула, выводимая в интуиционистском исчислении высказываний, истинна во всех мирах всех шкал Крипке.
Надо проверить, что все аксиомы истинны во всех мирах,
а также что правило modus ponens сохраняет это свойство.
Второе очевидно: если 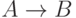 истинна во всех мирах и
истинна во всех мирах и  истинна во всех мирах, то по определению истинности импликации
истинна во всех мирах, то по определению истинности импликации  будет истинна во всех мирах.
будет истинна во всех мирах.
Осталось проверить истинность всех аксиом. Чтобы установить,
что импликация  истинна во всех мирах,
надо проверить, что в тех мирах, где истинна формула
истинна во всех мирах,
надо проверить, что в тех мирах, где истинна формула  ,
истинна и формула
,
истинна и формула  . Для первой аксиомы
. Для первой аксиомы 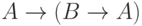 : если формула
: если формула  истинна в некотором мире, то в силу монотонности
она истинна и выше, так что
истинна в некотором мире, то в силу монотонности
она истинна и выше, так что  также истинна.
также истинна.
Проверим вторую аксиому 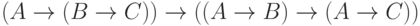 . Пусть
. Пусть 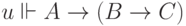 . Надо
убедиться, что
. Надо
убедиться, что 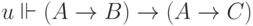 . Это
означает, что если
. Это
означает, что если  и
и 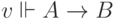 , то
, то 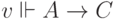 . Последнее, в свою очередь, значит, что если
. Последнее, в свою очередь, значит, что если 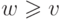 и
и 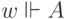 , то
, то 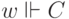 . Но в силу монотонности мы
знаем, что
. Но в силу монотонности мы
знаем, что 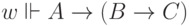 и
и 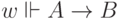 .
Поэтому из
.
Поэтому из 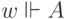 следует
следует 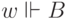 ,
, 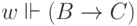 , и, наконец,
, и, наконец, 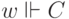 , что и требовалось.
, что и требовалось.
Остальные аксиомы проверяются еще проще.
Таким образом, чтобы доказать, что некоторая формула не выводима в интуиционистском исчислении высказываний, достаточно предъявить шкалу Крипке, в одном из миров которой она ложна.
35. Покажите, что в этом случае есть шкала, в которой среди миров есть наименьший и в нем формула ложна.
Для формулы 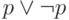 такая шкала строится легко. Возьмем
два мира, первый меньше второго. Пусть
такая шкала строится легко. Возьмем
два мира, первый меньше второго. Пусть  истинна только во
втором мире. Тогда
истинна только во
втором мире. Тогда 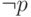 не будет истинна нигде, а
не будет истинна нигде, а 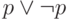 будет истинна только во втором мире.
будет истинна только во втором мире.
На самом деле это доказательство в сущности совпадает с приведенным выше (с трехзначной логикой). В самом деле, в этой шкале для формулы есть три возможности: она истинна в обоих мирах, она истинна только во втором мире, или она не истинна ни в одном из миров. Эти три возможности соответствуют трем значениям И, Н и Л в рассмотренной нами трехзначной интерпретации. Легко проверить, что таблицы операций как раз соответствуют определению истинности в модели Крипке.
Теперь мы можем установить, что все перечисленные выше формулы
невыводимы в интуиционистском исчислении высказываний. Для
формулы 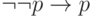 годится та же самая шкала
(
годится та же самая шкала
(  истинно только в большем мире). Она же годится для формулы
истинно только в большем мире). Она же годится для формулы 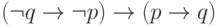 , если
, если  истинно в
обоих мирах, а
истинно в
обоих мирах, а  — только в большем. Для трех оставшихся формул
можно рассмотреть шкалы с тремя мирами: начальным миром
— только в большем. Для трех оставшихся формул
можно рассмотреть шкалы с тремя мирами: начальным миром  , из
которого можно попасть в
, из
которого можно попасть в  и в
и в 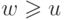 ; миры
; миры  и
и  не сравнимы. Если формула
не сравнимы. Если формула  истинна только в мире
истинна только в мире  , то
формула
, то
формула 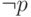 истинна только в мире
истинна только в мире  , a
, a  истинна только в мире
истинна только в мире  , так что в мире
, так что в мире  обе формулы
обе формулы 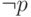 и
и  ложны и дизъюнкция
ложны и дизъюнкция 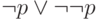 ложна. Чтобы построить контрмодель для формулы
ложна. Чтобы построить контрмодель для формулы 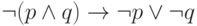 , будем считать, что
, будем считать, что  истинна
только в мире
истинна
только в мире  , а
, а  истинна только в мире
истинна только в мире  . Та же шкала годится и для формулы
. Та же шкала годится и для формулы  .
.
Оказывается, что этот прием универсален, как показывает следующая теорема.
Теорема 26 (полноты интуиционистского исчисления высказываний относительно шкал Крипке).
Для любой невыводимой в интуиционистском исчислении формулы  можно подобрать шкалу Крипке, в которой
можно подобрать шкалу Крипке, в которой  ложна в некотором мире.
ложна в некотором мире.
Напомним схему доказательства полноты классического исчисления
высказываний, приведенного в
разделе "Второе доказательство теоремы о полноте". Пусть
формула  невыводима. Мы хотим найти значения переменных, при которых
формула
невыводима. Мы хотим найти значения переменных, при которых
формула  ложна, то есть формула
ложна, то есть формула  истинна. Само по себе требование истинности
истинна. Само по себе требование истинности  не определяет
значения переменных однозначно. Чтобы избавиться от произвола,
мы расширяем непротиворечивое множество
не определяет
значения переменных однозначно. Чтобы избавиться от произвола,
мы расширяем непротиворечивое множество  до
полного множества
до
полного множества  и объявляем истинными те переменные,
которые входят в
и объявляем истинными те переменные,
которые входят в  .
.
Для интуиционистского случая в этой схеме требуются некоторые
изменения. Раньше ложность формулы  была равносильна
истинности формулы
была равносильна
истинности формулы  . В шкалах Крипке это уже не
так, и мы будем отдельно говорить об истинных и ложных (не истинных) формулах.
. В шкалах Крипке это уже не
так, и мы будем отдельно говорить об истинных и ложных (не истинных) формулах.
Пусть  и
и  — конечные множества
пропозициональных формул. Будем говорить, что пара
— конечные множества
пропозициональных формул. Будем говорить, что пара 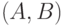 совместна,
если существует шкала Крипке и ее мир, в котором все формулы из
совместна,
если существует шкала Крипке и ее мир, в котором все формулы из  истинны, а все формулы из
истинны, а все формулы из  ложны. Будем говорить, что пара
ложны. Будем говорить, что пара 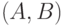 противоречива, если в интуиционистском исчислении
высказываний выводима формула
противоречива, если в интуиционистском исчислении
высказываний выводима формула
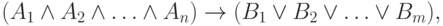
 — формулы множества
— формулы множества  , а
, а 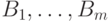 — формулы множества
— формулы множества  . (Без ограничения общности можно считать,
что перечислены все формулы множеств
. (Без ограничения общности можно считать,
что перечислены все формулы множеств  и
и  , поскольку
пропущенные формулы можно добавить, не нарушив выводимость.)
, поскольку
пропущенные формулы можно добавить, не нарушив выводимость.)Пример: если одна и та же формула входит в обе части пары, то такая пара противоречива.
Легко проверить, что противоречивая пара не может быть
совместна. В самом деле, если в некотором мире все формулы из  истинны, а все формулы из
истинны, а все формулы из  ложны, то посылка
импликации в этом мире истинна, а заключение ложно. Поэтому импликация ложна,
что противоречит ее выводимости (теорема о корректности).
ложны, то посылка
импликации в этом мире истинна, а заключение ложно. Поэтому импликация ложна,
что противоречит ее выводимости (теорема о корректности).
Мы докажем, что верно и обратное: всякая непротиворечивая пара
совместна. В частности, когда  состоит из единственной
формулы, получается утверждение теоремы о полноте. (Мы
предполагаем, как это обычно делается, что конъюнкция пустого
множества формул есть тождественно истинная формула, а
дизъюнкция — тождественно ложная. Поэтому противоречивость пары
состоит из единственной
формулы, получается утверждение теоремы о полноте. (Мы
предполагаем, как это обычно делается, что конъюнкция пустого
множества формул есть тождественно истинная формула, а
дизъюнкция — тождественно ложная. Поэтому противоречивость пары 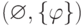 означает выводимость формулы
означает выводимость формулы  . Заметим кстати, что противоречивость пары
. Заметим кстати, что противоречивость пары 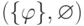 означает выводимость
формулы
означает выводимость
формулы  .)
.)
Итак, пусть имеется непротиворечивая пара 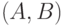 . Как доказать
ее совместность? Как и в классическом случае, мы устраним
произвол, расширив
. Как доказать
ее совместность? Как и в классическом случае, мы устраним
произвол, расширив  и
и  . Основным средством здесь
является такая лемма.
. Основным средством здесь
является такая лемма.
