Перспективные нейросетевые технологии

16.6. Графический диспетчер движения поездов

Ранее мы рассмотрели замечательную железнодорожную игру, основанную на современных воспитательных ценностях катастроф и насилий. Ну а серьезно?

Традиционно, расписание движения поездов через перегон, контролируемый одним диспетчером, составляется графически (рис. 16.7), в виде "картинки" с подразумеваемой системой координат. Горизонтально – время, вертикально – расстояние от одного крайнего пункта до другого, с указанием промежуточных. Тогда график движения каждого поезда – наклонная линия, с переменным углом наклона, с учетом остановок. Общий угол наклона линии соответствует направлению движения поезда через перегон. Несколько поездов, следующих через перегон, порождают сложную "картинку" их обслуживания с учетом приоритета (литера), возможного схождения путей в один, длины поезда (с учетом длины путей станций), необходимой скорости следования, запрета остановок.

Диспетчер должен уметь "развести" все поезда так, чтобы за счет ожиданий одних поездов на пунктах перегона провести другие поезда, выдержав приоритет: скорый, пассажирский, сквозной, сборный и т.д., – по возможности избежав столкновений и остановок вне раздельных пунктов.

На рисунке показан график движения поездов на однопутном перегоне. Здесь кривая 1 соответствует скорому поезду, кривые 2 и 3 – двум сквозным поездам. Эти три поезда следуют в одном направлении, из пункта А перегона. Кривая 4 соответствует сборному поезду, следующему в противоположном направлении из пункта В.

Составление расписания – оптимизационная задача (оптимизируются известные технико-экономические показатели) значительной трудоемкости. Поэтому до сих пор диспетчер фактически работает "вручную", хотя разработаны некоторые эвристические алгоритмы. Можно представить себе мастерство, интуицию и опыт диспетчера, демонстрирующего действительное искусство.

Рис. 16.7. Синтез расписания движения поездов

Мы имеем дело с трудно формализуемой задачей и с необходимостью расширения интеллектуальных возможностей диспетчера. Конструируя нейросеть, мы должны выделить основные события, характеризующие исходную ситуацию. Относительно этих событий у нас должен быть ясный ответ вида "да – нет", "1 – 0".

Как бы мы могли автоматизировать решение этой задачи (к сожалению – для каждого конкретного перегоа), на основе богатого опыта диспетчера-эксперта?

Во-первых, мы должны определить понятие "ситуация", выделив и систематизировав все ее показатели и характеристики: максимальное количество поездов, следующих через перегон в разных направлениях, и допустимые интервалы следования, типы поездов, различные сочетания этих типов, установленные скорости движения и допустимые отклонения, разрешенные остановки, длину состава (при известной длине резервных путей на пунктах перегона). Мы должны научиться задавать входные ситуации на входном слое нейросети.

Во-вторых, мы должны выделить эталонные ситуации и, подобно эксперту, сопоставить им картинки, похожие на представленную на рисунке. То есть за каждой картинкой мы должны закрепить нейрон выходного слоя сети и проложить трассу – опорный путь возбуждения от каждого эталона к соответствующей картинке.

Нейросеть позволит нам уйти от статики экспертной системы (фактически, таблицы) к динамике, позволяющей по любой случайной ситуации получать ответ на вопрос: "какая картинка в большей степени следует этой ситуации?"

Однако такой простой ответ не может исключить аварии. Т.е. на этом анализ ситуации закончить нельзя. Мы не использовали пока всю информацию, которую нам сообщила нейросеть.

Какую же информацию нам следует использовать?

Во-первых, сравнение величины возбуждения нейрона выходного слоя (хотя и максимальной) по предъявленной ситуации с величиной возбуждения этого нейрона по эталону может свидетельствовать о степени доверия полученному ответу. Если эта разница лежит в пределах экспериментально установленной точности, то считаем, что ответ найден. Если же мы считаем, что точность недостаточна, мы можем построить (автоматически, конечно) приоритетный ряд, выделив нейроны выходного слоя с близкими (ближайшими) величинами возбуждения. Эти величины возбуждения нейронов образуют веса, с которыми должны быть учтены соответствующие этим нейронам картинки.

Во-вторых, должна быть решена проблема формирования "средней" картинки по нескольким картинкам с их весами, где основные элементы картинок должны сместиться в некоторое среднее положение. Только тщательное экспериментальное исследование может ответить на вопрос о возможности и конкретной практической применимости такого решения проблемы.

Например, на обозреваемом отрезке времени поезд появляется на контролируемом перегоне. Вопросы:

1. Сколько поездов на обслуживании

   • n = 1?
   • n = 2?
   • .........
   • n = n_max?

2. Момент появления поезда

   • t = 1?
   • t = 2?
   • .........
   • t = t_max?

3. Направление движения

   • от пункта А?
   • от пункта В?

4. Тип поезда

   • скорый?
   • товарный? и т.д.

Так – по всем поездам на отрезке времени планирования. Таким образом, на основе обстановки, которая ожидается на период планирования, необходимо составить сложную "картинку" – график движения.

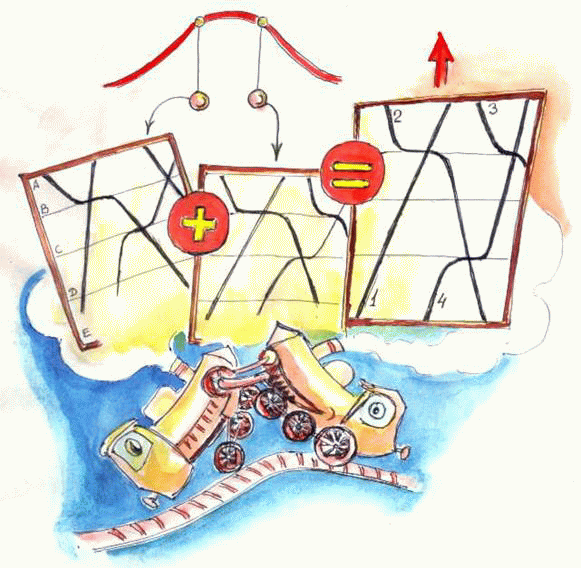
Однако мы говорим об ассоциативном мышлении, реализуемом нейросетью, о возможности нейросети интерполировать принимаемое решение. Что означает такой ответ нейросети: "На 60 из 100 это – "картинка" А, но на 30 из 100 это – "картинка" В, а на 8 из 100 это – "картинка" С"?

Такой ответ наводит на мысль о возможности автоматического выполнения операций над "картинками". Но возможность операции (в данном случае – получение "средней картинки") должна быть строго обоснована непрерывностью основных параметров, отсутствием скачков. Например, кажущаяся непринципиальной разница в один вагон может привести к тому, что на станции Пырловка поезд не впишется в длину запасного пути.

"Средняя картинка" может быть получена на основе, например, зависимости

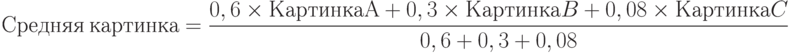
где "+" – условная операция наложения "картинок", "x" – применяется с весом данной "картинки" и определяет долю ее участия в формировании "картинки"-результата.

Графически это может означать направление смещения, растяжения и сжатия, в общем – деформации основных общих элементов "картинок" А, В, С для получения результата.

Кстати, на основе такой операции преобразования картинок можно получать среднестатистические образы населения стран и регионов, этническое прогнозирование и другие интересные вещи.

В любом случае работа нейросетевого диспетчера должна сопровождаться работой анимационной модели, красочно имитирующей движение поездов по сформированному графику и эффектно, в деталях воспроизводящей возможную катастрофу. Это может служить самостоятельным предметом развлечений диспетчера (гражданина) на его трудовом посту. В серьезном же применении такая модель может служить средством обучения нейросети.

А потому всегда должно быть предусмотрено окончательное принятие решения человеком!