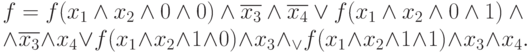|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Математическая логика событий
1.1 Булева концепция алгебры высказываний о событиях
" Ученые объяснения большей частью производят то впечатление, что бывшее ясно и понятно становится темно и запутанно".
Определение 1. Предполагаемое или свершившееся действие, его фигурант, результат, а также условия свершения, называются событием .
Определение 2. Событие выражается высказыванием о его свершении.
Высказыванию о событии (далее - просто высказывание, считая событие и высказывание о нем синонимами) можно поставить в соответствие переменную, которая в рамках булевой концепции может принимать значение ИСТИНА (1) или ЛОЖЬ (0).
Например:
x = <поезд опоздал на пять минут>;
y = <в данной операции принимал участие Вася>
(достаточно сообщить лишь имя);
z = <скорость автомобиля принадлежит диапазону (120-140 км/ч)>
(достаточно кратко обозначить диапазон в известном контексте,
как условие свершения некоторого действия,
приведшего к автокатастрофе).Очевидно, что каждая переменная x, y, z может принимать одно из двух значений - 0 или 1.
Над высказываниями производятся логические операции.
В рамках последующих построений потребуются четыре операции: отрицание ( 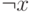 , НЕx, x ), конъюнкция (
, НЕx, x ), конъюнкция ( 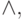 И, AND, x ),
дизъюнкция (
И, AND, x ),
дизъюнкция ( 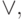 ИЛИ, OR ), импликация или операция следования (
ИЛИ, OR ), импликация или операция следования ( 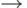 ).
Результаты операций определяются таблично.
).
Результаты операций определяются таблично.
Предполагая достаточные знания слушателей, можно напомнить:
- одноместная операция отрицания меняет значение переменной на противоположное;
- двуместная операция конъюнкции над двумя и (рекурсивно) более переменными порождает значение 1 тогда и только тогда, когда все переменные имеют значение 1;
- двуместная операция дизъюнкции над двумя и (рекурсивно) более переменными порождает значение 1, когда хотя бы одна переменная имеет значение 1;
- переменная справа от знака операции следования (импликации) принимает значение 1 тогда и только тогда, когда выражение слева от этого знака имеет значение 1.
Кроме того, ниже используется операция ИСКЛЮЧАЮЩЕЕ ИЛИ, предполагающая возможность лишь единственного вхождения переменной со значением 1 в операцию дизъюнкции, объединяющую несколько переменных.
Переход от высказываний к их булевой интерпретации, к булевым переменным, вводит в действие все законы, свойства и правила эквивалентных преобразований, известные из булевой алгебры.
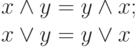 |
( 1.1) |
 |
( 1.2) |
 |
( 1.3) |
 |
( 1.4) |
Закон идемпотенции:
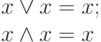 |
( 1.5) |
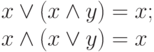 |
( 1.6) |
Закон склеивания:
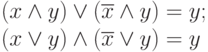 |
( 1.7) |
Операция переменной с инверсией:
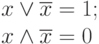 |
( 1.8) |
Операция с константами:
 |
( 1.9) |
Двойное отрицание:
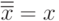 |
( 1.10) |
Несмотря на наличие дистрибутивных операций, существует ранжирование операций - в сторону понижения
(ранга) слева направо: 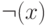 ,
, 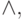
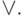 То есть если написано
без скобок
То есть если написано
без скобок 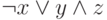 , то с помощью эквивалентного обозначения и скобок можно выявить следующий
порядок действий:
, то с помощью эквивалентного обозначения и скобок можно выявить следующий
порядок действий: 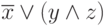 .
.
1.2. Логические функции высказываний
Множество логических переменных - высказываний о событиях {x1, x2, ..., xn} в контексте некоторого приложения образует пространство событий размерности n. Точка этого пространства является ситуацией.
Можно записать произвольную композицию на основе заданного множества переменных-высказываний
и логических операций, например,  ,
,  .
Почему первую композицию следует считать бессмысленной? По-видимому, потому, что она содержит конструкции,
не определенные в терминах алгебры логики, и не может быть исчерпывающим образом преобразована в таковые на
основе применения (1)-(10).
Тогда вторая приведенная композиция имеет смысл, т.к. полностью подвержена основным определениям операций
алгебры логики и правилам преобразования в ней.
.
Почему первую композицию следует считать бессмысленной? По-видимому, потому, что она содержит конструкции,
не определенные в терминах алгебры логики, и не может быть исчерпывающим образом преобразована в таковые на
основе применения (1)-(10).
Тогда вторая приведенная композиция имеет смысл, т.к. полностью подвержена основным определениям операций
алгебры логики и правилам преобразования в ней.
Высказывания (о событиях ) в качестве переменных могут входить в состав сложных формирований - логических функций, принимающих (булевы) значения 1 (ИСТИНА) или 0 (ЛОЖЬ).
Определение 3. Имеющая смысл линейно-скобочная композиция операций 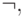
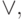
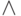 над переменными-высказываниями x1,
x2, ..., xn, образующими пространство событий, задает логическую функцию f(x1,
x2, ..., xn), принимающую для различных ситуаций, т.е. наборов значений переменных, значения 0 или
1.
над переменными-высказываниями x1,
x2, ..., xn, образующими пространство событий, задает логическую функцию f(x1,
x2, ..., xn), принимающую для различных ситуаций, т.е. наборов значений переменных, значения 0 или
1.
Таким образом, логическая функция является булевой функцией ситуаций.
В классической теории булевых функций [1] показывается, что каждая такая функция может быть представлена дизъюнктивной и (или) конъюнктивной нормальной формой. В первом случае ее структура выражается как дизъюнкция конъюнкций, во втором - как конъюнкция дизъюнкций.
Рассмотрим две логические функции
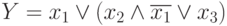 и
и
 .
.
Выражение Y представлено дизъюнктивной нормальной формой ( ДНФ ). Выражение Z соответствует конъюнктивной нормальной форме (КНФ), практически не применяемой.
Преобразуем
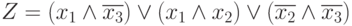 .
(Учитывается, что
.
(Учитывается, что 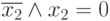 .)
.)
Это - дизъюнктивная нормальная форма.
Практически, например, при конструировании электронных устройств, известно наперед, какой сигнал на отдельно взятом выходе должен формироваться при различных значениях сигналов на входе. Тогда значения логической функции, описывающей формирование сигнала на данном выходе, задаются таблично, в зависимости от всех возможных ситуаций на входе. По такой таблице аналитическое выражение для искомой логической функции формируется в виде совершенной дизъюнктивной нормальной формы (СДНФ). Ее общий вид продемонстрируем на примере трех переменных:
 |
( 1.11) |
Для всех значений переменных рассчитаем значения приведенных выше логических функций Y и Z (табл. 1.1).
| x1 | x2 | x3 | Y | Z |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Попытаемся построить приведенные выше функции Y и Z на основе их СДНФ, т.е. проверим правильность такого подхода:

После эквивалентных преобразований (начинающихся с вынесения x1 "за скобку") получим
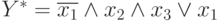 , что совпадает с видом Y.
, что совпадает с видом Y.
Аналогично,

После эквивалентных преобразований находим

Из табл. 1.1 видно, что все значения Z и Z*
от одних и тех же наборов значений переменных совпадают. Однако Z*
образуется только двумя "слагаемыми" Z. Конъюнкция 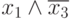 оказалась "лишней", не влияющей на результат. Это говорит о том, что формирование аналитического вида логической функции по ее табличному заданию, с помощью СДНФ,
позволяет получить простейшее (лаконичное) представление, без лишних конструкций, не влияющих на результаты вычислений.
оказалась "лишней", не влияющей на результат. Это говорит о том, что формирование аналитического вида логической функции по ее табличному заданию, с помощью СДНФ,
позволяет получить простейшее (лаконичное) представление, без лишних конструкций, не влияющих на результаты вычислений.
В заключение этого раздела представим обобщение, построенное над СДНФ, - в соответствии с теоремой разложения, широко используемой при конструировании электронных схем на основе стандартного набора элементов. Как и ранее, продемонстрируем суть данной теоремы на примере четырех переменных: