|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Основы "живого" моделирования
"Мы, собаки, в смысле нервной восприимчивости в семь и еще много раз тоньше людей… Я чувствую тайными, неведомыми, дрожащими путями, как их души краснеют, бледнеют, трепещут, завидуют, любят, ненавидят".
15.1. Какую задачу мы хотим решить?
Рассмотрим принципы построения управляемых видимых объектов в трехмерной памяти компьютера. Для имитации их движения используем "мышцы" и шарниры. Мышцы воспринимают команды на сокращение. Предложим эмпирические формулы для переноса содержимого ячеек памяти при имитации движения. Движение может задаваться программно. Однако подсоединение объектов к логической нейросети открывает большие возможности непредсказуемости реакции объектов на внешние факторы. Это, в свою очередь, открывает перспективу применения реагирующих объектов в сфере игр, развлечений, сценических постановок, в интеллектуальных системах отображения и в других видах искусства и бизнеса.
Во всех предыдущих лекциях в качестве примеров возможного применения обсуждается построение систем с элементами искусственного интеллекта, которые можно отнести к области искусства и развлечений. Фантазия легко связывает создание монстров, объектов компьютерных игр, имитацию их реакции на внешнюю среду или другие предлагаемые им объекты и ситуации с такими "мероприятиями", как парк фантасмагорий, Disneyland, цирк марионеток, распознавание "свой — чужой", сетевые зрелищно-рекламные демонстрации и т.д. Такие системы могут представлять как искусство, так и бизнес.
Существуют два направления реализации указанных систем ИИ: натурное и компьютерное.
В современном парке (культуры и отдыха) можно в натуральном виде встретить не одно существо, мало отличающееся от живого и совершающее действия и движения по заложенной программе. Технологии их построения можно считать отработанными, имитация движений, включая работу "мышечного" аппарата, вполне совершенна. Отсутствие элементов ИИ, предполагающих непредсказуемость реакции, — основной недостаток таких объектов.
Компьютерная реализация сегодня ограничена мультимедийными средствами двумерной и трехмерной графики. Возможности создаваемых этими средствами систем и образов огромны. Достаточно отметить такое средство, как 3D-MAX, позволяющее создавать целые кинофильмы. Однако основной недостаток всех известных систем кроется в априорном знании возможных сцен, сглаживание перехода через которые в реальном времени имитирует движение. Это подобно табличному заданию огромного количества значений функции многих переменных при игнорировании непосредственного расчета.
Непредсказуемость сцен, возникающая при имитации реакции моделируемого объекта на внешние воздействия, может потребовать огромного, практически нереализуемого числа предполагаемых возможных сцен.
В этом случае желательно при построении объекта (монстра, человека и др.) снабжать его управляемыми органами движения (модификации, деформации, имитирующей улыбку, движение руки и т.д.), подобными мышцам. Их необходимо соединить с управляющим элементом — жестко заданной программой. Однако такая программа может предполагать анализ ситуации или внешних воздействий. Это уже напрямую требует применения аппарата логических нейронных сетей, одновременно и в разной степени реализующих ряд отношений вида "если …, то …", что наиболее близко к поведению живого существа.
Таким образом, построение реального объекта в памяти компьютера, а не его математического образа, задание ряда рычагов — "мышц", которые способны деформировать или видоизменять объект в соответствии с формируемыми извне командами, использующими коэффициент сжатия, позволяют имитировать любое, в том числе непредсказуемое, движение объекта. (Ниже будет отмечена необходимость механизмов перемещения и вращения.)
Становятся видными новые возможности для создания кинофильмов, сценических постановок и других видеосценариев.
Построение реальных объектов требует имитации объемной, трехмерной памяти и введения основных процедур ее преобразования.
Заметим, что проблемы компьютерной реализации "живого" моделирования целиком включают в себя проблемы натурного моделирования, оставляя второму лишь проблемы химического, технологического и электротехнического (возврат к релейно-контактным схемам?) свойства, что, как сказано выше, сейчас успешно решается.
15.2. Моделирование трехмерной памяти
Поскольку компьютер, реализующий "живую" модель, несомненно, должен обладать рядом свойств, обнаруживаемых в процессе дальнейшего изложения, справедливо назвать его видеонейрокомпьютером (ВНК). Это тем более справедливо, что обработка большого числа ячеек памяти предъявляет те же требования к распараллеливанию, что и обработка большого числа нейронов сети.
Отметим, что современные персональные компьютеры (РС) и рабочие станции, реализующие системы мультимедиа, вполне способны выполнять функции такого нейрокомпьютера. Однако потребность интеграции памяти нескольких компьютеров может потребовать применения локальной вычислительной сети, удовлетворяющей требованиям работы в реальном времени. И уж без сомнения, параллельная вычислительная система SPMD-архитектуры [9] c большой оперативной памятью в наибольшей степени адекватна рассматриваемой задаче.
Назовем ячейку, занятую элементом объекта, клеткой этого объекта. Как видно далее, клетка минимально должна содержать информацию о цвете (пиксель), коэффициенте освещенности, указателе вершины стека.
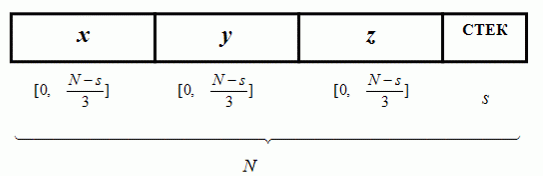
Пусть адресное пространство ВНК при сквозной линейной адресации ячеек определяется N разрядами. Адрес разбивается на четыре части (рис. 15.1).
Здесь x, y, z — координаты клетки в трехмерной памяти ; s разрядов отводятся для адресации стека, сопровождающего каждую клетку. Стек необходим для сохранения информации в случае сжатия объекта — для более точного его восстановления. Таким образом, адресное пространство хранения клеток объекта или целой сцены составляет 2N-s , что говорит о необходимом весьма большом значении N. Значение s практически может быть не более трех.
Трехмерная память — это перспективная разработка. Она предполагает непосредственный (невиртуальный) доступ пользователя на этапе программирования как к памяти, так и к адресам данных при указанной структуре адреса.
При моделировании трехмерная память в виртуальной памяти современного компьютера задается трехмерным массивом S[0:P; 0:P; 0:P] переменных S[i, j, k], где значения индексов являются координатами соответственно x, y, z. Тогда задача деформации или перемещения объектов преобразуется в задачу нахождения новых значений этих индексов для каждой переменной, являющейся клеткой объекта — для выполнения соответствующего переноса.
При этом линейный адрес переноса или текущего нахождения клетки объекта находится так:
<S[i, j, k]> = C + i + jP + kP2.
Здесь С — базовый адрес массива.
Стек моделировать нецелесообразно. Информация, потерянная при сжатии объекта, может быть восстановлена с помощью интерполяции.
15.3. "Мышца" и ее сокращение
Пусть объект в трехмерном пространстве задан своей оболочкой. Каждый элемент оболочки является клеткой. Оболочка формируется при создании объекта. В общем случае объект может быть заполнен значащей информацией и внутри, если его вид в разрезе интересует пользователя.
"Мышца" (далее кавычки опустим) как рычаг управления деформацией объекта задается пользователем-разработчиком в центральной системе координат координатами начала и конца, а также точкой неподвижности, относительно которой возможно сокращение мышцы. Точка неподвижности может совпадать с началом или концом мышцы. (Конечно указанные точки обозначаются мышью; координаты при этом выставляются автоматически.) По умолчанию точка неподвижности является серединой мышцы. Мышца не обязательно связывает точки оболочки. В общем случае она может располагаться внутри и даже вне объекта, принадлежа ему и влияя на его деформацию.
Мышцы объекта являются невидимыми, входящими в список мышц данного объекта и допускающими реакцию на приказы извне.
Таким образом, мышца (рис. 15.2) — это невидимый отрезок АВ, связывающий точки A(x1, y1, z1) и B(x2, y2, z2) , отображающий некоторое геометрическое место клеток объекта. Этот отрезок связан с объектом и может сокращаться при подаче управляющих импульсов и восстанавливаться при их отсутствии. Такое изменение отрезка производится относительно некоторой принадлежащей ему точки М(xM, yM, zM) . Сокращение мышцы сопровождается пространственным переносом (уплотнением) клеток объекта, которые принадлежат (с точностью до дискретности адресации) отрезку, обозначающему эту мышцу.
Параметрическая система уравнений, описывающих отрезок АВ, имеет вид
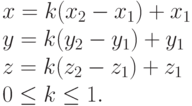 |
( 15.1) |
Напоминаем, что координаты точек объекта совпадают с адресами памяти, по которым находятся соответствующие клетки, так что систему уравнений (15.1) с точностью до целочисленной дискретности адресации можно рассматривать относительно трехмерных адресов . Это и подразумевается в дальнейших выкладках.
Пусть l — коэффициент сжатия мышцы. Тогда отрезок АМ необходимо преобразовать в отрезок А*М с длиной lx|А*М|, а отрезок МВ — в отрезок МВ* с длиной lx |МВ*|.
Рассматривая по каждой координате отдельно, убеждаемся, что отрезок x1xM необходимо преобразовать в отрезок x1* xM с длиной l(xM- x1) , отрезок xMx2 необходимо преобразовать в отрезок xMx2* c длиной l(x2 - xM) . Аналогично отрезок y1yM должен быть преобразован в отрезок y1* yM с длиной l(yM - y1) и т.д.
Это, в частности, означает, что клетка с координатой x1 должна быть переслана в ячейку, определяемую соответствующей составляющей адреса l(xM - x1) и т.д.