|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Трассировка нейронной сети
" - Аннушка
Аннушка?.. - забормотал поэт, тревожно озираясь, - позвольте, позвольте
К слову "Аннушка" привязались слова "подсолнечное масло", а затем почему-то "Понтий Пилат". Пилата поэт отринул и стал вязать цепочку, начиная со слова "Аннушка". И цепочка эта связалась очень быстро и тотчас привела к сумасшедшему профессору".
4.1. Пример - опыт - предпосылки обобщения
Объединим множество эталонов, требующих возбуждения одного нейрона выходного слоя, понятием "обобщенный эталон". Например, эталоны  ,
,  ,
,  ,
,  ,
,  образуют один обобщенный эталон
образуют один обобщенный эталон 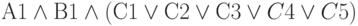 ,
ведущий к R1. Тогда для обобщенного эталона введем понятие обобщенной операции &, которая объединяет все посылки, ведущие к одному выводу, A1&B1&C1&C2&C3&C4&C5->R1.
,
ведущий к R1. Тогда для обобщенного эталона введем понятие обобщенной операции &, которая объединяет все посылки, ведущие к одному выводу, A1&B1&C1&C2&C3&C4&C5->R1.
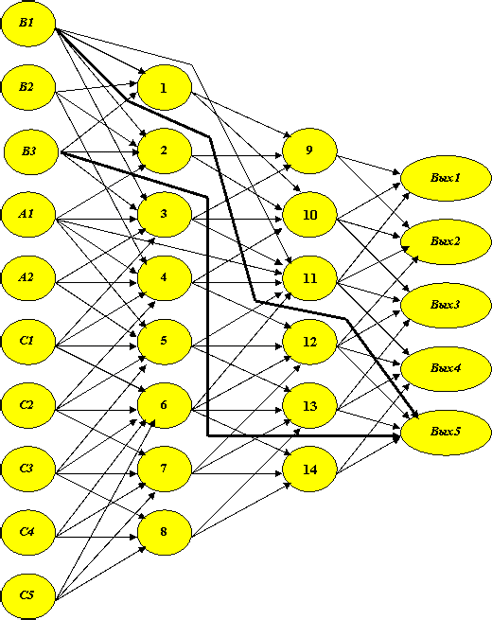
Выберем нейросеть, отражающую, как нам кажется, все особенности, которые необходимо учесть при построении алгоритма трассировки, и, как мы уже начали, возьмем тот же пример, который выглядит теперь следующим образом:
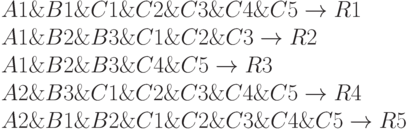 |
( 4.1) |
Мы хотим, задавая обобщенный эталон на входе, например из тех, что приведены выше, экономным путем построить, возможно, пересекающиеся пути возбуждения, ведущие от каждого возбужденного входного нейрона в соответствующий нейрон выходного слоя. Способ должен быть экономным в том смысле, что пути должны быть максимально объединены, совмещены, реализуя стратегию слияния и выхода на общую, единую дорогу, ведущую к заветной цели.
При этом мы строим эвристический алгоритм, который крайне экономно расходует ресурсы сети - ее нейроны и связи, но и так же экономно вводит изменения, развивает сеть, если связей оказывается недостаточно.
Ибо мы видели, с каким трудом удается приспособить "готовую" нейросеть под конкретную задачу. Мы постоянно склонялись к вопросу: "А не лучше ли сразу строить сеть "под задачу", а не наоборот?" Нам кажется, мы нашли диалектический компромисс: беря что-то близкое, подходящее, мы минимально переделываем, словно костюм с жмущим гульфиком, купленный в универсальном магазине. Кроме того, нам очень важно сделать алгоритм доступным широким массам студенческой молодежи, овладевшей основами таинства параллельного программирования!
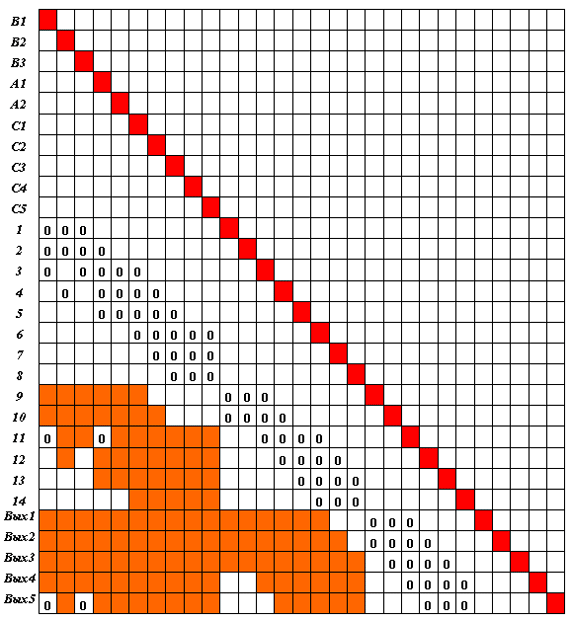
Пусть выбранная нейросеть представлена на рис. 4.1, где первоначально заданные связи обозначены тонкими стрелками. Строим соответствующую матрицу следования S и в ней - транзитивные связи (рис. 4.2). Проверяем, все ли нейроны выходного слоя достижимы из любого нейрона входного слоя. Если нет, считаем, что сеть составлена не корректно.
В данном случае из нейрона В1 не исходит ни одной статической цепочки, заканчивающейся нейроном Вых5. Это следует из того, что в строке, соответствующей нейрону Вых5, нет даже транзитивной связи в столбце, соответствующем нейрону В1. То же касается нейрона В3.
Введем синапсические связи В1 -> Вых5 и В3 -> Вых5, что отмечено на рис. 4.1 жирными стрелками, а на рис. 4.2 – нулевыми весами введенных связей.
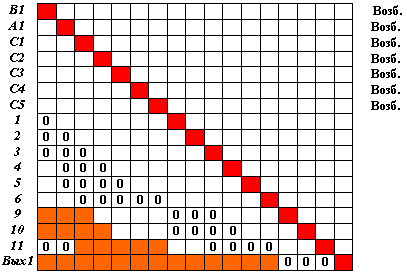
Сформируем статический путь возбуждения {B1, A1, C1, C2, C3, C4, C5} -> Вых1 и отобразим его матрицей S1[B1,A1,C1,C2,C3,C4,C5 -> Вых1] на рис. 4.3.
Пытаясь сымитировать прокладываемые пути возбуждений, снабдим все нейроны входного слоя, отраженные в этой матрице, признаком "возбужден".