|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
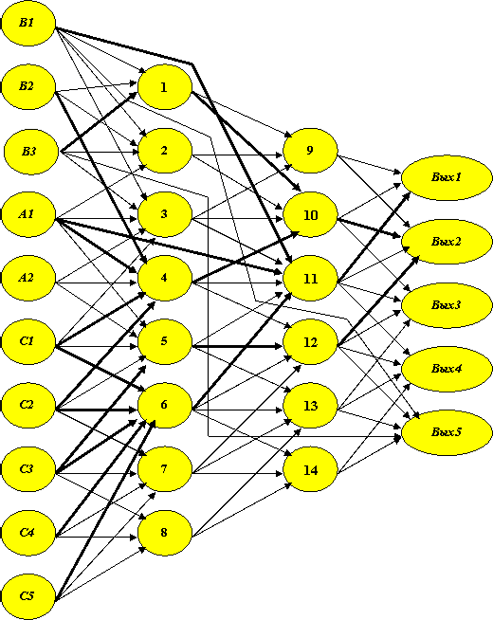
Трассировка нейронной сети
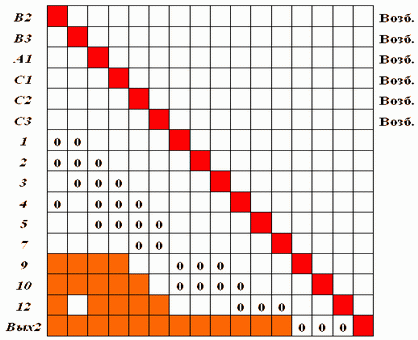
Исключим из данной матрицы строки и столбцы, соответствующие нейронам 6 и 11. Матрица примет вид, показанный на рис. 4.9.
Объединяем столбцы множества входов матрицы, обладающих признаком "возбужден". На данном шаге - это первые шесть столбцов матрицы. Находим в них первую строку, содержащую максимальное число нулей. Это строка, соответствующая нейрону 4. Меняем в ней все нули на единицы, полагаем m4 = 4. Присваиваем нейрону 4 признак "возбужден". Отражаем внесенные изменения весов в матрице S.
Исключаем из матрицы S2 строки и столбцы, соответствующие нейронам В2, А1, С1, С2, "передавшим" свое возбуждение нейрону 4.
Вновь объединяем столбцы множества входов, обладающих признаком "возбужден". Это столбцы, соответствующие нейронам В3, С3, 4. В совокупности этих столбцов выбираем первую из строк, содержащую максимальное число нулей. В данном случае это строка, соответствующая нейрону 1. Меняем нуль на единицу, полагаем m1 = 1, нейрону 1 присваиваем признак "возбужден".
Исключаем из матрицы строку и столбец, соответствующие нейрону В3, "передавшему" возбуждение нейрону 1. Исключаем из матрицы строки и столбцы, соответствующие образовавшимся входам - "не возбужденным" нейронам 2 и 3.
Выделяем столбцы, которые соответствуют нейронам - входам, обладающим признаком "возбужден", и в их совокупности находим строку, обладающую наибольшим числом нулей. Такая строка соответствует нейрону 10. Меняем нули на единицы, присваиваем нейрону признак "возбужден", полагаем m10 = 2.
Исключаем из матрицы S2 строки и столбцы, которые соответствуют нейронам 1 и 4, передавшим возбуждение нейрону 10.
Нейрон 9, не обладающий признаком "возбужден", образует вход матрицы. Исключаем соответствующие ему строку и столбец.
Выделяем столбцы, соответствующие нейронам С3 и 10, и в них находим строку с максимальным числом нулей. Первая из таких строк соответствует нейрону 5. Заменяем в ней единственный нуль единицей, присваиваем нейрону признак "возбужден", полагаем m5 = 1. Отражаем изменение веса в матрице S.
Исключаем из матрицы S2 строку и столбец, которые соответствуют нейрону С3, передавшему возбуждение нейрону 5.
Исключаем строку и столбец, соответствующие нейрону 7, как порождающему вход матрицы и не имеющему признака "возбужден".
В совокупности выделенных столбцов, соответствующих нейронам 5 и 10, строка, соответствующая нейрону 12, имеет единственный нуль. Меняем его на единицу, присваиваем нейрону 12 признак "возбужден", полагаем m12 = 1. Отражаем внесенное изменение веса в матрице S. Исключаем из матрицы S1 строку и столбец, соответствующие нейрону 5.
И, наконец, на последнем шаге, заменяя нули в строке, соответствующей нейрону Вых2, единицами, мы получим окончательный искомый путь возбуждения. Отразим его на рис. 4.10 нейросети.
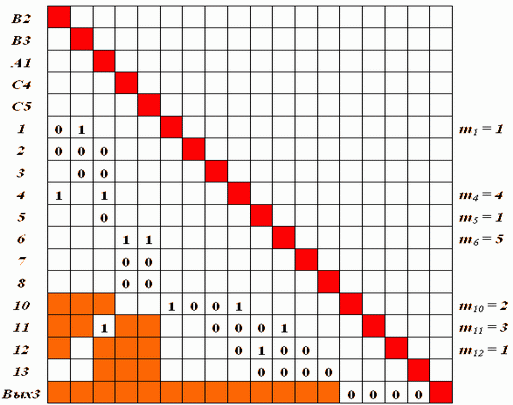
Обучим сеть третьей ситуации, требующей решения R3. Закрепим за этим решением нейрон Вых3. Матрица S3[B2, B3, A1, C4, C5 -> Вых3] представлена на рис. 4.11.
Исключаем из матрицы S3 представительство тех ранее использованных ("возбужденных") нейронов, для которых значение m (указано в дополнительном столбце матрицы) превышает количество единиц в соответствующей строке. Это значит, что эти нейроны "собрали" уже возбуждение нейронов, которые в данном пути возбуждения, т.е. в матрице S3, не используются. Это нейроны 4, 5, 6, 11. Переиспользование их невозможно.
Повторяем попытки исключения из матрицы S3 представительства тех нейронов, для которых значение m стало превышать количество единиц в соответствующей строке. И так далее - до исчерпания этой возможности.
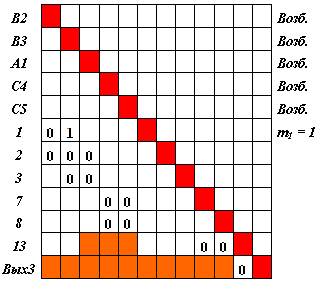
В данном случае нам придется исключить из рассмотрения (вследствие исключения нейронов 4 и 5 ) нейроны 10 и 12. Матрица S3 примет окончательный вид на рис. 4.12.