Построение современной нейросетевой технологии

3.6. Модель механизма запоминания

Главный механизм запоминания, реализованный в природе, можно представить так. Импульс возбуждения, проходя через синапс, "нагревает" и уменьшает его сопротивление, увеличивая синапсический вес. В последующих тактах, при последующих предъявлениях эталона, импульс возбуждения увереннее одолевает путь возбуждения, с большей определенностью указывая соответствующий образ (как говорится, "Сложилась связь"), а используемые при этом синапсы, "подогреваясь", сохраняют и, возможно, увеличивают вес.

Здесь работает известное правило Хебба [19, 20]: Синапсический вес связи двух возбужденных нейронов увеличивается.

Таким способом даже достигается эффект локализации и максимизации возбуждения на выходном слое, дублирующий, а возможно, исключающий необходимость взаимодействия соседних нейронов.

По-видимому, синапсы обладают свойством "остывания" со временем, если нет подтверждения их использования. Такое предположение адекватно свойству нашей памяти: ненужная, не подтверждаемая и не используемая периодически информация стирается ("Связи рвутся!"). Стирается до такой степени, что приходится учиться заново.

Отметим и важную роль воображения: эталоны на входном слое поддерживаются достаточно долго, возобновляются или моделируются. По-видимому, здесь большое значение имеет эпифиз, "третий глаз" - орган воображения и медитации, память и генератор видений.

При создании искусственных механизмов обучения нейросети возникают вопросы:

• Увеличивать ли веса всем нейронам, образующим статический путь возбуждения - для запоминания эталона?
• Увеличивать ли веса только вдоль некоторых (опорных) цепочек статического пути возбуждения?
• Увеличивать ли веса только нейронов, образующих динамический путь возбуждений ; ведь выше предполагалось, что уже само возбуждение увеличивает вес связи? Зачем возбуждать дополнительные нейроны, если и этих достаточно?

По-видимому, третий аспект в большей степени соответствует самообучению, самонастройке. Вмешательство в наш мозг на этом уровне исключено. Однако система искусственного интеллекта - в более выгодном положении. Ведь она находится под нашим неусыпным контролем, реализуя обучение "с учителем", и допускает любое вторжение, корректирующее вынужденные недостатки естественного интеллекта. Поэтому, рассматривая пример (и пытаясь накопить хоть какой-то опыт), мы будем увеличивать веса синапсических связей нейронов, составляющих выделенные цепочки статического пути возбуждения от эталона к образу. Назовем такой метод методом опорных путей, который выработан в процессе проведения многочисленных экспериментов. В частности, увеличение синапсических весов большого числа нейронов приводило к неудачам, связанным с корреляцией динамических цепочек возбуждения для разных эталонов и с быстрым насыщением нейросети (недостаток многих известных алгоритмов обучения). В процессе обучения многим эталонам рано или поздно все веса сети оказывались повышенными, и она прекращала что-либо различать. Начиналась путаница согласно выражению "Ум за разум заходит!"

Что же касается величины изменения синапсических весов, то вряд ли необходимо относительно каждого нейрона решать системы дифференциальных уравнений в частных производных. (Речь идет о методе обратного распространения ошибки, подробно изложенном в [20].) Природа больше рассчитывает на авось, "на глазок" и другие мудрые и практические приблизительные ориентиры, малопривлекательные теоретически. В данном случае нас более обнадеживает "прилив крови" в нужном направлении, стимулируемый информационным раздражителем или легким подзатыльником. В связи с этим введем некую переменную , выверяемую практически (а то и просто единицу), уменьшаемую или увеличиваемую при необходимости.

Таким образом, нам удалось перейти от схемотехники к нейротехнологии, от точного, определенного к приблизительному, неопределенному. Действительно, не могла эволюция, основанная на принципе "делай все, что можно", методом "проб и ошибок" привести к производству точных электронных схем, упрятанных в черепную коробку. Да и нет в природе точной, абсолютно достоверной информации. Но общие логические принципы и зависимости должны быть воплощены и в той и в другой технологии.

3.7. Применение "готовых" нейросетей

Справедливо желание построения универсальных моделей нейросетей в составе программного обеспечения компьютера, снабженных механизмами приспособления под задачу пользователя. Еще более справедливо желание построить набор аппаратных средств - нейросетей (нейрокомпьютеров, НК), сопряженных с компьютером и, по выбору пользователя, участвующих в решении сложных задач. Такие аппаратно реализованные нейросети, как приставки или внешние устройства компьютера, например, определяют специальное направление использования ПЛИС - интегральных схем с программируемой логикой.

3.7.1. Однослойная нейросеть

Для наглядности воспользуемся как матричным, удобным алгоритмически, так и графическим представлением нейросети.

Однослойная нейросеть, составленная по принципу "каждый с каждым", представлена на рис. 3.11.

Рис. 3.11. Формирование однослойной нейросети

Пусть используется предложенная выше передаточная функция

Значения 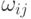предстоит подобрать, а значения h_i положим равными нулю.

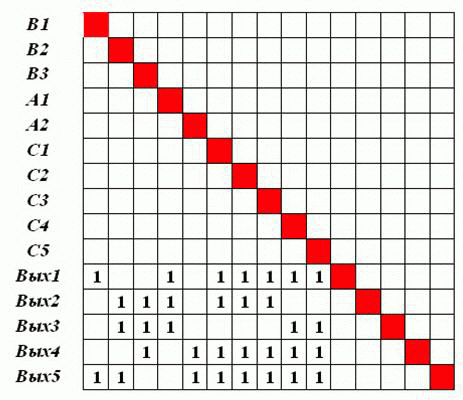
Закрепим 10 нейронов входного слоя за исходными данными, 5 выходов - за решениями. Этим мы выделим интересующую нас подсеть, которой соответствует матрица следования на рис. 3.12.

Рис. 3.12. Матрица следования для однослойной нейросети

Здесь отображен ее окончательный вид, т.к. сначала все веса связей принимаются равными нулю.

Для того чтобы сформировать решение R1 на нейроне Вых1, надо значительно увеличить веса связей этого нейрона с нейронами В1, А1, С1, С2, С3, С4, С5, т.е. построить статический путь возбуждения [B1, A1, C1, C2, C3, C4, C5] -> Вых1 и вдоль него по некоторой дисциплине увеличить веса связей.

В данном случае результат очевиден, поэтому обратим внимание на некоторый общий подход.

Установим веса связей между нейронами В1, А1, С1, С2, С3, С4, С5 с одной стороны, и нейроном Вых1 - с другой равными единице, оставив нулевыми веса связей этого нейрона с другими нейронами входного слоя. Таким образом полностью исключается влияние других нейронов входного слоя на данный выходной нейрон. Конкретная задача может потребовать корректировки, учета взаимного влияния всех входных ситуаций в результате тщательного экспериментального исследования задачи.

Здесь вновь прослеживается преимущество нейросети, способной элементарно просто учитывать наблюдаемые или интуитивно предполагаемые поправки, требующие огромных исследований и расчетов.

Поступив так же со всеми выделенными нейронами выходного слоя, получим окончательный вид матрицы следования (рис. 3.12). Построенная нейросеть полностью соответствует специальной сети "под задачу", представленной на рис. 3.7.

…Так какую же сеть предложить дяде Рамзаю? Ведь надо и подоходчивее, и попрактичнее, но и так, чтобы не казалось уж слишком просто.