|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Построение современной нейросетевой технологии
3.5. Формализация нейросети
Тактирование работы сети, столь характерное для каждой управляющей системы, которая отслеживает состояние сети в дискретные моменты времени, определяет потактовое продвижение по ней волны возбуждений от входного слоя к выходному. Волна за волной, возбуждения имитируют систолическую схему вычислений - параллельный конвейер обработки отдельных кадров, соответствующих конфигурации возбуждений входного слоя в одном такте.
На практике широко исследуются многослойные сети типа персептрон, где отсутствуют обратные связи и связи возможны между нейронами только смежных слоев. В данном разделе мы также не рассматриваем обратные связи, но снимаем ограничение на "слоистость" нейросети, обеспечивая более общий подход. Именно такая нейросеть, допускающая связи "через слой", была построена в приведенном выше примере. Для таких сетей значительно упрощаются следующие построения.
Нейронную сеть можно изучать статически, исследуя ее структуру, и динамически, исследуя в ней прохождение возбуждений.
Статические исследования нейросети показывают, что она представляет собой ориентированный граф G без контуров. Вершины его соответствуют нейронам, дуги - синапсическим связям. Целесообразно такой, высший уровень представления отделить от более глубокого описания каждого нейрона и связей между ними, отображающего динамику проходящих процессов, т.е. расчет значения возбуждения нейронов в зависимости от весов синапсических связей и порогов.
Граф малопригоден для формальных исследований и компьютерных алгоритмов. Удобнее пользоваться матричным отображением нейросети. Таким способом представления можно отобразить как структуру, конфигурацию, топологию графа, так и численные значения характеристик его синапсических связей.
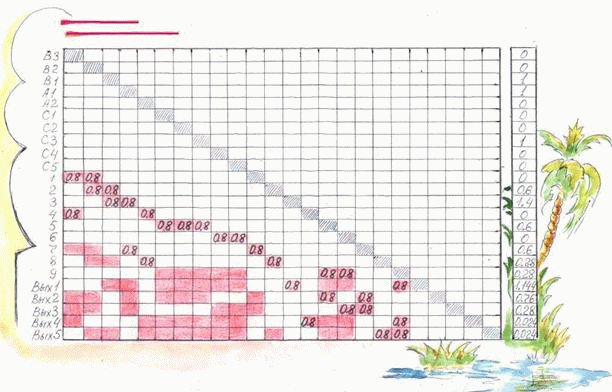
Составим матрицу следования S (рис. 3.9), число строк (и столбцов) которой равно числу нейронов сети, включая нейроны входного и выходного слоя. Каждая строка (и столбец с тем же номером) соответствуют одному нейрону.
Элемент (i, j) этой матрицы - суть непустой объект, содержащий вес 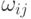 синапсической связи j -> i, если такая связь существует. В то же время элементы матрицы S
следует интерпретировать как булевы переменные, равные "1" в случае ненулевого значения указанного веса. Это разрешает
выполнение логических операций над строками и столбцами матрицы S, рассматривая ее как аналогичную матрицу следования, используемую при описании частично упорядоченных множеств работ в параллельном программировании
[6].
синапсической связи j -> i, если такая связь существует. В то же время элементы матрицы S
следует интерпретировать как булевы переменные, равные "1" в случае ненулевого значения указанного веса. Это разрешает
выполнение логических операций над строками и столбцами матрицы S, рассматривая ее как аналогичную матрицу следования, используемую при описании частично упорядоченных множеств работ в параллельном программировании
[6].
Матрицу S можно изучать в статическом режиме, исследуя и корректируя возможные пути прохождения возбуждений. По этой же матрице в динамическом режиме (моделирования) можно исследовать действительные пути прохождения возбуждений. Такое исследование связано с потактовым расчетом величин возбуждения нейронов.
Нулевые строки (входы) матрицы S соответствуют нейронам входного слоя - рецепторам, нулевые столбцы (выходы) - нейронам выходного слоя.
Нейроны образуют статические цепочки  , длины m, если существуют синапсические связи
(впредь будем опускать слово "синапсические") вида
, длины m, если существуют синапсические связи
(впредь будем опускать слово "синапсические") вида 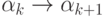 .
Составляя все статические цепочки по графу G, можно выделить одну или более цепочек максимальной длины. Такие цепочки
назовем критическими. (В традиционных многослойных моделях длина критической цепочки совпадает с числом слоев сети.)
.
Составляя все статические цепочки по графу G, можно выделить одну или более цепочек максимальной длины. Такие цепочки
назовем критическими. (В традиционных многослойных моделях длина критической цепочки совпадает с числом слоев сети.)
Пусть по статической цепочке i->j->k мы обнаружили отсутствие непосредственной связи i->k, т.е. элемент матрицы S, стоящий на пересечении k -й строки и i -го столбца, равен "0". Однако очевидно опосредствованное влияние возбуждения нейрона i на величину возбуждения нейрона k, что указывает на наличие транзитивной связи i -> k. Нахождение транзитивных связей позволяет выявлять все нейроны, потенциально возбуждающие определенный нейрон выходного слоя.
Алгоритм дополнения матрицы S транзитивными связями весьма прост.
Для всех i = 1, 2 ,..., N:
Формируем новое значение строки i логическим сложением этой строки со строками, соответствующими непустым элементам в ней. "Новые" непустые элементы заменяем на не пустые элементы, обозначающие транзитивные связи.
В нашем примере матрица S, дополненная транзитивными связями (непустые клеточки), и представлена на рис. 3.9.
Зафиксируем некоторое подмножество R нейронов входного слоя и единственный нейрон r выходного. Построим множество цепочек, ведущих из выделенного подмножества нейронов входного слоя в данный нейрон выходного слоя. Выделенное таким образом множество цепочек назовем статическим путем возбуждения данного нейрона выходного слоя по множеству нейронов входного слоя. Обозначим его R->r.
Представим алгоритм формирования статического пути возбуждения R->r.
- Вычеркиваем из матрицы следования S строки и столбцы, которые соответствуют нейронам, не принадлежащим R.
- Вычеркиваем из матрицы следования S все строки и столбцы, отображающие нейроны выходного слоя, кроме нейрона r.
- Вычеркиваем из матрицы следования S строки и столбцы, отображающие нулевые позиции строки нейрона r.
- Вычеркиваем из матрицы следования S строки и столбцы, отображающие нейроны внутренних слоев нейросети, в том случае, если в результате предыдущего вычеркивания эти строки оказались нулевыми.
- Выполняем пункт 4, пока не прекратится образование нулевых строк.
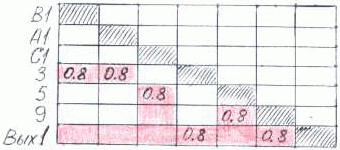
На рис. 3.10 матрицей S[B1, A1, C1 -> Вых1] отображено множество цепочек, ведущих из нейронов В1, А1, С1 в нейрон Вых1, т.е. статический путь возбуждения [B1, A1, C1] -> Вых1.
Теперь рассмотрим фактор возбуждения и проанализируем возможные динамические пути прохождения возбуждений.
Динамической цепочкой возбуждений  длины m назовем статическую цепочку, составленную из нейронов, первые m?1
которых обладают отличной от нуля величиной возбуждения.
длины m назовем статическую цепочку, составленную из нейронов, первые m?1
которых обладают отличной от нуля величиной возбуждения.
Динамическая цепочка возбуждений является вырожденной, если ее последний элемент обладает нулевой величиной возбуждения. Вырожденная динамическая цепочка возбуждений характеризует затухание сигнала.
Предъявим сети некоторый образ или эталон (не будет большой ошибки, если и здесь при предъявлении мы будем пользоваться словом "образ", ибо все есть образ чего-то), приводящий к возбуждению нейроны входного слоя, - в некоторой конфигурации. Эти нейроны образуют множество R. В результате возбуждения сети оказался возбужденным некоторый нейрон r выходного слоя. Сформировался, таким образом, динамический путь возбуждения R -> r ; очевидно, его образуют нейроны, входящие в состав статического пути возбуждения R -> r, так как некоторые нейроны могут остаться невозбужденными.
В общем случае не все нейроны, составляющие статический путь возбуждения, "работают" на возбуждение нейрона выходного слоя, поскольку возможны вырожденные динамические цепочки возбуждения, обусловленные значениями порогов передаточной функции.