Лемма Цорна и свойства операций
По лемме Цорна в нашем частично упорядоченном множестве
существует максимальный элемент. Пусть этот элемент
есть  . Мы знаем, что
. Мы знаем, что  есть
взаимно однозначное
соответствие между
есть
взаимно однозначное
соответствие между  и
и  и
потому
и
потому 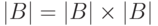 .
Теперь есть две возможности. Если
.
Теперь есть две возможности. Если  равномощно
равномощно  ,
то
,
то  равномощно
равномощно  и все
доказано. Осталось рассмотреть случай, когда
и все
доказано. Осталось рассмотреть случай, когда  не
равномощно
не
равномощно  ,
то есть имеет меньшую мощность (большей оно иметь не может,
будучи подмножеством). Пусть
,
то есть имеет меньшую мощность (большей оно иметь не может,
будучи подмножеством). Пусть  - оставшаяся часть
- оставшаяся часть  , то
есть
, то
есть  . Тогда
. Тогда 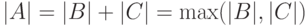 ,
следовательно,
,
следовательно,  равномощно
равномощно  и
больше
и
больше  по мощности.
Возьмем в
по мощности.
Возьмем в  часть
часть 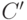 , равномощную
, равномощную  , и
положим
, и
положим 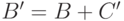 (рис. рис. 11.2).
(рис. рис. 11.2).
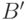 равномощны
равномощны  . Поэтому
. Поэтому  разбивается
на
разбивается
на 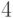 части, каждая из которых равномощна
части, каждая из которых равномощна  , и, следовательно,
равномощна
, и, следовательно,
равномощна  (напомним, что у нас есть
взаимно однозначное соответствие
(напомним, что у нас есть
взаимно однозначное соответствие  между
между  и
и  ).
Соответствие
).
Соответствие  можно продолжить до соответствия
можно продолжить до соответствия 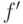 между
между 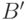 и
и  , дополнив его соответствием между
, дополнив его соответствием между 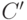 и
и 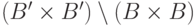 (эта разность
состоит из трех
множеств, равномощных
(эта разность
состоит из трех
множеств, равномощных  , так что равномощна
, так что равномощна  ).
В итоге мы получаем большую пару
).
В итоге мы получаем большую пару 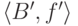 ,
что противоречит утверждению леммы Цорна о максимальности.
Таким образом, этот случай невозможен.
,
что противоречит утверждению леммы Цорна о максимальности.
Таким образом, этот случай невозможен.Выведем теперь некоторые следствия из доказанного утверждения.
Теорема 35.
(а)
Произведение двух
бесконечных мощностей равно большей из них.
(б)
Если множество  бесконечно, то множество
бесконечно, то множество 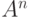 всех
последовательностей длины
всех
последовательностей длины 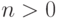 , составленных из
элементов
, составленных из
элементов  ,
равномощно
,
равномощно  .
(в)
Если множество
.
(в)
Если множество  бесконечно, то множество всех конечных
последовательностей, составленных из элементов
бесконечно, то множество всех конечных
последовательностей, составленных из элементов  ,
равномощно
,
равномощно  .
.
Доказательство.
Первое утверждение доказывается просто: если 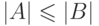 ,
то
,
то  .
.
Второе утверждение легко доказывается индукцией по  : если
: если  , то
, то 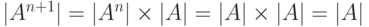 .
.
Третье тоже просто: множество конечных последовательностей
есть 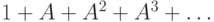 ; каждая из
частей (кроме первой, которой можно пренебречь) равномощна
; каждая из
частей (кроме первой, которой можно пренебречь) равномощна  (по доказанному), и потому все вместе
есть
(по доказанному), и потому все вместе
есть  .
.
Заметим, что из последнего утверждения теоремы вытекает, что
семейство всех конечных подмножеств бесконечного множества  имеет ту же мощность, что и
имеет ту же мощность, что и  (подмножеств не больше, чем
конечных последовательностей и не меньше, чем одноэлементных
подмножеств).
(подмножеств не больше, чем
конечных последовательностей и не меньше, чем одноэлементных
подмножеств).
122. Пусть  бесконечно. Докажите, что
бесконечно. Докажите, что  .
.
123. Рассмотрим мощность 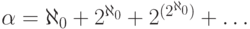 (счетная сумма). Покажите, что
(счетная сумма). Покажите, что  - минимальная мощность,
которая больше мощностей множеств
- минимальная мощность,
которая больше мощностей множеств  ,
, 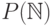 ,
,  ,
,  Покажите, что
Покажите, что  .
.
Теперь мы можем доказать упоминавшееся ранее утверждение о равномощности базисов.
Теорема 36. Любые два базиса в бесконечномерном векторном пространстве имеют одинаковую мощность.
Доказательство.
Пусть даны два базиса - первый и второй. Для каждого вектора
из первого базиса фиксируем какой-либо способ выразить его
через векторы второго базиса. В этом выражении участвует
конечное множество векторов второго базиса. Таким образом,
есть некоторая функция, которая каждому вектору первого
базиса ставит в соответствие некоторое конечное множество
векторов второго. Как мы только что видели, возможных значений этой
функции столько же, сколько элементов во втором базисе.
Кроме того, прообраз каждого значения состоит из векторов
первого базиса, выражающихся через данный (конечный) набор векторов
второго, и потому конечен. Выходит, что первый базис
разбит на группы, каждая группа конечна, а всего групп не
больше, чем векторов во втором базисе. Поэтому
мощность первого базиса не превосходит мощности второго,
умноженной на 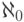 (от чего, как мы знаем, мощность
бесконечного множества не меняется). Осталось провести симметричное
рассуждение и сослаться на теорему Кантора- Бернштейна.
(от чего, как мы знаем, мощность
бесконечного множества не меняется). Осталось провести симметричное
рассуждение и сослаться на теорему Кантора- Бернштейна.

