Лемма Цорна и свойства операций
Свойства операций над мощностями
Теперь мы можем доказать несколько утверждений о мощностях.
Теорема 32.
Если  бесконечно, то
множество
бесконечно, то
множество  равномощно
равномощно  .
.
Доказательство.
Вполне упорядочим множество  . Мы уже знаем
, что всякий элемент множества
. Мы уже знаем
, что всякий элемент множества  однозначно представляется в виде
однозначно представляется в виде  , где
, где  -
предельный
элемент (не имеющий непосредственно предыдущего), а
-
предельный
элемент (не имеющий непосредственно предыдущего), а  -
натуральное число. Это означает, что
-
натуральное число. Это означает, что  равномощно
равномощно  ,
где
,
где  - множество предельных элементов. (Тут есть небольшая
трудность - последняя группа элементов
конечна, если в множестве есть наибольший элемент. Но мы уже знаем,
что добавление конечного или счетного множества не меняет
мощности, так что этим можно пренебречь.)
- множество предельных элементов. (Тут есть небольшая
трудность - последняя группа элементов
конечна, если в множестве есть наибольший элемент. Но мы уже знаем,
что добавление конечного или счетного множества не меняет
мощности, так что этим можно пренебречь.)
Теперь утверждение теоремы
очевидно:  равномощно
равномощно  , то есть
, то есть  и тем самым
и тем самым  (произведение счетных множеств
счетно), то есть
(произведение счетных множеств
счетно), то есть  .
.
По теореме Кантора -
Бернштейна
отсюда следует, что
промежуточные мощности (в частности,  , а также любое
произведение
, а также любое
произведение  и конечного
множества) совпадают с
и конечного
множества) совпадают с 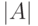 . Еще одно следствие полезно
выделить:
. Еще одно следствие полезно
выделить:
Теорема 33. Сумма двух бесконечных мощностей равна их максимуму.
Доказательство.
Прежде всего напомним, что любые две мощности сравнимы
(теорема 25). Пусть, скажем,  .
Тогда
.
Тогда  (последнее неравенство - утверждение
предыдущей теоремы). Остается воспользоваться теоремой Кантора-
Бернштейна и заключить, что
(последнее неравенство - утверждение
предыдущей теоремы). Остается воспользоваться теоремой Кантора-
Бернштейна и заключить, что 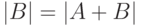 .
.
Теперь можно доказать более сильное утверждение.
Теорема 34.
Если  бесконечно, то
бесконечно, то  равномощно
равномощно  .
.
Доказательство.
Заметим, что для счетного множества (как, впрочем, и для
континуума - но это сейчас не важно) мы это уже знаем.
Поэтому в  есть подмножество, равномощное своему
квадрату.
есть подмножество, равномощное своему
квадрату.
Рассмотрим семейство всех таких подмножеств вместе с
соответствующими биекциями. Элементами этого семейства будут
пары  , где
, где  -
подмножество
-
подмножество  , а
, а  - взаимно однозначное соответствие.
Введем на
этом семействе частичный порядок:
- взаимно однозначное соответствие.
Введем на
этом семействе частичный порядок:  , если
, если  и
ограничение
отображения
и
ограничение
отображения 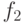 на
на 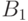 совпадает с
совпадает с 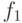 (рис. рис.11.1).
(рис. рис.11.1).
Отображение 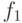 - взаимно однозначное соответствие
между малым квадратом и его стороной;
- взаимно однозначное соответствие
между малым квадратом и его стороной; 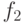 добавляет к нему
взаимно однозначное соответствие между
добавляет к нему
взаимно однозначное соответствие между  и
" уголком"
и
" уголком"  .
.
Теперь применим лемму Цорна. Для этого нужно убедиться, что любое
линейно упорядоченное (в смысле описанного порядка) множество
пар указанного вида имеет верхнюю границу. В самом деле,
объединим все первые компоненты
этих пар; пусть  - их
объединение. Как обычно, согласованность отображений
(гарантируемая определением порядка) позволяет соединить
отображения в одно. Это отображение (назовем его
- их
объединение. Как обычно, согласованность отображений
(гарантируемая определением порядка) позволяет соединить
отображения в одно. Это отображение (назовем его  )
отображает
)
отображает  в
в  . Оно будет инъекцией: значения
. Оно будет инъекцией: значения  и
и  при различных
при различных 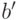 и
и 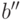 различны (возьмем большее
из множеств, которым принадлежат
различны (возьмем большее
из множеств, которым принадлежат 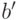 и
и 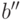 ; на нем
; на нем  является
инъекцией по предположению). С другой стороны,
является
инъекцией по предположению). С другой стороны,  является
сюръекцией: для любой пары
является
сюръекцией: для любой пары  возьмем множества, из которых произошли
возьмем множества, из которых произошли 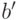 и
и 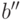 ,
выберем
из них большее и вспомним, что мы имели взаимно однозначное
соответствие между ним и его квадратом.
,
выберем
из них большее и вспомним, что мы имели взаимно однозначное
соответствие между ним и его квадратом.

