Лемма Цорна и свойства операций
Теорема 31. Всякий частичный порядок может быть продолжен до линейного.
Доказательство.
Пусть  - частично упорядоченное множество. Теорема
утверждает, что существует отношение порядка
- частично упорядоченное множество. Теорема
утверждает, что существует отношение порядка 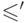 на
на  ,
продолжающее исходное (это значит, что
,
продолжающее исходное (это значит, что  ) и являющееся отношением линейного порядка. (Кстати,
отметим, что слово "линейного" в формулировке теоремы
нельзя заменить на слово "полного" - например, если исходный
порядок линейный, но не полный.)
) и являющееся отношением линейного порядка. (Кстати,
отметим, что слово "линейного" в формулировке теоремы
нельзя заменить на слово "полного" - например, если исходный
порядок линейный, но не полный.)
Готовясь к применению леммы Цорна, рассмотрим частично
упорядоченное множество  , элементами которого будут частичные
порядки на
, элементами которого будут частичные
порядки на  (то есть подмножества множества
(то есть подмножества множества  , обладающие
свойствами рефлексивности, транзитивности и антисимметричности),
упорядоченные по включению:
, обладающие
свойствами рефлексивности, транзитивности и антисимметричности),
упорядоченные по включению: 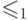 считается меньшим или
равным
считается меньшим или
равным  , если
, если  продолжает
продолжает 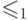 (из
(из  следует
следует  ).
).
Легко проверить, что условие леммы Цорна выполнено: если
у нас есть семейство частичных порядков, линейно упорядоченное
по включению, то объединение этих порядков является частичным
порядком, и этот порядок будет верхней границей семейства.
(Проверим, например, что объединение обладает свойством
транзитивности. Пусть  в одном из порядков семейства
в одном из порядков семейства 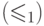 ,
а
,
а  в другом; один из порядков
(например,
в другом; один из порядков
(например, 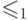 ) продолжает
другой, тогда
) продолжает
другой, тогда 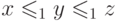 и потому
и потому  в
объединении.
Рефлексивность и антисимметричность проверяются столь же просто.)
в
объединении.
Рефлексивность и антисимметричность проверяются столь же просто.)
Следовательно, по лемме Цорна на множестве  существует
максимальный частичный порядок, продолжающий
исходный. Обозначим
его как
существует
максимальный частичный порядок, продолжающий
исходный. Обозначим
его как 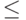 (путаницы с исходным порядком не возникнет,
так как исходный нам больше не нужен). Нам надо показать, что он
будет линейным. Пусть
(путаницы с исходным порядком не возникнет,
так как исходный нам больше не нужен). Нам надо показать, что он
будет линейным. Пусть  - два несравнимых элемента. Расширим порядок до
нового порядка
- два несравнимых элемента. Расширим порядок до
нового порядка 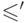 , при котором
, при котором  . Этот новый
порядок
определяется так:
. Этот новый
порядок
определяется так:  , если (1)
, если (1)  или (2)
или (2)  и
и 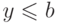 .
Несложно проверить, что
.
Несложно проверить, что 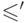 будет
частичным порядком. Рефлексивность очевидна. Транзитивность:
если
будет
частичным порядком. Рефлексивность очевидна. Транзитивность:
если  и
и  , то есть четыре возможности.
Если в
обоих случаях имеет место случай (1), то
, то есть четыре возможности.
Если в
обоих случаях имеет место случай (1), то 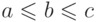 и все
очевидно. Если
и все
очевидно. Если  в силу (1), а
в силу (1), а  в
силу (2), то
в
силу (2), то 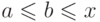 и
и  , так что
, так что  в силу (2).
Аналогично рассматривается и симметричный случай. Наконец,
двукратная ссылка на (2) невозможна, так как тогда
в силу (2).
Аналогично рассматривается и симметричный случай. Наконец,
двукратная ссылка на (2) невозможна, так как тогда 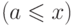 ,
, 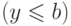 ,
, 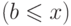 и
и 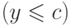 ,
и получается, что
,
и получается, что 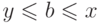 ,
а мы предполагали, что
,
а мы предполагали, что  и
и  не сравнимы.
Антисимметричность
доказывается аналогично. Таким образом, отношение
не сравнимы.
Антисимметричность
доказывается аналогично. Таким образом, отношение 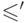 будет
частичным порядком, строго содержащим
будет
частичным порядком, строго содержащим 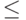 , что противоречит
максимальности.
, что противоречит
максимальности.
120. Покажите, что любое бинарное отношение без циклов (цикл
образуется, если  , или
, или 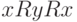 , или
, или 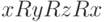 и т.д) может
быть продолжено до линейного порядка. (Для конечных множеств
поиск такого продолжения обычно называют " топологической
сортировкой ".)
и т.д) может
быть продолжено до линейного порядка. (Для конечных множеств
поиск такого продолжения обычно называют " топологической
сортировкой ".)
121. Множество на плоскости называется выпуклым, если вместе с любыми
двумя точками оно содержит соединяющий их отрезок. Покажите, что
любые два непересекающихся выпуклых множества можно разделить прямой
(каждое множество лежит по одну сторону от прямой, возможно, пересекаясь
с ней). (Указание. Используя лемму Цорна, можно расширить исходные
непересекающиеся множества  и
и  до взаимно
дополнительных
выпуклых множеств
до взаимно
дополнительных
выпуклых множеств 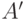 и
и 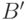 . Затем можно убедиться, что
граница между
. Затем можно убедиться, что
граница между 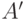 и
и 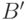 представляет собой прямую.)
представляет собой прямую.)
