Фундированные и вполне упорядоченные множества
Фундированные множества
Принцип математической индукции в одной из возможных форм звучит так:
Пусть
- некоторое свойство натурального числа
. Пусть нам удалось доказать
в предположении, что
верно для всех
, меньших
. Тогда свойство
верно для всех натуральных чисел
.
(Заметим, что по условию доказательство 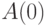 возможно без
всяких
предположений, поскольку меньших чисел нет.)
возможно без
всяких
предположений, поскольку меньших чисел нет.)
Для каких частично упорядоченных множеств верен аналогичный принцип? Ответ дается следующей простой теоремой:
Теорема 15.
Следующие три свойства частично упорядоченного множества  равносильны:
равносильны:
(a) любое непустое подмножество  имеет минимальный
элемент;
имеет минимальный
элемент;
(б) не существует бесконечной строго убывающей
последовательности  элементов
множества
элементов
множества  ;
;
(в) для множества  верен принцип индукции в следующей
форме: если (при каждом
верен принцип индукции в следующей
форме: если (при каждом 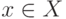 )
из истинности
)
из истинности 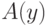 для всех
для всех 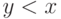 следует
истинность
следует
истинность 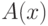 ,
то свойство
,
то свойство 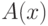 верно при всех
верно при всех  .
Формально это записывают так:
.
Формально это записывают так:
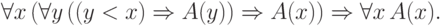
Доказательство.
Сначала докажем эквивалентность первых двух свойств. Если  - бесконечная убывающая
последовательность,
то, очевидно, множество ее значений не имеет минимального
элемента (для каждого элемента следующий еще меньше).
Поэтому из (а) следует (б). Напротив, если
- бесконечная убывающая
последовательность,
то, очевидно, множество ее значений не имеет минимального
элемента (для каждого элемента следующий еще меньше).
Поэтому из (а) следует (б). Напротив, если  - непустое
множество, не имеющее минимального элемента, то бесконечную
убывающую последовательность можно построить так. Возьмем
произвольный элемент
- непустое
множество, не имеющее минимального элемента, то бесконечную
убывающую последовательность можно построить так. Возьмем
произвольный элемент 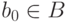 . По предположению
он не является минимальным, так что можно найти
. По предположению
он не является минимальным, так что можно найти 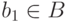 ,
для которого
,
для которого 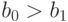 . По тем же причинам можно найти
. По тем же причинам можно найти 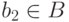 ,
для которого
,
для которого 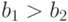 и т.д. Получается бесконечная убывающая
последовательность.
и т.д. Получается бесконечная убывающая
последовательность.
Теперь выведем принцип индукции из существования минимального
элемента в любом подмножестве. Пусть 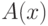 - произвольное
свойство элементов множества
- произвольное
свойство элементов множества  , верное не для всех
элементов
, верное не для всех
элементов  .
Рассмотрим непустое множество
.
Рассмотрим непустое множество  тех элементов, для
которых свойство
тех элементов, для
которых свойство  неверно. Пусть
неверно. Пусть  - минимальный
элемент
множества
- минимальный
элемент
множества  .
По условию меньших элементов в множестве
.
По условию меньших элементов в множестве  нет,
поэтому для всех
нет,
поэтому для всех 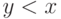 свойство
свойство 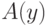 выполнено. Но
тогда по
предположению должно быть выполнено и
выполнено. Но
тогда по
предположению должно быть выполнено и 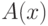 -
противоречие.
-
противоречие.
Осталось доказать существование минимального элемента в любом
непустом подмножестве, исходя из принципа индукции. Пусть  -
подмножество без минимальных элементов. Докажем по
индукции, что
-
подмножество без минимальных элементов. Докажем по
индукции, что  пусто; другими словами, в
качестве
пусто; другими словами, в
качестве 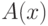 возьмем свойство
возьмем свойство 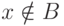 . В самом деле, если
. В самом деле, если 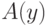 верно
для всех
верно
для всех 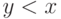 , то никакой элемент, меньший
, то никакой элемент, меньший  , не
лежит в
, не
лежит в  . Если бы
. Если бы  лежал в
лежал в  , то он
был бы там минимальным, а таких нет.
, то он
был бы там минимальным, а таких нет.
Множества, обладающие свойствами (а)-(в), называются фундированными. Какие есть примеры фундированных множеств? Прежде всего, наш исходный пример - множество натуральных чисел.
Другой пример - множество  пар натуральных чисел (меньше та пара, у которой второй
член меньше; в случае равенства сравниваем первые).
В самом деле, проверим условие (б). Нам будет удобно
сформулировать его так: всякая последовательность
пар натуральных чисел (меньше та пара, у которой второй
член меньше; в случае равенства сравниваем первые).
В самом деле, проверим условие (б). Нам будет удобно
сформулировать его так: всякая последовательность  элементов множества
рано или поздно стабилизируется (все члены, начиная с
некоторого, равны); очевидно, что это эквивалентная
формулировка.
элементов множества
рано или поздно стабилизируется (все члены, начиная с
некоторого, равны); очевидно, что это эквивалентная
формулировка.
Пусть дана произвольная последовательность пар
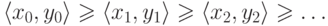
 и потому последовательность
натуральных чисел
и потому последовательность
натуральных чисел  с какого - то места не меняется. После этого уже
с какого - то места не меняется. После этого уже  должны
убывать - и тоже стабилизируются. Что и требовалось.
должны
убывать - и тоже стабилизируются. Что и требовалось.То же самое рассуждение пригодно и в более общей ситуации.
Теорема 16.
Пусть  и
и  - два фундированных частично
упорядоченных
множества. Тогда их произведение
- два фундированных частично
упорядоченных
множества. Тогда их произведение  , в котором
, в котором
![\langle a_1, b_1 \rangle \le
\langle a_2, b_2 \rangle \Leftrightarrow
[(b_1 \hm< b_2) \text{ или } (b_1=b_2 \text{ и } a_1\le a_2)],](/sites/default/files/tex_cache/fb97031392d9f3382cfbc1d45d3d1c8e.png)
Доказательство.
В последовательности 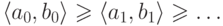 стабилизируются сначала
вторые, а затем и первые члены.
стабилизируются сначала
вторые, а затем и первые члены.
Отсюда вытекает аналогичное утверждение
для  ,
для
,
для  или вообще для произведения конечного числа фундированных
множеств.
или вообще для произведения конечного числа фундированных
множеств.
Еще проще доказать, что сумма  двух фундированных множеств
двух фундированных множеств  и
и  фундирована: последовательность
фундирована: последовательность  либо целиком содержится в
либо целиком содержится в  (и мы ссылаемся на
фундированность
(и мы ссылаемся на
фундированность  ), либо содержит элемент из
), либо содержит элемент из  . В
последнем
случае все следующие элементы также принадлежат
. В
последнем
случае все следующие элементы также принадлежат  , и мы
используем фундированность
, и мы
используем фундированность  .
.
Часто в программировании (или в олимпиадных задачах) нам нужно
доказать, что некоторый процесс не может продолжаться бесконечно
долго. Например, написав цикл, мы должны убедиться, что рано или
поздно из него выйдем. Это можно сделать так: ввести какой - то
натуральный параметр и убедиться, что на каждом шаге цикла этот
параметр уменьшается. Тогда, если сейчас этот параметр равен  ,
то можно гарантировать, что не позже чем через
,
то можно гарантировать, что не позже чем через  шагов
цикл закончится.
шагов
цикл закончится.
Однако бывают ситуации, в которых число шагов заранее оценить нельзя, но тем не менее гарантировать завершение цикла можно, поскольку есть параметр, принимающий значения в фундированном множестве и убывающий на каждом шаге цикла.
Вот пример олимпиадной задачи, где по существу такое рассуждение и используется.
Задача. Бизнесмен заключил с чертом сделку: каждый день он дает черту одну монету, и в обмен получает любой набор монет по своему выбору, но все эти монеты меньшего достоинства (видов монет конечное число). Менять (или получать) деньги в другом месте бизнесмен не может. Когда монет больше не останется, бизнесмен проигрывает. Докажите, что рано или поздно черт выиграет, каков бы ни был начальный набор монет у бизнесмена.
Решение: пусть имеется  видов монет. Искомый параметр
определим так: посчитаем, сколько монет каждого вида есть у
бизнесмена (
видов монет. Искомый параметр
определим так: посчитаем, сколько монет каждого вида есть у
бизнесмена ( 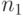 - число монет минимального достоинства,
- число монет минимального достоинства, 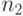 - число следующих, и так далее до
- число следующих, и так далее до 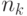 ). Заметим,
что в
результате встречи с чертом набор
). Заметим,
что в
результате встречи с чертом набор 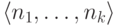 уменьшается (в смысле введенного нами порядка, когда мы
сравниваем сначала последние члены, затем предпоследние \итд).
Поскольку множество
уменьшается (в смысле введенного нами порядка, когда мы
сравниваем сначала последние члены, затем предпоследние \итд).
Поскольку множество 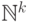 фундировано, этот процесс должен
оборваться.
фундировано, этот процесс должен
оборваться.
108. Имеется конечная последовательность нулей и единиц. За один
шаг разрешается сделать такое действие: найти в ней группу 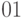 и заменить на
и заменить на 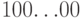 (при этом можно написать сколько
угодно нулей). Докажите, что такие шаги нельзя выполнять бесконечно
много раз.
(при этом можно написать сколько
угодно нулей). Докажите, что такие шаги нельзя выполнять бесконечно
много раз.
109. Рассмотрим множество всех слов русского алфавита (точнее, всех конечных последовательностей русских букв, независимо от смысла) с лексикографическим порядком. Будет ли это множество фундировано?
110. Рассмотрим множество невозрастающих последовательностей натуральных чисел, в которых все члены, начиная с некоторого, равны нулю. Введем в нем порядок так: сначала сравниваем первые члены, при равенстве первых вторые и т.д. Докажите, что это (линейно) упорядоченное множество фундировано.
111. Рассмотрим множество всех многочленов от одной переменной  ,
коэффициенты которых - натуральные числа. Упорядочим его так:
многочлен
,
коэффициенты которых - натуральные числа. Упорядочим его так:
многочлен  больше многочлена
больше многочлена  , если
, если 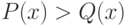 для
всех достаточно больших
для
всех достаточно больших  . Покажите, что это определение
задает линейный порядок и что получающееся упорядоченное
множество фундировано.
. Покажите, что это определение
задает линейный порядок и что получающееся упорядоченное
множество фундировано.
