Фундированные и вполне упорядоченные множества
Вполне упорядоченные множества
Фундированные линейно упорядоченные множества называются вполне упорядоченными, а соответствующие порядки - полными. Для линейных порядков понятия наименьшего и минимального элемента совпадают, так что во вполне упорядоченном множестве всякое непустое подмножество имеет наименьший элемент.
Заметим, что частично упорядоченное множество, в котором всякое непустое подмножество имеет наименьший элемент, автоматически является линейно упорядоченным (в самом деле, всякое двухэлементное множество имеет наименьший элемент, поэтому любые два элемента сравнимы).
Примеры вполне упорядоченных множеств:  ,
,  (здесь
(здесь  обозначает конечное линейно
упорядоченное множество из
обозначает конечное линейно
упорядоченное множество из  элементов),
элементов),  ,
,  .
.
Наша цель - понять, как могут быть устроены вполне упорядоченные множества. Начнем с нескольких простых замечаний.
- Вполне упорядоченное множество имеет наименьший элемент. (Непосредственное следствие определения.)
- Для каждого элемента
 вполне упорядоченного множества (кроме
наибольшего) есть непосредственно следующий за ним элемент
вполне упорядоченного множества (кроме
наибольшего) есть непосредственно следующий за ним элемент  (это значит, что
(это значит, что  , но не существует
, но не существует  , для
которого
, для
которого 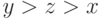 ). В самом деле, если множество всех
элементов,
больших
). В самом деле, если множество всех
элементов,
больших  , непусто, то в нем есть минимальный
элемент
, непусто, то в нем есть минимальный
элемент  ,
который и будет искомым. Такой элемент логично обозначать
,
который и будет искомым. Такой элемент логично обозначать 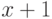 ,
следующий за ним -
,
следующий за ним -  и т.д.
и т.д. - Некоторые элементы вполне упорядоченного множества могут не иметь
непосредственно предыдущего. Например, в
множестве
 есть два элемента, не имеющих
непосредственно предыдущего (наименьший элемент, а также
наименьший элемент второй копии натурального ряда). Такие
элементы называют предельными.
есть два элемента, не имеющих
непосредственно предыдущего (наименьший элемент, а также
наименьший элемент второй копии натурального ряда). Такие
элементы называют предельными. - Всякий элемент упорядоченного множества имеет вид
 , где
, где  - предельный, а
- предельный, а  - натуральное число
(обозначение
- натуральное число
(обозначение  понимается в описанном выше смысле). В самом деле, если
понимается в описанном выше смысле). В самом деле, если  не
предельный, возьмем предыдущий, если и он непредельный -
то его предыдущий и т.д., пока не дойдем до предельного
(бесконечно продолжаться это не может, так как множество вполне
упорядочено). Очевидно, такое представление однозначно
(у элемента может быть только один непосредственно предыдущий).
не
предельный, возьмем предыдущий, если и он непредельный -
то его предыдущий и т.д., пока не дойдем до предельного
(бесконечно продолжаться это не может, так как множество вполне
упорядочено). Очевидно, такое представление однозначно
(у элемента может быть только один непосредственно предыдущий). - Любое ограниченное сверху множество элементов вполне упорядоченного
множества имеет точную верхнюю грань.
(Как обычно, подмножество
 частично
упорядоченного множества
частично
упорядоченного множества  называется ограниченным сверху,
если оно имеет верхнюю границу,
т.е. элемент
называется ограниченным сверху,
если оно имеет верхнюю границу,
т.е. элемент 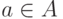 ,
для которого
,
для которого 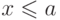 при всех
при всех 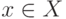 . Если среди
всех верхних границ данного подмножества есть наименьшая, то она
называется точной верхней гранью.)
. Если среди
всех верхних границ данного подмножества есть наименьшая, то она
называется точной верхней гранью.)В самом деле, множество всех верхних границ непусто и потому имеет наименьший элемент. (Заметим в скобках, что вопрос о точной нижней грани для вполне упорядоченного множества тривиален, так как всякое множество имеет наименьший элемент.)
Пусть  - произвольное вполне упорядоченное множество. Его
наименьший элемент обозначим через
- произвольное вполне упорядоченное множество. Его
наименьший элемент обозначим через  . Следующий за ним элемент
обозначим через
. Следующий за ним элемент
обозначим через  , следующий за
, следующий за  -
через
-
через  и т.д. Если
множество конечно, процесс этот оборвется. Если бесконечно,
посмотрим, исчерпали ли мы все элементы множества
и т.д. Если
множество конечно, процесс этот оборвется. Если бесконечно,
посмотрим, исчерпали ли мы все элементы множества  . Если нет,
возьмем минимальный элемент из оставшихся. Обозначим его
. Если нет,
возьмем минимальный элемент из оставшихся. Обозначим его  .
Следующий за ним элемент (если он есть) обозначим
.
Следующий за ним элемент (если он есть) обозначим  ,
затем
,
затем  и т.д Если и на этом множество не
исчерпается, то возьмем наименьший элемент из оставшихся,
назовем его
и т.д Если и на этом множество не
исчерпается, то возьмем наименьший элемент из оставшихся,
назовем его 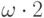 ,
и повторим всю процедуру. Затем
будут
,
и повторим всю процедуру. Затем
будут 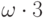 ,
, 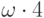 и т.д Если и
на этом множество не
кончится, минимальный из оставшихся элементов назовем
и т.д Если и
на этом множество не
кончится, минимальный из оставшихся элементов назовем 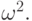 Затем
пойдут
Затем
пойдут 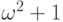 ,
, 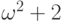 ,
,  ,
, 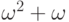 ,
,  ,
, 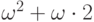 ,
,  ,
, 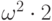 ,
,  ,
, 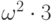 ,
,  ,
, 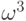 ,
,  (мы не поясняем сейчас подробно обозначения).
(мы не поясняем сейчас подробно обозначения).
Что, собственно говоря, доказывает это рассуждение? Попытаемся
выделить некоторые утверждения. При этом полезно
такое определение: если линейно упорядоченное множество  разбито на две (непересекающиеся) части
разбито на две (непересекающиеся) части  и
и  ,
причем любой
элемент
,
причем любой
элемент  меньше любого элемента
меньше любого элемента  , то
, то  называют начальным отрезком множества
называют начальным отрезком множества  .
Другими словами,
подмножество
.
Другими словами,
подмножество  линейно упорядоченного множества
линейно упорядоченного множества  является
начальным отрезком, если любой элемент
является
начальным отрезком, если любой элемент  меньше любого
элемента
меньше любого
элемента  . Еще одна переформулировка:
. Еще одна переформулировка: 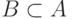 является начальным отрезком, если из
является начальным отрезком, если из  ,
, 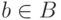 и
и  следует
следует 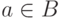 . Заметим, что
начальный отрезок
может быть пустым или совпадать со всем множеством.
. Заметим, что
начальный отрезок
может быть пустым или совпадать со всем множеством.
Отметим сразу же несколько простых свойств начальных отрезков:
- Начальный отрезок вполне упорядоченного множества (как, впрочем, и любое подмножество) является вполне упорядоченным множеством.
- Начальный отрезок начального отрезка есть начальный отрезок исходного множества.
- Объединение любого семейства начальных отрезков (в одном и том же упорядоченном множестве) есть начальный отрезок того же множества.
- Если
 - произвольный элемент вполне упорядоченного
множества
- произвольный элемент вполне упорядоченного
множества  , то множества
, то множества 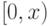 (все элементы
множества
(все элементы
множества  ,
меньшие
,
меньшие  ) и
) и ![[0,x]](/sites/default/files/tex_cache/47e2767cb741a37b889f1968c34f8398.png) (элементы
множества
(элементы
множества  , меньшие или
равные
, меньшие или
равные  ) являются начальными отрезками.
) являются начальными отрезками. - Всякий начальный отрезок
 вполне упорядоченного
множества
вполне упорядоченного
множества  , не совпадающий со всем множеством, имеет
вид
, не совпадающий со всем множеством, имеет
вид 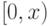 для некоторого
для некоторого 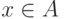 . (В самом деле, если
. (В самом деле, если  , возьмем наименьший элемент
, возьмем наименьший элемент  в
множестве
в
множестве 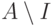 .
Тогда все меньшие элементы принадлежат
.
Тогда все меньшие элементы принадлежат  , сам
, сам  не
принадлежит
не
принадлежит  и все б\'ольшие
и все б\'ольшие  элементы не
принадлежат
элементы не
принадлежат  ,
иначе получилось бы противоречие с определением начального
отрезка.)
,
иначе получилось бы противоречие с определением начального
отрезка.) - Любые два начальных отрезка вполне упорядоченного множества сравнимы по включению,т.е. один есть подмножество другого. (Следует из предыдущего.)
- Начальные отрезки вполне упорядоченного множества
 ,
упорядоченные по включению, образуют вполне упорядоченное
множество. Это множество состоит из наибольшего элемента
(все
,
упорядоченные по включению, образуют вполне упорядоченное
множество. Это множество состоит из наибольшего элемента
(все  ) и остальной части, изоморфной множеству
) и остальной части, изоморфной множеству  .
(В самом
деле, начальные отрезки множества
.
(В самом
деле, начальные отрезки множества  , не совпадающие
с
, не совпадающие
с  ,
имеют вид
,
имеют вид 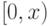 , и соответствие
, и соответствие 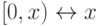 будет
изоморфизмом.)
будет
изоморфизмом.)
Возвратимся к нашему рассуждению с последовательным выделением
различных элементов из вполне упорядоченного множества. Его
первую часть можно считать доказательством такого утверждения:
если вполне упорядоченное множество бесконечно, то оно имеет
начальный отрезок, изоморфный  . (Говоря о множестве
натуральных чисел вместе с порядком, обычно употребляют
обозначение
. (Говоря о множестве
натуральных чисел вместе с порядком, обычно употребляют
обозначение  , а
не
, а
не  .)
.)
Но на этом наше рассуждение не оканчивается. Его следующая часть
может считаться доказательством такого факта: либо  изоморфно
некоторому начальному отрезку множества
изоморфно
некоторому начальному отрезку множества 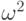 , либо оно
имеет начальный отрезок, изоморфный
, либо оно
имеет начальный отрезок, изоморфный 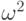 . (Здесь
. (Здесь 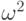 - вполне упорядоченное
множество пар натуральных
чисел: сравниваются сначала вторые компоненты пар, а при их
равенстве - первые.)
- вполне упорядоченное
множество пар натуральных
чисел: сравниваются сначала вторые компоненты пар, а при их
равенстве - первые.)
Вообще верно такое утверждение: для любых двух вполне упорядоченных множеств одно изоморфно начальному отрезку другого, и доказательство состоит более или менее в повторении проведенного рассуждения. Но чтобы сделать это аккуратно, нужна некоторая подготовка.
