Лекция 12: Оптимизация при наличии ограничений. Ограничения в виде равенств. Ограничения в виде неравенств. Выпуклость и вогнутость. Комплексный метод
4. Комплексный метод
Трудности, встречающиеся при попытке использовать существовавшие
ранее методы поиска, подтолкнули Бокса в 1964 году к созданию
своего метода. По существу, он является модификацией симплексного
метода Нелдера - Мида, однако позволяет учитывать ограничения. Бокс
назвал его комплексным методом. Решаемая задача состоит в
минимизации функции f(х) = f(x1, х2, ..., хn),
где  определяется явными ограничениями
определяется явными ограничениями
 |
( 4.1) |
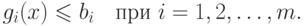
Если целевая функция f(х) выпукла и функции gi(x) тоже выпуклы, то задача будет иметь единственное решение. Значения lj и uj являются нижней и верхней границами переменных. Если в конкретной задаче заданные переменные теоретически не имеют ограничений, то предположение о наличии у них "безопасных" границ, т.е. границ, включающих оптимум, позволит применить комплексный метод.
Данный метод является итерационным. В нем предполагается, что известны значения n и m, lj и uj и начальная точка x1, удовлетворяющая всем ограничениям (см. неравенства (4.1) и (4.2)). В первую очередь необходимо выбрать к точек, которые удовлетворяют ограничениям, а также вычислить целевую функцию во всех k точках. Множество этих точек называется комплексом. Бокс обнаружил, что k должно быть больше (n + 1) - числа точек, используемых в симплексном методе Нелдера-Мида и положил k = 2n.
Как упоминалось выше, предполагается, что точка k1, удовлетворяющая всем ограничениям, задана. Остальные точки, удовлетворяющие неравенству (4.1), могут быть выбраны следующим образом:
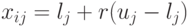 |
( 4.3) |
для j = 1,2,...,n и i = 2,3,...,k, где r - псевдослучайная равномерно распределенная переменная в интервале (0;1).
Точки, выбираемые в соответствии с уравнением (4.3) для данного j будут автоматически удовлетворять неравенству (4.1). Если эти точки удовлетворяют также неравенству (4.2), то они принимаются в качестве начальных точек комплекса. Если точка, выбранная в соответствии с уравнением (4.3), не удовлетворяет неравенству (4.2), то она смещается на половину расстояния до центра тяжести множества уже принятых точек, т.е. формируется точка
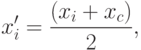 |
( 4.4) |
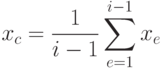 |
( 4.5) |
Если точка в соотношении (4.4) все еще не является допустимой, то описанная соотношением (4.3) процедура повторяется вновь до тех пор, пока точка не станет допустимой. Если функция gi(x) выпукла, то в конце концов ограничения будут выполняться. Конечно, поскольку точка x1 находится внутри области ограничений, то комплекс будет состоять из допустимых точек.
Удобно упорядочить точки комплекса в соответствии со значениями функции. Процедуру инициализации комплекса можно описать с помощью блок-схемы (рис. 12.5).
Теперь мы подошли к итерационной процедуре комплексного метода, в которой производится поиск минимума перемещением по направлению к минимуму внутри области ограничений. Для этой процедуры необходимы следующие шаги:
1. Найти точку с наибольшим значением функции xh и найти центр x0 остальных (k - 1) точек.
2. Попытаемся сместиться от точки xh и
получить при этом точку xr, отражением точки xh относительно точки x0, используя коэффициент отражения  , что можно записать как
, что можно записать как
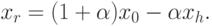 |
( 4.6) |
3. Проверить, является ли точка xr допустимой.
а). Если точка xr не является допустимой и не выполняется ограничение для lj, то полагаем xrj = lj + 10-6 ; если не выполняется ограничение для uj то полагаем xrj = uj - 10-6
б). Если не выполняются ограничения, то точку xr, перемещают на половину расстояния между xr и центром x0, т.е.
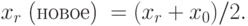 |
( 4.7) |
Затем производится повторная проверка на допустимость и шаг 3 повторяется до тех пор, пока не будет получена допустимая точка.
4. Если точка xr является допустимой, то вычисляется значение функции f(xr) и сравнивается с f(xk) - наибольшим значением функции.
Если f(хr) > f(xk), т.е. "хуже", чем наибольшее значение, полученное ранее, то точка xr смещается к центру x0 на половину расстояния между ними, т.е.
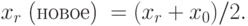
5. Если f(xr) < f(хk), то точка x заменяется на точку xr, затем точки и значения функции комплекса снова упорядочиваются.
6. Вычисляются две величины, использующиеся при проверке
сходимости метода: среднее квадратическое отклонение  для k значений функции и
максимальное расстояние dm между двумя точками
комплекса. Первая величина вычисляется как
для k значений функции и
максимальное расстояние dm между двумя точками
комплекса. Первая величина вычисляется как
![\sigma =
\left\{
\sum_{e=1}^k [f(x_e) - \bar{f}]^2 / k
\right\}^{1/2} ,](/sites/default/files/tex_cache/0f42435d0301d411d16c80f6a399f490.png) |
( 4.8) |
 |
( 4.9) |
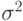 лучше использовать формулу
лучше использовать формулу![\sigma^2 =
\left. \left\{
\sum_{e=1}^k f(x_e)^2 - \frac{[\sum f(x)]^2}{k}
\right\} \right/ k.](/sites/default/files/tex_cache/bdc762c2e37eca17ac847ecc8a0a0595.png) |
( 4.10) |
7. Величины 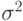 и dm проверяются
на сходимость. Если обе эти величины достаточно малы, то процедура
поиска минимума заканчивается. В противном случае необходимо
вернуться на шаг 1 и повторить процедуру.
и dm проверяются
на сходимость. Если обе эти величины достаточно малы, то процедура
поиска минимума заканчивается. В противном случае необходимо
вернуться на шаг 1 и повторить процедуру.
Процедура сходится, когда комплекс "стягивается" до такого размера, при котором он помещается в небольшой окрестности точки минимума. Проверка сходимости будет успешно заканчиваться на этом шаге, поскольку разница в значениях функции будет также мала.
Bы6op k = 2n и 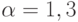 является
эмпирическим правилом, предложенным Боксом. Первое значение частично
предотвращает преждевременное сжатие комплекса. Коэффициент отражения
является
эмпирическим правилом, предложенным Боксом. Первое значение частично
предотвращает преждевременное сжатие комплекса. Коэффициент отражения  позволяет комплексу расширяться и
перемещаться в нужном направлении. Перемещения на половину расстояния
от начальной точки к центру сжимают комплекс. Поэтому комплекс может
перемещаться внутри допустимой области вдоль границ и огибать углы в
местах пересечения ограничений.
позволяет комплексу расширяться и
перемещаться в нужном направлении. Перемещения на половину расстояния
от начальной точки к центру сжимают комплекс. Поэтому комплекс может
перемещаться внутри допустимой области вдоль границ и огибать углы в
местах пересечения ограничений.
Способ выбора начального комплекса означает, что легко может быть сделано несколько перемещений. Очевидно, что будет сделано более одного перемещения даже в том случае, когда метод преждевременно сходится по причине какой-нибудь особенности используемых точек. Конечно, разумно получить некоторую информацию о значении минимума функции, чтобы для реально минимизируемой функции минимум был бы близок к нулю. Это позволит избежать любых осложнений в процессе вычисления погрешности при проверке на сходимость. Если из девяти цифр значения функции восемь первых цифр совпадают, то можно столкнуться с большими сложностями при определении точности и даже получить отрицательную разность при определении погрешности (это как раз будет машинная точность, но все равно в процессе вычисления появятся погрешности). Итак, установлено, что минимум функции действительно равен нулю.

