Лекция 13: Решение задач нелинейного программирования с ограничениями. Геометрическая интерпретация задач нелинейного программирования
В области нелинейного программирования с ограничениями ( условная оптимизация ) методы решения задач менее разработаны по сравнению с областью нелинейного программирования без ограничений (безусловная оптимизация). Здесь встречаются большие трудности по той же причине, что искомое решение должно подчиняться дополнительным требованиям, выраженных в виде ограничений.
1. Метод штрафных функций
Имеются несколько подходов при разработке методов решения задач нелинейного программирования с ограничениями. Для учета ограничений большое распространение получил метод штрафных функций.
Основная идея метода штрафной функции состоит в преобразовании задачи минимизации функции
z=f(x)
с соответствующими ограничениями, наложенными на x, в задачу поиска минимума без ограничений функции
Z=f(x)+P(x).
Функция Р(х) является штрафной. Необходимо, чтобы при нарушении ограничений она "штрафовала" функцию Z, т.е. увеличивала ее значение. В этом случае минимум Z будет находиться внутри области ограничений. Функция Р(х), удовлетворяющая этому условию, может быть не единственной. Задачу минимизации можно сформулировать следующим образом:
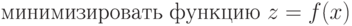 |
( 1.1) |
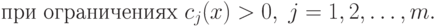 |
( 1.2) |
Замечание. Ограничение вида "меньше или равно", 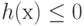 , всегда может быть записано как
, всегда может быть записано как 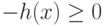 , поэтому в приведенной выше формулировке
нет потери общности.
, поэтому в приведенной выше формулировке
нет потери общности.
Функцию Р(х) удобно записать следующим образом:
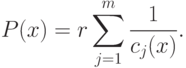 |
( 1.3) |
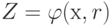 принимает вид
принимает вид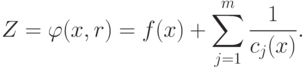 |
( 1.4) |
Если x принимает допустимые значения, т.е. значения,
для которых 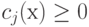 , то Z принимает
значения, которые больше соответствующих значений f(х)
(истинной целевой функции
данной задачи), и разность можно уменьшить
за счет того, что r может быть очень малой величиной.
Но если x принимает значения, которые хотя и являются
допустимыми, но близки к границе области ограничений, и по крайней
мере одна из функций cj(x) близка к нулю,
тогда значения функции Р(х) и, следовательно, значения
функции Z станут очень велики. Таким образом, влияние
функции Р(х) состоит в создании "гребня с крутыми
краями" вдоль каждой границы области ограничений. Следовательно,
если поиск начинается из допустимой точки и осуществляется поиск
минимума функции
, то Z принимает
значения, которые больше соответствующих значений f(х)
(истинной целевой функции
данной задачи), и разность можно уменьшить
за счет того, что r может быть очень малой величиной.
Но если x принимает значения, которые хотя и являются
допустимыми, но близки к границе области ограничений, и по крайней
мере одна из функций cj(x) близка к нулю,
тогда значения функции Р(х) и, следовательно, значения
функции Z станут очень велики. Таким образом, влияние
функции Р(х) состоит в создании "гребня с крутыми
краями" вдоль каждой границы области ограничений. Следовательно,
если поиск начинается из допустимой точки и осуществляется поиск
минимума функции 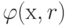 без ограничений, то минимум,
конечно, будет достигаться внутри допустимой
области для задачи с
ограничениями. Полагая r достаточно малой величиной,
для того чтобы влияние Р(х) было малым в точке минимума,
мы можем сделать точку минимума функции
без ограничений, то минимум,
конечно, будет достигаться внутри допустимой
области для задачи с
ограничениями. Полагая r достаточно малой величиной,
для того чтобы влияние Р(х) было малым в точке минимума,
мы можем сделать точку минимума функции 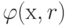 без
ограничений совпадающей с точкой минимума функции f(х)
с ограничениями.
без
ограничений совпадающей с точкой минимума функции f(х)
с ограничениями.
В общем случае невозможно аналитически определить положение
минимума функции 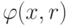 , рассматривая ее как
обычную функцию от r. Для его определения необходимо
обратиться к численным методам.
, рассматривая ее как
обычную функцию от r. Для его определения необходимо
обратиться к численным методам.
Следует отметить, что если целевая
функция f(х)
выпукла, а функция сj(х) вогнута, то
функция 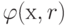 , заданная уравнением (1.4),
также является выпуклой функцией в области ограничений, которая
сама является выпуклой. Следовательно,
, заданная уравнением (1.4),
также является выпуклой функцией в области ограничений, которая
сама является выпуклой. Следовательно, 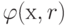 имеет для данного значения r единственный минимум.
имеет для данного значения r единственный минимум.
Если x1 и x2 -
точки, принадлежащие допустимой
области, т.е. 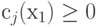 и
и 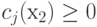 для j = 1,2,...,m, то при
для j = 1,2,...,m, то при  справедливо неравенство
справедливо неравенство
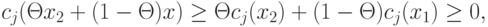
Таким образом, точка 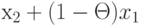 при
при  также является допустимой.
Кроме того, функция 1/сj(х) является
выпуклой для всех x, которые удовлетворяют
неравенству
также является допустимой.
Кроме того, функция 1/сj(х) является
выпуклой для всех x, которые удовлетворяют
неравенству 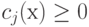 . Если h(х) = 1/сj(х), то
. Если h(х) = 1/сj(х), то
![\nabla h (x) = \frac{-\nabla c_j (x)}{[c_j(x)]^2} .](/sites/default/files/tex_cache/37fe1196dcd9d90e0da6513c512aaef9.png)
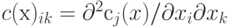 есть гессиан функции сj(х). Тогда, если p - произвольный вектор, то справедливо равенство
есть гессиан функции сj(х). Тогда, если p - произвольный вектор, то справедливо равенство![p^T \mathbf{H} (x) p =
-\frac{p^T C(x)p}{[c_j (x)]^2} +
\frac{2[p^T \nabla c_j (x)]^2}{[c_j (x)]^3} ,](/sites/default/files/tex_cache/aee2a52d17b2e494a8bb6e6edc7ce4e5.png)
где всегда рTН(х)р > 0, так как С(х) - отрицательно определенная матрица ввиду того,
что сj(х) - выпуклая функция и 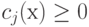 . Тогда матрица Н(х)
положительно определена и 1/сj(х) выпукла
во вcей области. Eсли r > 0, то функция Р(х), заданная уравнением (1.3), и функция
. Тогда матрица Н(х)
положительно определена и 1/сj(х) выпукла
во вcей области. Eсли r > 0, то функция Р(х), заданная уравнением (1.3), и функция 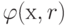 , заданная уравнением (1.4), также выпуклы.
, заданная уравнением (1.4), также выпуклы.
Предположим, что 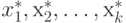 -
минимальные точки функции
-
минимальные точки функции 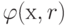 для убывающей
последовательности значений r1, r2, ..., rk, ...,
стремящейся к нулю. Тогда последовательность точек
для убывающей
последовательности значений r1, r2, ..., rk, ...,
стремящейся к нулю. Тогда последовательность точек 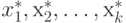 , сходится к оптимальному
решению задачи с ограничениями (см. уравнения (1.1) и (1.2)) при
, сходится к оптимальному
решению задачи с ограничениями (см. уравнения (1.1) и (1.2)) при 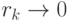 . Следовательно,
. Следовательно,
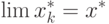 |
( 1.5) |
![\lim_{r_k \rightarrow 0} [\min \varphi (x, r_k)] = f(x^*)](/sites/default/files/tex_cache/cc3a49f163b72e2cf4922dc88f4e77f2.png) |
( 1.6) |
Полученный результат можно доказать следующим образом.
Поскольку f(х) непрерывная функция и 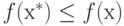 для всех допустимых точек,
то, задав произвольное достаточно малое значение
для всех допустимых точек,
то, задав произвольное достаточно малое значение 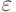 , можно найти допустимую точку х', такую, что
, можно найти допустимую точку х', такую, что
 |
( 1.7) |
Поскольку rk - убывающая
последовательность, стремящаяся к нулю, можно найти
такое значение K, что для  справедливо неравенство
справедливо неравенство
![r_k \leqslant
\left\{ \frac{\varepsilon}{2m} \min_j
\left[ \frac{1}{c_j (x')}
\right] \right\}.](/sites/default/files/tex_cache/75877a3892442c4188434b50b3bcaf6d.png) |
( 1.8) |
Поскольку P(x) > 0 из определения функции 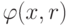 , имеем
, имеем
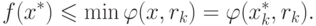 |
( 1.9) |
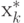 - минимальная точка функции
- минимальная точка функции 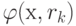 для задачи без ограничений. Кроме
того, если k > К, то rk < rK и справедливо
неравенство
для задачи без ограничений. Кроме
того, если k > К, то rk < rK и справедливо
неравенство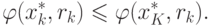 |
( 1.10) |
Это следует из того, что, поскольку 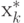 минимизирует функцию
минимизирует функцию 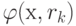 в любой
другой точке области x, в частности в точке
в любой
другой точке области x, в частности в точке 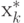 , функция будет принимать значение,
большее чем
, функция будет принимать значение,
большее чем 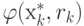 . Поэтому
. Поэтому
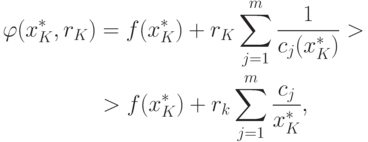
Следовательно,
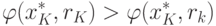
Тогда
 |
( 1.11) |
Но так как значение 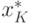 минимизирует функцию
минимизирует функцию 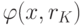 , то
, то
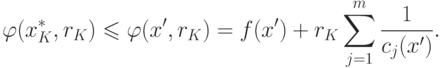 |
( 1.12) |
Следовательно, из уравнений (1.11) и (1.12) получим
 |
( 1.13) |
Из уравнения (1.8) следует, что
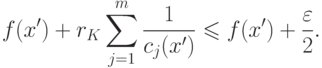 |
( 1.14) |
Тогда из уравнения (1.7) следует, что
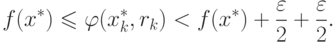
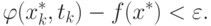 |
( 1.15) |
Поскольку 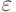 может быть выбрано произвольно
малым, всегда можно найти такое значение k, при котором
может быть выбрано произвольно
малым, всегда можно найти такое значение k, при котором
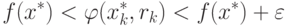
Таким образом, при 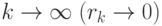
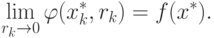 |
( 1.16) |
Из приведенного выше доказательства следует, что при 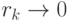
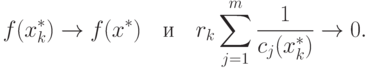 |
( 1.17) |
В качестве упражнения оставлено доказательство того, что 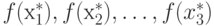 образуют
убывающую последовательность, такую, что
образуют
убывающую последовательность, такую, что
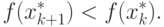 |
( 1.18) |
Очевидно, что если функция f(х) выпукла, а функция cj(х) при j = 1,...,n вогнута, то функция f(х) при наличии ограничении имеет единственный минимум.
