Введение в математическое программирование
[+]
Донецкий национальный технический университет
Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3134 / 727 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист
Теги: beta, анализ, базисное решение, вычисления, двойственная задача, задача линейного программирования, законы, искусственная жизнь, исследования, метод полного исключения, моделирование, нелинейное программирование, оптимальный план, поиск, программирование, симплекс, симплекс-метод, функция лагранжа, экстремум функции, электронная почта, элементы

Лекция 13: Решение задач нелинейного программирования с ограничениями. Геометрическая интерпретация задач нелинейного программирования

A
|
версия для печати
< Лекция 12 || Лекция 13: 1234

4. Геометрическая интерпретация задач нелинейного программирования

Задачи нелинейного программирования самого различного физического смысла допускают геометрическую интерпретацию. Рассмотрим такую интерпретацию для наиболее наглядного и простого случая двух переменных, \overline{X}=[x_1,x_2], \; E^n - плоскость.

Пример.

Найти вектор \overline{X}=[x_1,x_2], доставляющий минимум

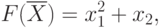F(\overline{X}) = x_1^2 + x_2 , ( 4.1)
при ограничениях
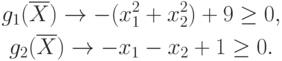
\begin{gathered} g_1(\overline{X}) \rightarrow -(x_1^2 + x_2^2) + 9 \ge 0, \\ g_2(\overline{X}) \rightarrow -x_1 - x_2 + 1 \ge 0. \end{gathered}

Строим область допустимых решений G. Для этого преобразуем ограничения.

Ограничение 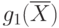g_1(\overline{X}) будет иметь вид:

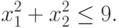
x_1^2 + x_2^2 \le 9.
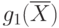Тогда ограничение g_1(\overline{X}) отсекает на плоскости круг радиусом r=3.

Ограничение 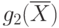g_2(\overline{X}) будет иметь вид:

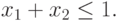
x_1 + x_2 \le 1 .
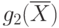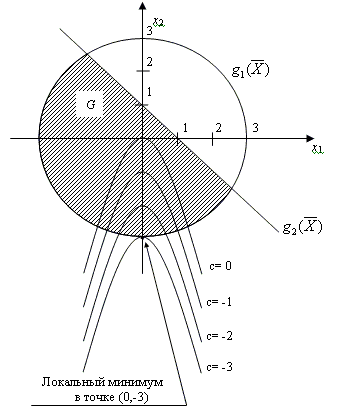
Тогда ограничение g_2(\overline{X}) отсекает на плоскости полуплоскость, ограниченную уравнением x1+x2=1.

В результате область допустимых решений G будет иметь вид, представленный на рис 13.2.

Строим линии уровня целевой функции (4.1). Линией уровня называется множество точек, с координатами [x1,x2] для которых целевая функция F(\overline{X}) имеет постоянное значение, т.е.

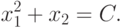
x_1^2 + x_2 = C .
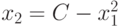Отсюда x_2 = C- x_1^2.

Меняя значения C, получим различные линии уровня.

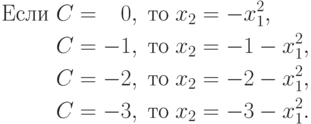
\begin{aligned} \text{Если } & C=\phantom{-}0, \; \text{то} \; x_2 = -x_1^2, \\ & C=-1, \; \text{то} \; x_2 = -1 -x_1^2, \\ & C=-2, \; \text{то} \; x_2 = -2 -x_1^2, \\ & C=-3, \; \text{то} \; x_2 = -3 -x_1^2. \end{aligned}

Как видно, линии уровня целевой функции (4.1) - это квадратичные параболы, симметричные относительно x2. Положение каждой параболы зависит от значения константы C (рис 13.2.). Исследуя полученные линии уровня получим что минимальное значение целевой функции (4.1) находится на границе области G, в точке с координатами [0,-3].


Рис. 13.2.
Дальше >>
< Лекция 12 || Лекция 13: 1234

Вопросы и ответы

вопросов: 0