Введение в математическое программирование
[+]
Донецкий национальный технический университет
Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3134 / 727 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист
Теги: beta, анализ, базисное решение, вычисления, двойственная задача, задача линейного программирования, законы, искусственная жизнь, исследования, метод полного исключения, моделирование, нелинейное программирование, оптимальный план, поиск, программирование, симплекс, симплекс-метод, функция лагранжа, экстремум функции, электронная почта, элементы

Лекция 12: Оптимизация при наличии ограничений. Ограничения в виде равенств. Ограничения в виде неравенств. Выпуклость и вогнутость. Комплексный метод

A
|
версия для печати
< Лекция 11 || Лекция 12: 1234 || Лекция 13 >
Аннотация: Данная лекция рассматривает оптимизацию при наличии различного рода ограничений, в частности, ограничений в виде равенств и неравенств; вводятся понятия выпуклости и вогнутости и определяется их роль в решении задач оптимизации; также рассматривается комплексный метод решения задач как модификация симплексного метода Нелдера – Мида, определяются его преимущества и недостатки.
Ключевые слова: функция Лагранжа, множители Лагранжа, ограничения в виде неравенств, математическое программирование, ограничения в виде равенств, условия Куна - Таккера, локальные минимумы, хорда, выпуклое множество, гессиан

1. Ограничения в виде равенств

Рассмотрим задачу минимизации функции двух переменных

z =f(x,y),

где на x и y наложено ограничение, задаваемое уравнением

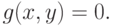g(x,y) =0. ( 1.1)

Вообще, уравнение g(x, у) = 0 можно разрешить относительно y как функцию от x т.е. у = h(x). Конечно, на практике может оказаться трудным или даже невозможным найти явный вид функции h(x). При выполнении определенных условий дифференцируемости производная функции h(x)

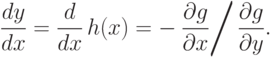\frac{dy}{dx} = \frac{d}{dx} \, h(x) = - \left. \frac{\partial g}{\partial x} \right/ \frac{\partial g}{\partial y} . ( 1.2)
Тогда функцию
z = f(x,y) = f[x,h(x)] ( 1.3)
можно записать как функцию одной независимой переменной x. Необходимым условием минимума функции z будет соотношение
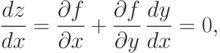
\frac{dz}{dx} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \, \frac{dy}{dx} = 0,
т.е.
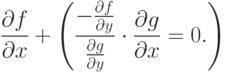\frac{\partial f}{\partial x} + \left( \frac{-\frac{\partial f}{\partial y}}{\frac{\partial g}{\partial y}} \cdot \frac{\partial g}{\partial x} = 0. \right) ( 4.1)

Соотношения (1.1) и (1.2) могут быть решены с целью получения значений х*, у* в точке минимума.

Этот результат может быть представлен в иной форме. Если положить

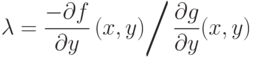\left. \lambda = \frac{-\partial f}{\partial y} \, (x,y) \right/ \frac{\partial g}{\partial y} (x,y) ( 1.5)
при х = х*, у = у*, то в точке минимума выполняются соотношения
\begin{aligned} & g(x,y) =0, \\ & \frac{\partial f}{\partial x}(x,y) +\lambda \frac{\partial g}{\partial x}(x,y) = 0, \\ & \frac{\partial f}{\partial y}(x,y) +\lambda \frac{\partial g}{\partial y}(x,y) = 0, \end{aligned}
причем последнее следует непосредственно из соотношения (1.5).

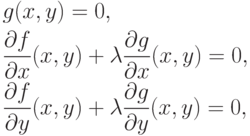
Получить эти три необходимых условия можно, используя функцию Лагранжа

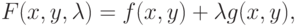F(x,y,\lambda) = f(x,y) + \lambda g(x,y), ( 1.6)
которая представляет собой сумму целевой функции и произведения множителя Лагранжа \lambda на функции ограничения. Тогда необходимые условия минимума функции f(x,у) при наличии ограничений могут быть записаны в следующем виде:
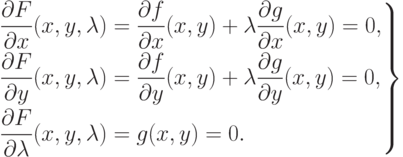\left. \begin{aligned} & \frac{\partial F}{\partial x}(x,y,\lambda) = \frac{\partial f}{\partial x}(x,y) + \lambda \frac{\partial g}{\partial x}(x,y) = 0 , \\ & \frac{\partial F}{\partial y}(x,y,\lambda) = \frac{\partial f}{\partial y}(x,y) + \lambda \frac{\partial g}{\partial y}(x,y) = 0 , \\ & \frac{\partial F}{\partial \lambda}(x,y,\lambda) = g(x,y) = 0. \end{aligned} \right\} ( 1.7)

Это система трех уравнений, решениями которой являются значения х*, у* и 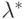\lambda^* - в точке минимума.

Необходимые условия минимума (1.7) могут быть обобщены для функций n переменных при наличии m ограничений в виде равенств. Рассмотрим задачу минимизации функции

z=f(x)=f(x1, x2, ..., xn),

где на переменную x наложены ограничения

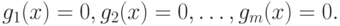g_1(x) = 0, g_2(x) = 0, \ldots, g_m(x) = 0. ( 1.8)

Ограничения можно использовать для того, чтобы выразить m переменных (без ограничения общности их можно обозначить x1, x2, ..., xm ) через остальные (n - m) переменных, которые можно рассматривать как независимые переменные. В точке минимума при наличии ограничений 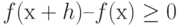f(х + h) – f(х) \ge 0 для всех h, удовлетворяющих условию gi(x+h)–gi(x)=0 при i = 1, ..., m.

Тогда c точностью до первого порядка hj будем иметь

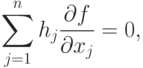
\sum_{j=1}^n h_j \frac{\partial f}{\partial x_j} = 0,
где
\sum_{j=1}^n h_j \frac{\partial g_i}{\partial x_j} = 0 \; \text{при } i=1,2,\ldots,m.

Это условие можно записать иначе:

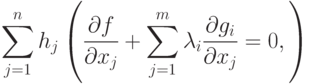\sum_{j=1}^n h_j \left( \frac{\partial f}{\partial x_j} + \sum_{j=1}^m \lambda_i \frac{\partial g_i}{\partial x_j} = 0, \right) ( 1.9)
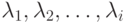где \lambda_1,\lambda_2,\ldots,\lambda_i - множители Лагранжа.

Поскольку hm+1,hm+2,...,hn являются независимыми приращениями, коэффициенты при них должны быть равны нулю, т.е.

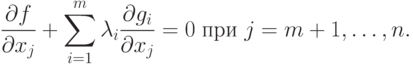
\frac{\partial f}{\partial x_j} + \sum_{i=1}^m \lambda_i \frac{\partial g_i}{\partial x_j} = 0 \; \text{при } j=m+1, \ldots, n.

Приращения h1,h2,...,hm не являются независимыми, и их можно положить равными нулю выбором множителей Лагранжа в уравнении (1.9). Таким образом, мы выбираем множители 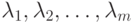\lambda_1,\lambda_2,\ldots,\lambda_m такими, чтобы

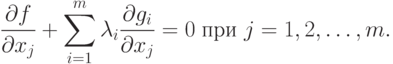
\frac{\partial f}{\partial x_j} + \sum_{i=1}^m \lambda_i \frac{\partial g_i}{\partial x_j} = 0 \; \text{при } j=1,2,\ldots,m.

Тогда окончательно будем иметь

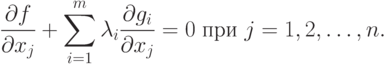\frac{\partial f}{\partial x_j} + \sum_{i=1}^m \lambda_i \frac{\partial g_i}{\partial x_j} = 0 \; \text{при } j=1,2,\ldots,n. ( 1.10)

Следовательно, если определить функцию Лагранжа в виде

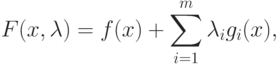F(x,\lambda)=f(x)+\sum_{i=1}^m \lambda_i g_i(x), ( 1.11)
то необходимые условия минимума функции f(х) при наличии ограничений можно записать следующим образом:
\frac{\partial F}{\partial x_j} = \frac{\partial f}{\partial x_j} + \sum_{i=1}^m \lambda_i \frac{\partial g_i}{\partial x_j} = 0 \; \text{при } j=1,2,\ldots,n. ( 1.12)
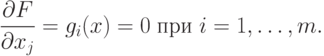\frac{\partial F}{\partial x_j} = g_i(x)=0 \;\text{при } i=1,\ldots,m. ( 1.13)

Отметим, что для допустимых значений x (таких, которые удовлетворяют ограничениям) справедливо соотношение

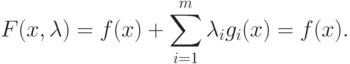
F(x,\lambda) = f(x) + \sum_{i=1}^m \lambda_i g_i (x) = f(x).

В точке минимума при наличии ограничений на значение х* можно записать, что f(х^* + h) - f(х^*) \ge 0, где h удовлетворяет уравнению gi(x*+h)=0 для всех i.

Таким образом,

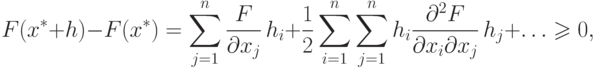
F(x^*+h)-F(x^*)=\sum_{j=1}^n \frac{ F}{\partial x_j} \, h_i + \frac12 \sum_{i=1}^n \sum_{j=1}^n h_i \frac{\partial^2 F}{\partial x_i \partial x_j} \,h_j + \ldots \geqslant 0,
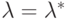где производные вычислены в точке х* при \lambda = \lambda^*. С учетом уравнения (1.12) получим для всех h, удовлетворяющих ограничениям, что
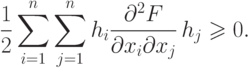
\frac12 \sum_{i=1}^n \sum_{j=1}^n h_i \frac{\partial^2 F}{\partial x_i \partial x_j} \,h_j \geqslant 0.

Достаточными условиями минимума при наличии ограничений являются уравнения (1.12) и (1.13), а также положительная определенность квадратичной формы

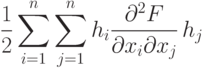\frac12 \sum_{i=1}^n \sum_{j=1}^n h_i \frac{\partial^2 F}{\partial x_i \partial x_j} \,h_j ( 1.14)
для значений h, удовлетворяющих ограничениям.

Замечание. Не всегда просто привести квадратичную форму к виду пригодному для использования.

Дальше >>
< Лекция 11 || Лекция 12: 1234 || Лекция 13 >

Вопросы и ответы

вопросов: 0