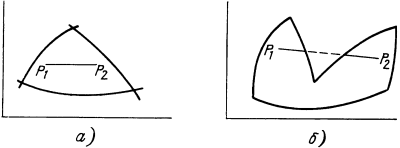Лекция 12: Оптимизация при наличии ограничений. Ограничения в виде равенств. Ограничения в виде неравенств. Выпуклость и вогнутость. Комплексный метод
3. Выпуклость и вогнутость
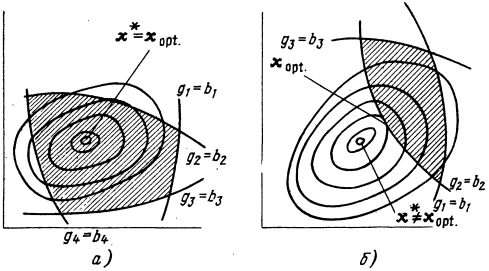
Общая задача математического программирования является очень сложной и до cих пор не имеет полного решения. Некоторые трудности встречаются в задачах, графически проиллюстрированных (рис. 12.1). На рисунке изображены линии постоянного уровня функции. По мере перемещения от точки х* - точки минимума функции при отсутствии ограничений - значения функции будут расти. На рис. 12.1 показаны также границы области ограничений gi(x) = bi, а сама область заштрихована.
На рис. 12.1,a минимум
функции при наличии ограничений совпадает с минимумом функции
без ограничений. Все ограничения имеют вид строгих неравенств,
и, зная это, можно было бы пренебречь ограничениями и решить
зaдачу методами, изложенными в изложенными ранее.
На рис. 12.1,б точка
минимума при наличии ограничений лежит на кривой g2(x) = b2, а два других
ограничения неактивны. Зная это, можно было бы пренебречь
ограничениями g1 и g3 и решить эту задачу как задачу с
ограничениями в виде равенств, учитывая только ограничение g2(х) = b2. Из этого следует,
что в точке минимума x при наличии ограничений
справедливо соотношение 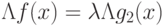 , поскольку
направление
, поскольку
направление 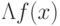 перпендикулярно линии
постоянного уровня и границе области ограничений в данной
точке. (Сравните с уравнением (2.3).)
перпендикулярно линии
постоянного уровня и границе области ограничений в данной
точке. (Сравните с уравнением (2.3).)
Возможно, что наличие ограничений будет приводить к появлению локального минимума. Это может произойти даже в том случае, когда функция имеет только одну точку минимума при отсутствии ограничений. Такая ситуация иллюстрируется рис. 12.2
Функция имеет только одну точку минимума при отсутствии ограничений. Однако для задачи с ограничениями обе точки A и B являются локальными минимумами, поскольку ни в одной из допустимых точек в ближайших окрестностях A или B функция не принимает меньших значений.
Некоторые из рассмотренных трудностей устраняются, если ограничиться случаем, когда область ограничений выпукла, а минимизируемая (максимизируемая) функция выпукла (вогнута).
Определим эти термины. Область является выпуклой, если отрезок
прямой, соединяющей любые две точки области, принадлежит этой
области. Следовательно, если x1 и x2 находятся в этой области, то любая
точка вида 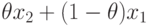 , где
, где  , находится в этой же области.
На рис. 12.3,а изображена
выпуклая область, а на рис. 12.3,б
- невыпуклая.
, находится в этой же области.
На рис. 12.3,а изображена
выпуклая область, а на рис. 12.3,б
- невыпуклая.
Функция f(х) является выпуклой на выпуклой области X, если для любых двух точек 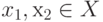 выполняется соотношение
выполняется соотношение
![f[\theta x_2 + (1-\theta)x_1] \leqslant \theta f(x_2)+(1-\theta)f(x_1)
\quad \text{при} \quad 0 < \theta < 1.](/sites/default/files/tex_cache/441da633e443a0f7d2f24e9914a6bf20.png) |
( 3.1) |
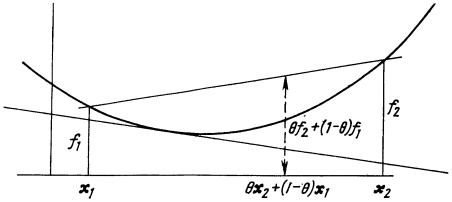
Для функции одной переменной это означает, что она лежит ниже хорды, соединяющей любые две точки ее графика (рис. 12.4).
Для вогнутой функции, определенной на выпуклом множестве, следует изменить знак неравенства, в результате чего получим соотношение
![f[\theta x_2 + (1-\theta)x_1] \geqslant \theta f(x_2)+(1-\theta)f(x_1).](/sites/default/files/tex_cache/9f244503a9c847f8cd7f36f9030b1816.png) |
( 3.2) |
Такая функция лежит выше хорды, соединяющей любые две точки ее графика.
Если в соотношениях (3.1) и (3.2) неравенства заменить на строгие неравенства, то функция f(х) будет строго выпуклой или строго вогнутой.
Есть еще два важных свойства выпуклых (вогнутых) функций,
которые можно вывести из соотношений (3.1) и (3.2). Если
функция f(х) выпукла на выпуклой области X и 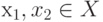 то
то
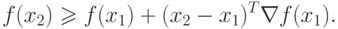 |
( 3.3) |
Для вогнутых функций знак неравенства меняется на противоположный,
что устанавливается следующим образом. Поскольку f(х)
выпукла, то для 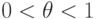 справедливо соотношение
справедливо соотношение
![f[\theta x_2 + (1-\theta)x_1] \leqslant \thetaf(x_2) + (1-\theta)f(x_1)](/sites/default/files/tex_cache/e6ee6be0e79ba92d41bac5a4286c651c.png)
![f[x_1 + \theta(x_2 - x_1)] - f(x_1) \leqslant \theta [f(x_2) - f(x_1)]](/sites/default/files/tex_cache/57c40288a3711a37c745cb245b16e03e.png)
![f(x_2) \geqslant f(x_1) + \frac{f[x_1 + \theta(x_2 - x_1)]- f(x_1)}{\theta}.](/sites/default/files/tex_cache/c46436e4253ecbddd5c7cdbe4d7444fb.png)
Но по теореме о среднем
![f[x_1 + \theta(x_2 - x_1)] = f(x_1) + \theta(x_2 - x_1)^T \nabla f[x_1 + \lambda \theta (x_2 - x_1)],](/sites/default/files/tex_cache/c1f841e83c6a00806e8c6cba0585aa73.png)
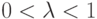 , т. е. производная
вычисляется в некоторой точке, лежащей между точками x1 и
, т. е. производная
вычисляется в некоторой точке, лежащей между точками x1 и 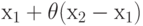 .
.Следовательно,
![f(x_2) \geqslant f(x_1) + (x_2 - x_1)^T \nabla f[x_1 \theta \lambda (x_2 - x_1)]](/sites/default/files/tex_cache/fb6b241fcd78df57fcbb1dbddbb90be3.png)
 получаем соотношение (3.3).
получаем соотношение (3.3).Из соотношения (3.3) следует, что выпуклые функции одной переменной (двух переменных) лежат выше любой касательной (плоскости) к данной функции (см. рис. 12.4).
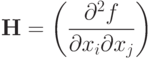
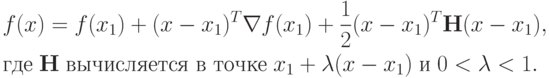
Таким образом, достаточно показать, что положительно определенная
квадратичная функция 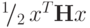 является выпуклой. Это сделать несложно.
является выпуклой. Это сделать несложно.
Пусть x1 и x2 -
произвольные значения x и пусть 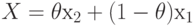 , где
, где 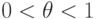 .
.
Тогда
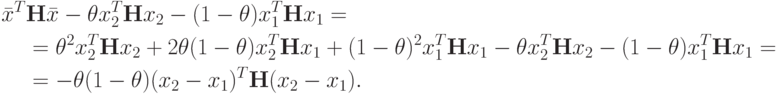
Так как 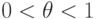 , то
, то 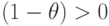 , и если матрица Н
положительно определена, то
, и если матрица Н
положительно определена, то  .
Следовательно,
.
Следовательно,
![[\theta x_2 + (1-\theta)x_1]^T \mathbf{H}
[\theta x_2 + (1-\theta)x_1] \leqslant
\theta x_2^T \mathbf{H} x_2 +
(1-\theta)x_1^T \mathbf{H} x_1 .](/sites/default/files/tex_cache/090ca98a5ed7c7fd4fa4894738bedb70.png) |
( 3.4) |
Для выпуклых функций одной переменной это означает, что вторая производная неотрицательна, поэтому первая производная является возрастающей функцией, которая может быть равна нулю только в одной точке. Следовательно, такая функция может иметь только одну точку минимума.