Лекция 6: Двойственный симплекс – метод. Исследование моделей задач линейного программирования на чувствительность
1. Двойственный симплекс – метод
Использование идей двойственности в сочетании с общей идеей симплекс-метода позволило разработать еще один метод решения задач ЛП - двойственный симплекс-метод. Впервые этот метод был предложен Лемке в 1954г. Решение задачи ЛП двойственным симплекс-методом сводится к отысканию оптимального плана прямой задачи последовательным переходом от одного базиса к другому.
Задача ЛП в канонической форме имеет вид:
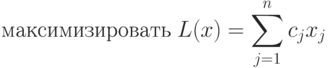 |
( 1.1) |
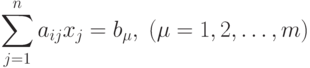 |
( 1.2) |
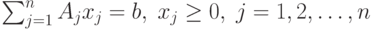 .
.Предположим, что  и ранг матрицы А
равен m.
и ранг матрицы А
равен m.
Двойственная задача к задаче (1.1), (1.2) записывается так:
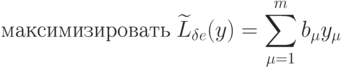 |
( 1.3) |
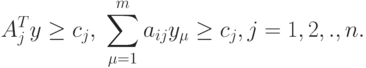 |
( 1.4) |
Назовем сопряженным базисом,
или базисом двойственной задачи такую систему из m
линейно-независимых векторов матрицы ограничений прямой задачи 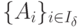 , для которой базисное решение y соответствующей системы линейных уравнений вида
, для которой базисное решение y соответствующей системы линейных уравнений вида
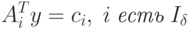 |
( 1.5) |
Разложим вектор b по сопряженному базису
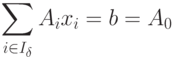 |
( 1.6) |
Решив систему (1.6), получим некоторое ее базисное решение  , которое называется псевдопланом прямой
задачи, так как для него может выполняться
условие неотрицательности переменных xi0.
, которое называется псевдопланом прямой
задачи, так как для него может выполняться
условие неотрицательности переменных xi0.
Таким образом, псевдоплан прямой задачи есть базисное решение относительно сопряженного базиса.
Как известно, оценки для небазисных векторов 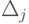 определяется в соответствии с
определяется в соответствии с
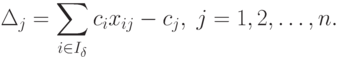 |
( 1.7) |
Псевдоплан можно найти и независимо от двойственной задачи.
Пусть 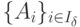 - произвольная
система линейно-независимых векторов прямой задачи.
- произвольная
система линейно-независимых векторов прямой задачи.
Выразим все небазисные векторы {Aj} через базисные:
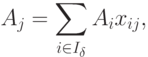 |
( 1.8) |
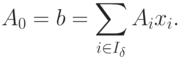 |
( 1.9) |
Обозначим решение (1.9) через х0.
Тогда можно дать дополнительное определение псевдоплана: n - мерный вектор X, для которого xi = xi0 при 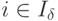 , и xj=0 при
, и xj=0 при 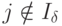 , является псевдопланом тогда и только тогда, когда все
, является псевдопланом тогда и только тогда, когда все 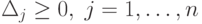 .
.
Доказательство. Векторы 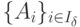 , линейно независимы.
, линейно независимы.
Поэтому можно вычислить такой y={y1,y2,...,ym}, для которого
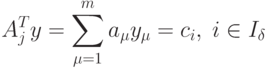 |
( 1.10) |
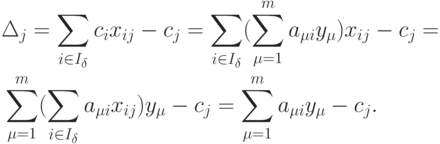
С учетом (1.4) получим
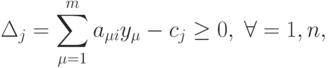 |
( 1.11) |
Рассмотрим некоторый сопряженный базис и соответствующий ему псевдоплан.
Справедлив следующий признак оптимальности: если среди базисных компонентов псевдоплана Х нет отрицательных, то псевдоплан Х={xi0} оказывается оптимальным решением прямой задачи.
Доказательство. Имеет место такая цепочка равенств:
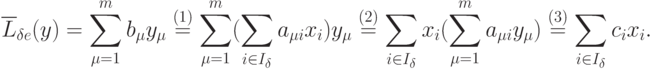
Равенство (1) следует из (1.2), равенство (2) получено переменой порядка суммирования, равенство (3) следует из (1.10).
Так как
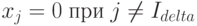 |
( 1.12) |
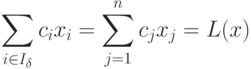 |
( 1.13) |
Таким образом, 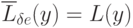 ,
что и является признаком оптимальности планов х и у,
если
,
что и является признаком оптимальности планов х и у,
если  .
.
Этот признак является необходимым и достаточным условием оптимальности в случае невыродженности базисного решения y двойственной задачи .
Пусть известен некоторый сопряженный базис 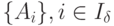 , которому
соответствует псевдоплан х.
Очевидно,
, которому
соответствует псевдоплан х.
Очевидно, 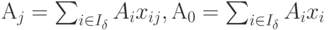 .
При этом в зависимости от знаков {xi} и {xij}
может иметь место один из трех случаев:
.
При этом в зависимости от знаков {xi} и {xij}
может иметь место один из трех случаев:
- базисные компоненты
 для всех
для всех 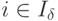 ;
; - среди хi имеются отрицательные, причем
для некоторого i: хi0<0, а все
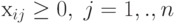 ;
; - псевдоплан содержит отрицательные компоненты хi0<0, но для каждой из них среди элементов {хij}, j=1,...,n, имеются отрицательные. В первом случае, как следует из достаточного признака оптимальности, псевдоплан х - оптимальное решение. Во втором случае задача не разрешима. В третьем случае можно перейти к некоторому новому сопряженному базису и, следовательно, к новому псевдоплану с меньшим значением L.
