НОУ ИНТУИТ | Введение в математическое программирование. Лекция 12: Оптимизация при наличии ограничений. Ограничения в виде равенств. Ограничения в виде неравенств. Выпуклость и вогнутость. Комплексный метод

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Донецкий национальный технический университет

Опубликован: 09.07.2007 | Доступ: свободный | Студентов: 3136 / 728 | Оценка: 4.34 / 4.12 | Длительность: 13:54:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист

|

Вам нравится? Нравится 52 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

2. Ограничения в виде неравенств

В этом разделе метод множителей Лагранжа будет распространен на ограничения в виде неравенств.

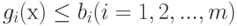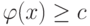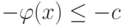Рассмотрим общую задачу математического программирования: минимизировать функцию f(х) при наличии m ограничений $g_i(х) \le b_i (i = 1, 2,..., m)$ , Причем такие ограничения не ограничивают общности. (Ограничение $\varphi(x) \ge c$ можно записать в виде $-\varphi(x) \le -c$ .

В настоящее время нет метода, гарантирующего существование решения любой подобной задачи.

Ограничения в виде неравенств могут быть преобразованы в ограничения в виде равенств добавления к каждому из них неотрицательной ослабляющей переменной 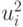u_i^2 (отметим, что переменная 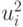u_i^2 всегда положительна):

или

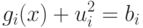
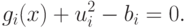( 2.1)

Таким образом, задача сводится к минимизации функции f(х) при наличии m ограничений в виде равенства 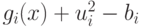g_i(x) + u_i^2 - b_i . Следуя изложенному в предыдущем разделе методу, сформируем функцию Лагранжа

$F(x,\lambda,u)=f(x)+\sum_{i=1}^m \lambda_i[g_i(x)+u_i^2-b_i].$

( 2.2)

Необходимыми условиями, которые должны выполняться в стационарной точке, являются следующие:

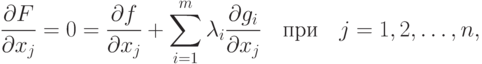$\frac{\partial F}{\partial x_j} = 0 = \frac{\partial f}{\partial x_j} + \sum_{i=1}^m \lambda_i \frac{\partial g_i}{\partial x_j} \quad \text{при} \quad j=1,2,\ldots,n,$

( 2.3)

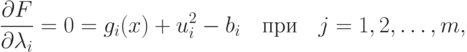$\frac{\partial F}{\partial \lambda_i} = 0 = g_i(x) + u_i^2 - b_i \quad \text{при} \quad j=1,2,\ldots,m,$

( 2.4)

$\frac{\partial F}{\partial u_i} = 0 = 2 \lambda_i u_i \quad \text{при} \quad j=1,2,\ldots,m,$

( 2.5)

Умножив последнее уравнение на u_i/2, получим

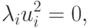
$\lambda_i u_i^2 = 0,$

т.е.

$\lambda_i [b_i - g_i(x)]=0 \quad \text{при} \quad j=1,2,\ldots,m.$

( 2.6)

Уравнения (2.3), (2.4) и (2.6) являются необходимыми условиями минимума в точке х* при наличии ограничений. Уравнения (2.4) являются повторной записью ограничений $g_i(x) \le 0$ . Уравнение (2.6) означает, что либо $\lambda_i = 0$ , либо b_i–g_i(x*)=0. Если $\lambda_i \neq 0$ , то g_i(x*)=b_i и ограничение является активным и представляет собой ограничение в виде равенства. С другой стороны, если ограничение является ограничением в виде строгого неравенства g_i(х*) < b_i, то соответствующий множитель Лагранжа $\lambda_i = 0$ . В самом деле, если g_i(x*) < b_i, то рассматривается минимум, удовлетворяющий ограничению, которое является неактивным, и которым можно пренебречь, а соответствующие множители $\lambda_i = 0$ . Конечно, предварительно не известно, какими ограничениями можно пренебречь.

Есть также дополнительное условие, которое должно быть выполнено в точке минимума при наличии ограничений, а именно 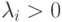$\lambda_i > 0$ .

Предположим, что уравнения (2.3), (2.4) и (2.6) справедливы в точке 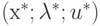$(х^*; \lambda^*; u^*)$ . Если фактический минимум функции при наличии ограничений z = f(х*), то можно рассматривать z как функцию от b_i и изменения b_i будут изменять ограничения и, таким образом, изменять саму функцию z. Покажем, что

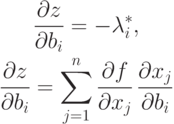$\begin{gathered} \frac{\partial z}{\partial b_i} = -\lambda_i^*, \\ \frac{\partial z}{\partial b_i} = \sum_{j=1}^n \frac{\partial f}{\partial x_j} \, \frac{\partial x_j}{\partial b_i} \end{gathered}$

( 2.7)

где частные производные вычисляются в точке х*.

Поскольку 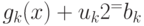g_k(x) + u_k2^ = b_k , то

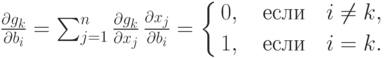
$\frac{\partial g_k}{\partial b_i} = \sum_{j=1}^n \frac{\partial g_k}{\partial x_j} \, \frac{\partial x_j}{\partial b_i} = \left\{ \begin{aligned} & 0,\quad \text{если} \quad i \neq k, \\ & 1,\quad \text{если} \quad i = k. \end{aligned} \right.$

Тогда

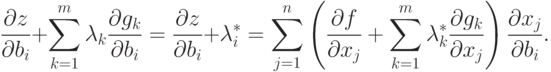
$\frac{\partial z}{\partial b_i} + \sum_{k=1}^m \lambda_k \frac{\partial g_k}{\partial b_i} = \frac{\partial z}{\partial b_i} + \lambda_i^* = \sum_{j=1}^n \left( \frac{\partial f}{\partial x_j} + \sum_{k=1}^m \lambda_k^* \frac{\partial g_k}{\partial x_j} \right) \frac{\partial x_j}{\partial b_i}.$

Но это выражение равно нулю в соответствии с уравнением (2.3). Таким образом,

$\frac{\partial z}{\partial b_i} = -\lambda_i^*.$

С возрастанием b_i область ограничений расширяется, что не может привести к увеличению значения z - минимума функции f(х), находящегося внутри области ограничений, а может лишь уменьшить его. Таким образом,

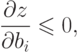
$\frac{\partial z}{\partial b_i} \leqslant 0,$

т.е.

$\lambda_i^* \geqslant 0.$

( 2.8)

Необходимые условия минимума функции f(х) при наличии ограничений g_i(х) < b_i (i=1,2,...,m) имеют такой вид, что можно найти x и 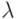$\lambda$ , для которых

$\left. \begin{aligned} \frac{\partial f}{\partial x_j} + \sum_{i=1}^m \lambda_i \frac{\partial g_i}{\partial x_j} = 0 \quad \text{при} \quad j=1,\ldots,n , \\ g_i(x) \leqslant b_i \quad \text{при} \quad i=1,2,\ldots,m; \\ \lambda_i [g_i(x)-b_i]=0 \quad \text{при} \quad i=1,2,\ldots,m, \\ \lambda_i \geqslant 0 \quad \text{при} \quad i=1,\ldots,m. \end{aligned} \right\}$

( 2.9)

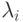(Знак $\lambda_i$ меняется на противоположный, если рассматривается максимум.)

Эти условия известны как условия Куна - Таккера.

Дальше >>

Авторизоваться

Введение в математическое программирование

Лекция 12: Оптимизация при наличии ограничений. Ограничения в виде равенств. Ограничения в виде неравенств. Выпуклость и вогнутость. Комплексный метод

2. Ограничения в виде неравенств

Вопросы и ответы