|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Потоки
Введем некоторые вспомогательные понятия и установим два полезных
соотношения. Пусть 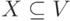 ,
,  .
Множество всех
ребер, у которых начальная вершина принадлежит
.
Множество всех
ребер, у которых начальная вершина принадлежит  , а концевая
-
, а концевая
-  ,
обозначим через
,
обозначим через  . Пропускной способностью
множества
. Пропускной способностью
множества  называется сумма пропускных способностей
всех
его ребер, она обозначается через
называется сумма пропускных способностей
всех
его ребер, она обозначается через 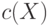 . Если
. Если  - поток, то для
каждого множества
- поток, то для
каждого множества 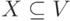 можно определить
величину
можно определить
величину 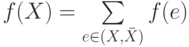 .
Очевидно, для любого множества
.
Очевидно, для любого множества  и любого потока
и любого потока  выполняется неравенство
выполняется неравенство 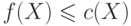 .
Множество
.
Множество  называется разрезом, если
называется разрезом, если 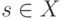 ,
, 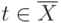 .
.
Лемма 1. Для любого потока  и любого разреза
и любого разреза  выполняется равенство
выполняется равенство 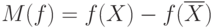 .
.
Доказательство. Рассмотрим величину 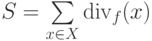 .
Так как дивергенция во внутренних вершинах равна нулю, то эта сумма
равна дивергенции источника, то есть величине потока
.
Так как дивергенция во внутренних вершинах равна нулю, то эта сумма
равна дивергенции источника, то есть величине потока 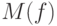 .
С другой
стороны, рассмотрим вклад, вносимый в эту сумму некоторым ребром
.
С другой
стороны, рассмотрим вклад, вносимый в эту сумму некоторым ребром 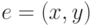 . Он зависит от того, в каком отношении к множеству
. Он зависит от того, в каком отношении к множеству  находится это ребро:
находится это ребро:
- если
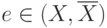 , то в сумму
, то в сумму  входит
слагаемое
входит
слагаемое 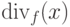 , которое, в свою очередь,
является суммой и содержит
слагаемое
, которое, в свою очередь,
является суммой и содержит
слагаемое  со знаком плюс; это единственное в данном случае
вхождение
со знаком плюс; это единственное в данном случае
вхождение  в
в  , так что вклад ребра
, так что вклад ребра  равен
равен  ;
; - если
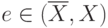 , то в
, то в  входит слагаемое
входит слагаемое 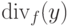 ,
которое, в свою очередь, содержит слагаемое
,
которое, в свою очередь, содержит слагаемое  со знаком
минус; вклад ребра
со знаком
минус; вклад ребра  в этом случае равен
в этом случае равен  ;
; - если ребро соединяет две вершины из
 , то
в сумме
, то
в сумме  присутствуют оба слагаемых
присутствуют оба слагаемых  и
и  и
суммарный вклад такого
ребра равен нулю;
и
суммарный вклад такого
ребра равен нулю; - ребро, соединяющее две вершины из
 , в сумме
, в сумме  вообще
не представлено.
вообще
не представлено.
Отсюда следует, что 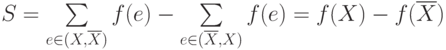 .
.
Лемма 2. Для любого потока  и любого
разреза
и любого
разреза  имеет место неравенство
имеет место неравенство 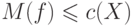 .
.
Доказательство. Это следует из леммы 1 и неравенств 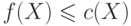 ,
, 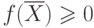 .
.
