| Россия, Сургут |
Алгоритм Шора
Мы собираемся пояснить этот метод на примере. Пусть N = 989 и это число следует факторизовать. Мы хотим найти порядок m для g = 2 в мультипликативной группе  , используя алгоритм Шора. Так как
, используя алгоритм Шора. Так как  , то
, то 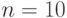 . После Шага 2 алгоритма Шора получим кубит:
. После Шага 2 алгоритма Шора получим кубит:
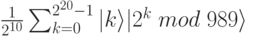
На Шаге 3 измерим значение последних 10 битов с наблюдаемым случайным значением. Предположим, что результат этого измерения 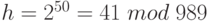 . Тогда только слагаемые, где
. Тогда только слагаемые, где 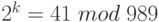 выживут в результирующей сумме. Эти значения k формируют арифметическую прогрессию k = 50, 50 + m, 50 + 2m, .... Следовательно, последовательность коэффициентов в кубите теперь периодическая с периодом m. Применяя КПФ -квантовое преобразование Фурье на Шаге 5, получим состояние:
выживут в результирующей сумме. Эти значения k формируют арифметическую прогрессию k = 50, 50 + m, 50 + 2m, .... Следовательно, последовательность коэффициентов в кубите теперь периодическая с периодом m. Применяя КПФ -квантовое преобразование Фурье на Шаге 5, получим состояние:
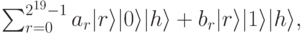
Коэффициенты Фурье имеют инки в точках r, близких к целым кратным 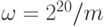 . Для иллюстрации построим график вероятностей ау + Ь для r в пределах от 0 до 40000. Мы понимаем, что значения коэффициентов
. Для иллюстрации построим график вероятностей ау + Ь для r в пределах от 0 до 40000. Мы понимаем, что значения коэффициентов
кубита, хранимые в квантовом компьютере, недоступны непосредственно, и мы смогли построить этот график только лишь потому, что значение N мало и для него возможно вычислить коэффициенты Фурье на обычном компьютере. Этот графин показывает вероятности наблюдения каждого значения r, если бы мы проводили измерения первых 19 кубитов. Мы четко различаем пики на графине, которые означают, что некоторые значения r намного чаще появляются при измерениях, чем другие.
Приведем список вероятностей наблюдения значений r вблизи двух пиков:

|
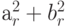 |
|---|---|
|
251926 251927 251928 251929 251930 251931 251932 251933 251934 |
0.0000071 0.0000124 0.0000271 0.0000991 0.0125868 0.0001465 0.0000329 0.0000141 0.0000078 |
 |
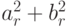 |
|---|---|
| 435767 435768 435769 435770 435771 435772 435773 435774 435775 |
0.000054 0.000091 0.000186 0.000567 0.008652 0.002382 0.000373 0.000145 0.000076 |
Из этих таблиц видно, что некоторые значения r имеют намного большую вероятность наблюдения. Предположим мы выполнили квантовый алгоритм дважды и получили r = 435771 в качестве первого наблюдения, и r = 251930 как результат выполнения при втором запуске квантового алгоритма. Мы ожидаем, что эти значения близки к кратным частоты 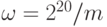 .
.
Давайте выполним алгоритм Эвклида для поиска наибольшего общего множителя 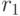 и
и 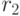 . Разделим
. Разделим 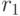 на
на 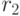 с остатком:
с остатком:
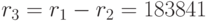
Этот остаток 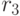 всегда меньше делителя
всегда меньше делителя 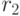 , но мы не ожидаем, что он на порядки меньше значения делителя. В самом деле, для 0 < с < 1 вероятность того, что
, но мы не ожидаем, что он на порядки меньше значения делителя. В самом деле, для 0 < с < 1 вероятность того, что  равна с.
равна с.
Давайте продолжим выполнять алгоритм Эвклида:
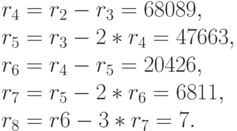
На последнем шаге мы замечаем, что значение остатка 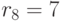 на несколько порядков меньше значения делителя
на несколько порядков меньше значения делителя  . Это и является признаком, когда алгоритм следует заканчивать, поскольку
. Это и является признаком, когда алгоритм следует заканчивать, поскольку  . Следовательно,
. Следовательно, 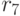 является приближенным
является приближенным 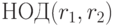 . Давайте определим соответствующие целые кратные:
. Давайте определим соответствующие целые кратные:
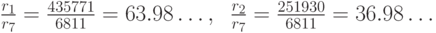
Теперь можно получить более точное значение базовой частоты  :
:

Из соотношения 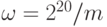 определим значение порядка m для элемента g = 2 в группе
определим значение порядка m для элемента g = 2 в группе  :
:
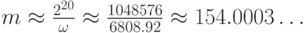
Мы заключаем, что элемент группы g = 2 имеет порядок m = 154.
По теореме Лагранжа размер М = (р - 1) (q - 1) группы  является целым, кратным порядку любого элемента, М = mК. Так как величина М сравнима с N = рq = 989, то можно аппроксимировать значение неизвестного множителя К как:
является целым, кратным порядку любого элемента, М = mК. Так как величина М сравнима с N = рq = 989, то можно аппроксимировать значение неизвестного множителя К как:

Взяв К = 6, получим значение М = 6m = 924.
Так как N = рq, М = (р - 1) (q - 1) = pq - р - q + 1, то имеем:
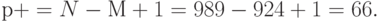
В итоге неизвестные множители р и q находятся как корни квадратного уравнения с известными коэффициентами:
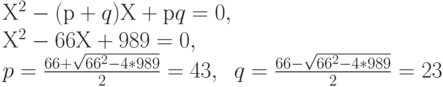
Можно проверить справедливость результатов факторизации:
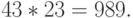
Упражнение. Покажите, что в нашем описании алгоритма Шора шаг 3 может быть опущен.