| Россия, Сургут |
Дискретное преобразование Фурье
Применяя формулу для  , получим:
, получим:

Используя второе тождество утверждения, упростим суммы:
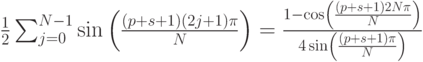
Так как синус в знаменателе не равен нулю, а числитель обращается в нуль, то сумма исчезнет. Вычисляя вторую сумму, получим:

Если 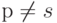 , то сумма равна нулю, но и когда р = s, то сумма также равна нулю, поскольку каждое слагаемое суммы становится равным нулю.
, то сумма равна нулю, но и когда р = s, то сумма также равна нулю, поскольку каждое слагаемое суммы становится равным нулю.
Мы заключаем, что 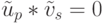 для всех р, s. Вычисление
для всех р, s. Вычисление  остается в качестве упражнения.
остается в качестве упражнения.
Обобщая, имеем:

Это завершает доказательство теоремы.
Для превращения базиса в ортонормальный базис, разделим каждый вектор на его длину:
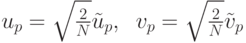
Так как  -базис в
-базис в 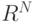 , то любой вектор
, то любой вектор  можно представить в этом базисе:
можно представить в этом базисе:
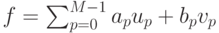
Коэффициенты 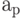 и
и 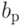 в этом выражении называются коэффициентами Фурье вектора f. Дискретное преобразование Фурье (ДПФ) - это преобразование вектора измерений в вектор коэффициентов:
в этом выражении называются коэффициентами Фурье вектора f. Дискретное преобразование Фурье (ДПФ) - это преобразование вектора измерений в вектор коэффициентов:

Изначальный вектор измерений описывает эволюцию сигнала во времени. Каждый коэффициент Фурье соответствует некоторой частоте. Говорят, что ДПФ - это преобразование сигнала из временной области в частотную область.
Нам необходимо решить задачу представления заданного вектора f в виде линейной комбинации векторов 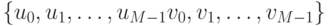 . Оказывается, что задача намного проще решается, когда базис векторов является ортонормальным.
. Оказывается, что задача намного проще решается, когда базис векторов является ортонормальным.
Утверждение. Пусть  -ортонормальный базис в
-ортонормальный базис в 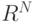 , пусть f - вектор в
, пусть f - вектор в 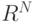 . Тогда коэффициенты разложения f в линейную комбинацию векторов базиса:
. Тогда коэффициенты разложения f в линейную комбинацию векторов базиса:

могут быть найдены как скалярное произведение:

Доказательство. Рассмотрим скалярное произведение обеих сторон линейной комбинации и вектора т:
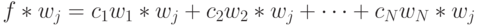
Так как базис ортонормальный, то все скалярные произведения в правой части окажутся равными нулю, за исключением произведения  , которое равно 1. Отсюда следует справедливость утверждения
, которое равно 1. Отсюда следует справедливость утверждения  .
.
Из утверждения непосредственно следуют формулы для вычисления коэффициентов Фурье:

Индекс р пробегает значения р = 0,1, ... , М - 1.
Если нам известны коэффициенты Фурье, то можно восстановить исходный сигнал  . Эта процедура называется обратным преобразованием Фурье.
. Эта процедура называется обратным преобразованием Фурье.
Так как

то можно вычислить 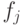 , взявj-ю компоненту каждого вектора:
, взявj-ю компоненту каждого вектора:

Как прямое, так и обратное преобразование Фурье являются линейными трансформациями 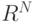 . При обратном ДПФ вектор (1,0,0, .. . , 0), соответствующий
. При обратном ДПФ вектор (1,0,0, .. . , 0), соответствующий  переходит в вектор
переходит в вектор  . Аналогично, образы стандартных базисных векторов
. Аналогично, образы стандартных базисных векторов 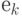 , являются векторами
, являются векторами  . Так как эти вектора ортонормальны, то мы заключаем, что обратное ДПФ является ортогональной линейной трансформацией. Инверсия ортогональной линейной трансформации - ортогональна. Из этого следует, что прямое ДПФ представляет ортогональную линейную трансформацию.
. Так как эти вектора ортонормальны, то мы заключаем, что обратное ДПФ является ортогональной линейной трансформацией. Инверсия ортогональной линейной трансформации - ортогональна. Из этого следует, что прямое ДПФ представляет ортогональную линейную трансформацию.
Это хорошая для нас новость, поскольку это означает, что ДПФ совместимо с парадигмой квантовых вычислений. Квантовая версия ДПФ, которая называется квантовым преобразованием Фурье (КПФ) является основой алгоритма Шора. Мы представим КПФ в следующей лекции.
Величина коэффициента Фурье показывает, насколько сильно соответствующая частота представлена в сигнале. В частности, когда мы применяем преобразование Фурье к периодическому сигналу, появляются пики со значениями 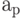 и
и  в точках р, соответствующих обертонам базовой частоты сигнала. Это именно то, что мы видели в спектре диаграммы ДПФ при записи звучания флейты.
в точках р, соответствующих обертонам базовой частоты сигнала. Это именно то, что мы видели в спектре диаграммы ДПФ при записи звучания флейты.
Давайте рассмотрим совсем простой пример периодического сигнала, который важен для алгоритма Шора. Зафиксируем два целых числа  и рассмотрим следующую последовательность длины N и периодом m:
и рассмотрим следующую последовательность длины N и периодом m:

Пусть N/m будет большим числом. Нетрудно видеть, что  для i =s + jm, где j = 0, 1, ... , L - 1. Здесь L - минимальное целое, большее или равное (N - s)/m.
для i =s + jm, где j = 0, 1, ... , L - 1. Здесь L - минимальное целое, большее или равное (N - s)/m.
Упражнение. Вычислим ДПФ для последовательности  Покажем, что коэффициенты Фурье даются следующими формулами:
Покажем, что коэффициенты Фурье даются следующими формулами:

Подсказка. Первое утверждение этой главы может быть полезным в этих вычислениях.
Давайте проанализируем, когда коэффициенты Фурье, полученные в этом упражнении, являются большими числами. Абсолютное значение числителей в этих формулах не может быть больше чем 2, поскольку значения синуса и косинуса не превосходят 1. Единственная возможность стать большим числом - иметь маленький знаменатель  . Это происходит, когда
. Это происходит, когда  близко к целом числу
близко к целом числу

Это эквивалентно тому, что

Мы видели, что пики в значениях коэффициентов Фурье расположены в точках р, кратных базовой частоте
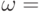
Смещением на 1/2 можно пренебречь. Заметьте, что положение пиков определяется периодом m и не зависит от s.
ДПФ широко используется в цифровой обработке сигналов, в частности для сжатия аудио файлов (стандарт МРЗ) и изображений (JРЕG). Давайте вкратце обсудим аудио сжатие.
Для звуковой волны большая часть измерений значений сигнала далеки от нулевых значений. Если выполнить ДПФ, то большинство коэффициентов Фурье будут близки к нулю, поскольку типичная звуковая волна находится в сравнительно узком диапазоне частот. Мы можем заменить малые коэффициенты Фурье нулями и хранить только существенные коэффициенты, значительно уменьшая объем данных. Это приводит к некоторому искажению записи, но с малой потерей качества достигается большой коэффициент сжатия.
