Аддитивные и мультипликативные группы остатков

Теперь мы можем доказать следующее:

Теорема. Остаток k имеет мультипликативный обратный элемент в , если и только если НОД(m, k) = 1.

Доказательство. Предположим, что НОД(m, k) = 1. По предыдущей теореме существуют целые u и v, такие что 1 = mu + kv. Так как mu = 0 тод т, то kv = 1 тод m, а это значит, что v является мультипликативным обращением k в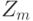

Для доказательства утверждения в другую сторону предположим, что v является мультипликативным обращением k в 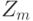. Тогда kv = 1 mod m. Два целых имеют одинаковые остатки по модулю m, если их разность делится на m. Так что kv - 1 = ms для некоторого s и kv-ms= 1. Если d -общий делитель k и m, то он также является делителем kv-ms, откуда следует, что d -делитель единицы и равен 1. Но тогда единственным общим делителем k и m является 1. Это и означает, что НОД(m, k) = 1.

Существует важный специальный случай, когда модулем является простое число р. Можно видеть, что в 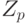каждый ненулевой остаток имеет мультипликативный обратный элемент, так что содержит р - 1 элемент.

Теорема (Малая теорема Ферма). Пусть р - простое число. Если а целое, не делящееся на р, то

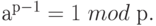
Доказательство. Применим теорему Лагранжа к мультипликативной группе 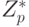. Так как порядок этой группы равен р -1, то для каждого элемента а в имеем 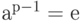, что в точности совпадает с утверждением теоремы.

Рассмотрим в качестве примера р = 13. Давайте определим порядок элемента g = 2 в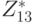

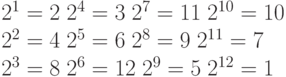
Следовательно, порядок элемента g = 2 в 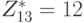, это также говорит нам, что 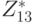- циклическая группа порядка 12 с генератором 2. Мы можем вычислить порядки всех элементов в 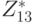. Так как 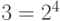, а 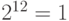, то порядок 3 равен З.

Определение. Изоморфизм двух групп - это взаимно-однозначное соответствие между элементами, сохраняющее групповые операции.

Функция 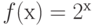является изоморфизмом между аддитивной группой 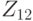и мультипликативной группой 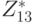. Она сохраняет групповые операции, так как .

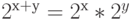Мы собираемся установить без доказательства следующий результат:

Теорема. Пусть р - простое число. Группа 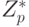имеет циклический генератор g, такой, что степени g исчерпывают 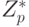. Функция f(х) =gх является изоморфизмом между 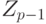и .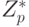

Не существует общего правила, указывающего какой элемент 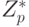является циклическим генератором. Более того, когда g задано, то функция 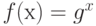является функцией ловушкой (trар-door function) в случае, когда р - большое простое число. Эту функцию просто вычислить, но трудно вычислить обращение f , которое дает остаток h в 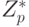, то есть трудно найти такое целое х, для которого 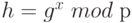. Так как f - экспоненциальная функция, то ее обращение представляет дискретно логарифмическую функцию: .

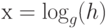Конечно, можно попытаться организовать полный перебор, но для больших простых чисел эта задача вычислительно невыполнима.

Существует несколько широко используемых криптосистем, основанных на предположении, что дискретная логарифмическая функция трудно вычислима.

В заключение этой лекции:

Теорема (Китайская теорема об остатках). Если НОД(m, s) = 1, то для любой пары остатков а mod m, b mod s существует уникальный остаток х mod ms, такой что х = а mod т и х = b mod s.

Пример. Система

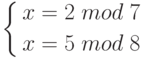
имеет единственное решение в 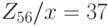(В данном примере: а = 2, b = 5, m = 7, s = 8, u = -1, v = 1. Откуда x =asv +bmu = 16-35 = -19 = 37 mod 56)

Доказательство. Так как НОД(m, s) = 1, то существуют u, v, такие что mu + sv = 1. Очевидно:

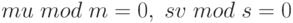
Тогда из равенства mu + з = 1 следует:

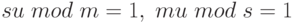
Сконструируем решение х следующего вида: х =asv +bmu mod ms. Проверим, что эта формула дает желаемый результат:

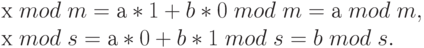
Так как число пар остатков (а mod m, b mod s) совпадает с числом остатков в , то решение будет единственным.

Следствие. Предположим НОД(m, s) = 1. Остаток k обратим в , если и только если k mod m обратим в 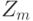и k mod s обратим в .

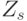Следствие. Предположим, что р, q - два простых числа и 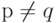. Тогда порядок группы 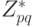равен (р - 1) (q - 1).

Применяя теорему Лагранжа, получаем аналог малой теоремы Ферма, которая используется в РSА криптосистеме:

Теорема. Предположим, что р, q - два простых числа и 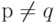. Если g не делится ни на р, ни на q, то: