Блеск и нищета квантовых компьютеров

Поляризованный свет используется в кинотеатрах 3D. Для создания 3D эффекта правый и левый глаз должны видеть слегка отличные картинки. Для этого фильм проецируется двумя камерами, разнесенными на некоторое расстояние. Изображение обеих камер одновременно проецируется на экран, но свет от двух проекторов поляризован различными способами. Очки для просмотра фильма имеют поляризационные фильтры, каждый из которых способен пропускать свет только от одного проектора. В результате два глаза получают различающиеся изображения, что и создает 3D эффект.

Вообразите, фотон с линейной поляризацией под углом а в плоскости ХУ Такой фотон может быть использован в качестве физической реализации кубита со значением

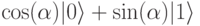
Небольшое техническое замечание относительно положительного и отрицательного состояний фотона 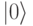и - 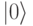. Оба состояния соответствуют фотону с теми же осями поляризации, однако осцилляция электрического поля для отрицательного состояния - 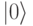находится в противофазе относительно состояния 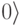. Для одного фотона невозможно различить, в каком состоянии он находится, но для пары фотонов можно обнаружить разницу в фазах и рассматривать их состояния как два различных значений кубита.

Давайте перейдем теперь к рассмотрению множества кубитов - мультикубитам. 2-кубит - это вектор с четырьмя компонентами в форме:

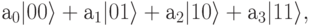
где 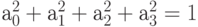. Базисные вектора в пространстве 2-кубитов: 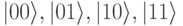, называемые также чистыми состояниями, соответствуют 4-м возможным состояниям пары классических битов. В общем случае значение 2-кубита представляет комбинацию значений 4-х классических битов. У каждого бита в этой комбинации есть свой весовой коэффициент. Эту комбинацию принято называть суперпозицией.

Например, 2-кубит 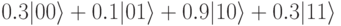представляет суперпозицию 4-х классических значений, но 2-бит значение "10" в этой комбинации наиболее весомо.

Как вы уже могли догадаться, 3-кубит - это вектор с 8-мю компонентами:

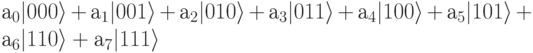
Обратите внимание на соответствие в нашей нотация между индексом коэффициента а и меткой, которой мы помечаем базисные вектора. Возьмем, например, терм (слагаемое) 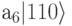. Значение 110 в этом терме совпадает с двоичной записью значения индекса .

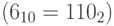Нетрудно также заметить, что число термов удваивается при увеличении на единицу числа кубитов. Для 1-кубита термов - 2, для 2-кубита - 4, для 3-кубита- 8. В общем случае для N кубитов термов 2^N. Для 8-кубита тeрмов будет 256:

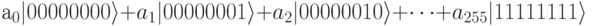
В качестве упражнения давайте определим индекс коэффициента "а" для терма с меткой . Каждая цифра в позиционной системе счисления является коэффициентом основания системы счисления в степени k,

где k - определяется позицией цифры. Для двоичной системы счисления основание равно 2, так что цифры 0 и 1- это коэффициенты при соответствующих степенях основания 2. Для 8-битного выражения самая левая цифра соответствует степени 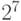, самая правая - 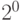. Бинарное выражение "11010011" следует рассматривать как:

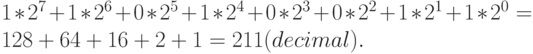
Аналогично, десятичный индекс 117 в двоичном 8-битном представлении имеет вид:

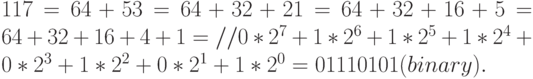
Для более компактной закиси мы иногда будем записывать 8-кубит в десятичной форме:

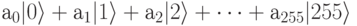
При этом мы понимаем, что все десятичные целые, появляющиеся в записи базисных векторов необходимо перевести в 8-битную двоичную форму записи.

При увеличении числа битов такие выражения становятся чрезмерно длинными. Эффективный математический способ записи таких сумм использует нотацию. При использовании этой нотации 8-кубит компактно записывается в виде:

Здесь k - индекс суммирования пробегает все значения от 0 до 255, так что сумма включает все 255 термов. При k=0 в сумму включается терм 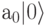при в сумму включается терм 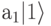и так далее. Для каждого базисного вектора 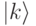целое следует переводить в двоичную форму записи.

Как мы увидим в следующей главе, состояние объединенной поляризации n взаимодействующих кубитов описывается как n-кубит. Объем памяти требуемой для записи такого состояния в классическом компьютере растет экспоненциально в зависимости от n. Если отводить 1 байт для записи значения каждого а-коэффициента, то нам потребуется 2 байта для хранения 1-кубита, один килобайт для хранения 10-кубит, один мегабайт для 20-кубитов, один гигабайт для 30-кубит, один терабайт для 40-кубит, один петабайт для 50-кубит. Даже если нам удастся использовать всю материю нашей вселенной для построения гигантского чипа памяти, основываясь на современных способах построения компьютерной памяти, то нам не удастся построить память для хранения 100-кубит. В то же время совокупность из 100 взаимодействующих фотонов - это то, что нас повсеместно окружает. Осознание того, что природа широко использует квантовые принципы работы, стало отправной точкой возникновения самой идеи квантовых вычислений.

Идея использования квантовых систем в вычислительных устройствах была независимо высказана в 1980 году Юрием Маниным и Паулем Бениофом (Yuri Manin, Раи1 Вепго). Эта идея также рассматривалась Рихардом Фейнманом (Richard Feynmann) в 1982 году Основания этой теории систематически разрабатывались Дэвидом Дейтчем (David Deutsch), но настоящий взрывной интерес к этой области появился с открытием алгоритма Шора в 1994 году Квантовый алгоритм, который разработал Питер Шор (Реег Shor), может взломать широко используемый в криптографии алгоритм шифрования с открытым ключом. Такой алгоритм сегодня повсеместно используется при передаче секретных данных в интернете. Конечно, для реализации алгоритма требуется построить достаточно большой квантовый компьютер, что пока технологически недостижимо.

Цель этого курса объяснить алгоритм Шора и все детали, требуемые для его понимания.