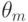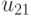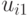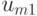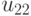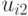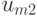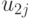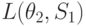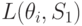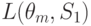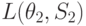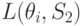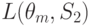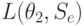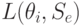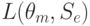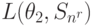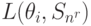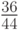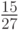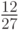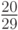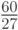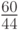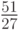|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Основные понятия теории статистических решений
Обоснование статистических решений при фиксированных экспериментах
Часто встречаются ситуации, когда на выбор решения существенное влияние оказывают факторы, информация о которых отсутствует или является недостаточно полной. Обоснование решений в этих условиях оказывается весьма эффективным с помощью статистических решений.
Сущность задач статистических решений состоит в том, что нужно сделать выбор из множества действий 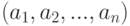 , эффективность каждого из которых зависит от того, какое из состояний "природы"
, эффективность каждого из которых зависит от того, какое из состояний "природы" 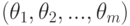 имеет место. Поэтому каждая пара
имеет место. Поэтому каждая пара 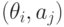 , состоящая из действия и состояния "природы", имея тот или иной исход, характеризуется значением критерия эффективности
, состоящая из действия и состояния "природы", имея тот или иной исход, характеризуется значением критерия эффективности 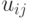 . Последнее приводит к
. Последнее приводит к 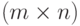 матрице (таблица 11.1), на основании которой нужно выбрать действие, являющееся оптимальным согласно некоторому критерию. Подобная матрица представляет стохастическую модель конфликтной ситуации, в которой одним из противников является "природа" (обстановка боевых действий, — Абчук В.А., Емельянов Л.А., Матвейчук Ф.А., Суздаль В.Г. Введение в теорию выработки решений. М., Военное издательство, 1972.). Обычно в теории статистических решений оперируют с критерием эффективности, характеризующим те или иные потери. Поэтому получаемую матрицу называют матрицей потерь.
матрице (таблица 11.1), на основании которой нужно выбрать действие, являющееся оптимальным согласно некоторому критерию. Подобная матрица представляет стохастическую модель конфликтной ситуации, в которой одним из противников является "природа" (обстановка боевых действий, — Абчук В.А., Емельянов Л.А., Матвейчук Ф.А., Суздаль В.Г. Введение в теорию выработки решений. М., Военное издательство, 1972.). Обычно в теории статистических решений оперируют с критерием эффективности, характеризующим те или иные потери. Поэтому получаемую матрицу называют матрицей потерь.
| Состояние "природы" | Действие | |||||
|---|---|---|---|---|---|---|
 |
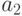 |
... | 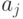 |
... | 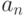 |
|
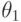
. . .
. . .
|

. . .
. . .
|
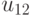
. . .
. . .
|
... ... ... ... |
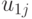
. . .
. . .
|
... ... ... ... |
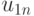
. . .
. . .
|
Поясним сказанное на следующем примере.
Предположим, что ракетная подводная лодка для нанесения удара по береговой цели должна занять огневую позицию в одном из трех районов. Каждый район огневых позиций 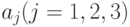 в зависимости от состояния моря
в зависимости от состояния моря 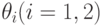 характеризуется математическим ожиданием числа непопадающих ракет
характеризуется математическим ожиданием числа непопадающих ракет 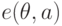 , величины которых определяются таблицей 11.2.
, величины которых определяются таблицей 11.2.
| Состояние "природы" | Действие | ||
|---|---|---|---|
| Район №1 | Район №2 | Район №3 | |
| Море 2 балла Море 5 |
0 5 |
1 3 |
3 2 |
Очевидно, если вероятности состояний "природы"  известны и равны соответственно
известны и равны соответственно 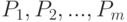 , где
, где 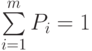 , то за критерий можно принять среднюю (ожидаемую) эффективность действия
, то за критерий можно принять среднюю (ожидаемую) эффективность действия 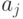 . Тогда выбирается действие, которое минимизирует данный критерий, и принимается , что это действие является оптимальным при данном априорном распределении вероятностей.
. Тогда выбирается действие, которое минимизирует данный критерий, и принимается , что это действие является оптимальным при данном априорном распределении вероятностей.
Так, если в рассматриваемом примере все состояния равновероятны, то следует выбрать действие 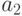 (район №2), поскольку в этом случае средняя эффективность будет равна
(район №2), поскольку в этом случае средняя эффективность будет равна 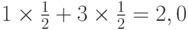 , тогда как при выборе
, тогда как при выборе  (района №1) или
(района №1) или  (района №3) она составит
(района №3) она составит  соответственно.
соответственно.
Таким образом, допущение априорного распределения вероятностей дает довольно простой метод выбора оптимального решения. Однако на практике истинное распределение вероятностей состояний "природы", как правило, неизвестно. В связи с этим целесообразно поставить эксперимент для оценки состояния "природы".
Предположим, что в рассматриваемом примере таким экспериментом является измерение атмосферного давления.
Пусть 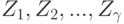 — множество возможных исходов, и известна вероятность
— множество возможных исходов, и известна вероятность  каждого исхода для каждого истинного состояния природы. Допустим
каждого исхода для каждого истинного состояния природы. Допустим 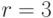 и примем значения вероятности
и примем значения вероятности  , равным приведенным в таблице 11.3.
, равным приведенным в таблице 11.3.
| Состояние "природы" | Наблюдение | ||
|---|---|---|---|
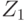 |
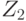 |
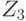 |
|
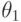
|
0,60 0,20 |
0,25 0,30 |
0,15 0,50 |
Теперь в зависимости от результатов эксперимента можно перечислить все возможные стратегии выбора района огневых позиций. Так, например, одной из стратегий может быть следующий план: выбрать район №1 (действие  ), если результат эксперимента
), если результат эксперимента 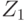 ; район №2 (действие
; район №2 (действие 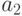 ), если результат эксперимента
), если результат эксперимента 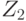 ; район №3, если результат эксперимента
; район №3, если результат эксперимента 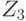 .
.
Каждая такая стратегия представляет систему:
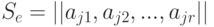 |
( 11.1) |
где 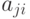 — действие, предпринимаемое при наблюдении
— действие, предпринимаемое при наблюдении 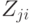
 — номер действия
— номер действия 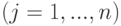 ;
;
 — номер стратегии
— номер стратегии 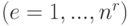 ;
;
 — номер эксперимента
— номер эксперимента 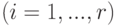 .
.
Иными словами, стратегия – это функция, определенная на пространстве выбора эксперимента  , значения которой суть действия
, значения которой суть действия 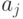 . Поскольку каждому исходу эксперимента соответствует
. Поскольку каждому исходу эксперимента соответствует  возможных действий, при
возможных действий, при  возможных исходных имеется
возможных исходных имеется 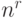 возможных стратегий. Для рассматриваемого примера
возможных стратегий. Для рассматриваемого примера 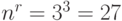 (таблица 11.4).
(таблица 11.4).
| Наблюдение | Стратегия | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
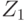
|
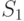 |
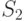 |
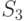 |
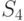 |
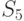 |
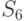 |
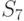 |
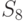 |
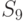 |
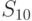 |
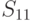 |
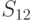 |
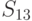 |
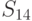 |

|

|

|

|

|

|

|

|

|
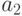
|
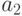
|
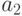
|
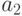
|
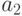
|
|
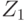
|
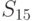 |
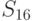 |
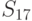 |
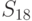 |
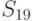 |
 |
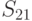 |
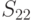 |
 |
 |
 |
 |
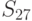 |
|
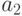
|
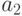
|
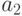
|
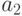
|

|

|

|

|

|

|

|

|

|
||
Из анализа таблицы видно, что некоторые из стратегий совершенно не учитывают исход эксперимента, например,  ; другие — учитывают в определенной степени и так далее. Однако каждая стратегия в зависимости от истинного состояния "природы" приводит к тем или иным результатам. Для вычисления этого результата с учетом эксперимента определим его вероятность
; другие — учитывают в определенной степени и так далее. Однако каждая стратегия в зависимости от истинного состояния "природы" приводит к тем или иным результатам. Для вычисления этого результата с учетом эксперимента определим его вероятность 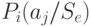 как вероятность того, что, когда истинное состояние "природы" есть
как вероятность того, что, когда истинное состояние "природы" есть 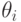 , эксперимент
, эксперимент  приводит к исходу, с которым стратегия
приводит к исходу, с которым стратегия 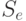 связывает действие
связывает действие 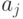 . Очевидно, что
. Очевидно, что  . Так, например, из описания стратегии
. Так, например, из описания стратегии 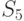 (таблица 11.4) видно, что если результатом эксперимента будет
(таблица 11.4) видно, что если результатом эксперимента будет 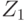 , то выбирается действи
, то выбирается действи  , если
, если 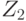 или
или 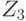 , — действие
, — действие 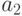 . Для состояния природы
. Для состояния природы 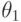 исход эксперимента
исход эксперимента 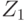 возможен с вероятностью 0.60 (таблица 11.3), а
возможен с вероятностью 0.60 (таблица 11.3), а 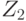 или
или 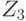 — с вероятностью 0,40. Следовательно,
— с вероятностью 0,40. Следовательно,
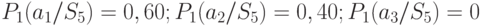 .
.
Аналогично для состояния "природы" 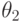 получим:
получим:
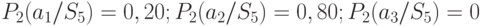 .
.
Теперь можно определить средние потери для каждой стратегии 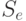 , когда истинное состояние "природы" есть
, когда истинное состояние "природы" есть 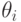 .
.
Так как следствием пары 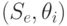 являются результаты
являются результаты 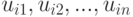 , а вероятность пар "действие – состояние"
, а вероятность пар "действие – состояние" 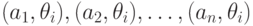 равны
равны 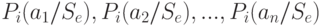 , то средние потери для стратегии
, то средние потери для стратегии 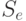 будут:
будут:
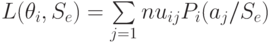 |
( 11.2) |
где 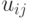 — потери при выборе действия
— потери при выборе действия 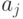 и истинном состоянии "природы"
и истинном состоянии "природы" 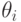 .
.
На основании (11.2.) можно вычислить матрицу средних потерь.
| Состояние "природы" | Стратегия | |||||
|---|---|---|---|---|---|---|
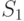 |
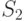 |
... | 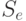 |
... | 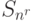 |
|
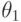
. . .
. . .
|
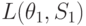
. . .
. . .
|
L(\theta_1,S_2)
. . .
. . .
|
... ... ... ... |
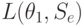
. . .
. . .
|
... ... ... ... |
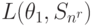
. . .
. . .
|
Для условий рассматриваемого примера вычисление средних потерь по формуле (11.2.) приводит к таблице 11.6.
| Состояние "природы" | Стратегия | ||||||||
|---|---|---|---|---|---|---|---|---|---|
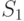 |
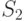 |
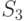 |
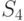 |
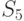 |
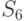 |
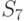 |
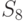 |
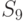 |
|
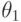
|
0,00 5,00 |
0,15 4,00 |
0,45 3,50 |
0,25 4,40 |
0,40 3,40 |
0,70 2,90 |
0,75 4,10 |
0,90 3,10 |
1,20 2,60 |
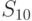 |
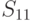 |
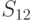 |
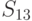 |
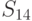 |
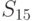 |
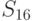 |
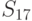 |
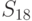 |
|
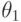
|
0,60 4,60 |
0,75 3,60 |
1,05 3,10 |
0,85 4,00 |
1,00 3,00 |
1,30 2,50 |
1,35 3,70 |
1,50 2,70 |
1,80 2,20 |
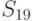 |
 |
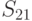 |
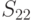 |
 |
 |
 |
 |
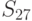 |
|
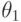
|
1,80 4,40 |
1,95 3,40 |
2,25 2,90 |
2,05 3,80 |
2,20 2,80 |
2,50 2,30 |
2,55 3,50 |
2,70 2,50 |
3,00 2,00 |
Матрица средних потерь (табл. 11.5) представляет собой модель конфликтной ситуации при фиксированных экспериментах. В связи с этим первоначальная задача статического решения модифицируется, сводясь к выбору одной из стратегий 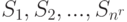 для состояний "природы"
для состояний "природы"  .
.
Предположим теперь, что даны априорные вероятности состояний "природы" 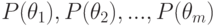 . После постановки эксперимента, исход которого зависит от истинного состояния "природы", значения вероятностей состояний изменяются и по формуле Байеса будут равны
. После постановки эксперимента, исход которого зависит от истинного состояния "природы", значения вероятностей состояний изменяются и по формуле Байеса будут равны
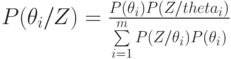 |
( 11.3) |
где 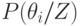 — апостериорная вероятность состояния
— апостериорная вероятность состояния 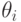 ;
;
 — вероятность исхода
— вероятность исхода  для истинного состояния
для истинного состояния 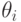 .
.
Если теперь принять, что 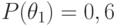 и
и 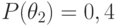 , то апостериорные вероятности состояний примут значения, приведенные в таблице 11.7.
, то апостериорные вероятности состояний примут значения, приведенные в таблице 11.7.
В результате приходим к первоначальной задаче оптимального выбора действия, когда вероятности состояний "природы" известны и равны 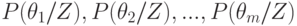 .
.
На основании этого можно определить средние потери для действия 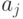 с учетом эксперимента
с учетом эксперимента  по формуле
по формуле
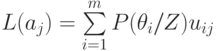 |
( 11.4) |
где 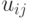 — потери пары "действие – состояние"
— потери пары "действие – состояние" 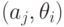 .
.
Оптимальным в этом случае будет действие, дающее наименьшие потери. Для нашего примера расчеты, выполненные по формуле 11.4., сведены в таблицу 11.8.
Из таблицы 11.8 видно, что в случае исхода 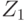 оптимальным является действие a_1, исхода
оптимальным является действие a_1, исхода 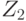 — действие
— действие 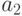 и исхода
и исхода 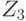 — действие
— действие  .
.
Таким образом, получено правило, в соответствии с которым каждому исходу эксперимента  соответствует действие
соответствует действие  , дающее минимальные потери. Это правило называется правилом Байеса относительно априорного распределения вероятностей состояний природы, а действие — байесовым. Так, для рассматриваемого примера, если исход эксперимента
, дающее минимальные потери. Это правило называется правилом Байеса относительно априорного распределения вероятностей состояний природы, а действие — байесовым. Так, для рассматриваемого примера, если исход эксперимента 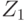 , байесовым действием является действие
, байесовым действием является действие  , если исход
, если исход 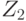 — действие
— действие 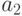 и если исход
и если исход 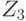 — действие
— действие  .
.
Байесовое действие входит в байесовую стратегию, которая минимизирует среднее взвешенное
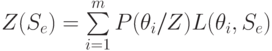 |
( 11.5) |
и соответствует вероятности 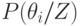 .
.
В этом можно убедиться, если по формуле (11.4.) произвести вычисление, используя данные таблицы 11.5 – 11.7, и выбрать стратегию, для которой 
будет минимальным. Такой байесовой стратегией окажется 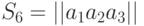 . Из описания стратегии
. Из описания стратегии 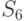 видно, что если исход эксперимента
видно, что если исход эксперимента 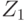 , то выбирается действие
, то выбирается действие  , если
, если 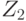 , то действие
, то действие 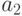 , и если
, и если 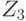 , то действие
, то действие  , то есть байесовые действия.
, то есть байесовые действия.
Таким образом, задаваясь априорным распределением вероятностей состояния природы, возможно их уточнить путем постановки эксперимента и определения апостериорных вероятностей.
Теорема Байеса. Пусть 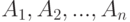 — взаимоисключающие события. Объединение всех
— взаимоисключающие события. Объединение всех  образует достоверное событие, полную группу событий. Тогда теорема Байеса гласит: вероятность того, что событие
образует достоверное событие, полную группу событий. Тогда теорема Байеса гласит: вероятность того, что событие  наступит при условии, что событие E уже наступило, определяется выражением
наступит при условии, что событие E уже наступило, определяется выражением
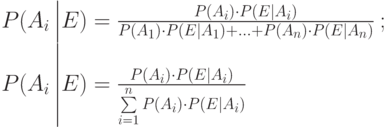 |
( 11.15) |