|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Прикладные задачи дискретного программирования
Задача теории расписаний
Общая задача теории расписаний. В отечественной литературе эту задачу обычно называют задачей календарного планирования. Общую ее схему можно описать следующим образом. Имеется m станков и n деталей, каждая из которых должна пройти обработку на всех станках в определенном порядке. Этот порядок может быть одинаковым для всех деталей либо различным для разных их групп. При этом производственные операции считаются неделимыми (начав обработку детали  на станке
на станке  , мы должны довести эту обработку до конца, не имея права прервать ее).
, мы должны довести эту обработку до конца, не имея права прервать ее).
Задана матрица 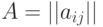 , где
, где  — время, необходимое для обработки
— время, необходимое для обработки  -й детали на
-й детали на  -м станке
-м станке 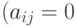 для тех деталей
для тех деталей  , которые не требуют обработки на станке
, которые не требуют обработки на станке  ). Требуется указать такой порядок запуска деталей в обработку, который минимизировал бы общее время выполнения всех работ (длину производственного цикла).
). Требуется указать такой порядок запуска деталей в обработку, который минимизировал бы общее время выполнения всех работ (длину производственного цикла).
Непосредственному решению (путем перебора всех вариантов) эта задача не поддается, так как при этом уже в простейшем случае одинакового порядка прохождения деталей пришлось бы выбирать наименьшую из  ! величин. При больших
! величин. При больших  это практически неосуществимо даже с использованием быстродействующих электронных машин. Несмотря на огромное прикладное значение этой задачи (описанная модель или ее варианты являются схемами основной массы задач по организации производства), пока удалось получить ее решение только для случая двух машин (алгоритм Джонсона, лекция №17)
это практически неосуществимо даже с использованием быстродействующих электронных машин. Несмотря на огромное прикладное значение этой задачи (описанная модель или ее варианты являются схемами основной массы задач по организации производства), пока удалось получить ее решение только для случая двух машин (алгоритм Джонсона, лекция №17)  . Вместе с тем случай
. Вместе с тем случай  до сих пор доставлял весьма серьезные теоретические и вычислительные затруднения. Постановка задач этого класса в виде целочисленных задач линейного программирования является одним из перспективных путей продвижения в этом направлении.
до сих пор доставлял весьма серьезные теоретические и вычислительные затруднения. Постановка задач этого класса в виде целочисленных задач линейного программирования является одним из перспективных путей продвижения в этом направлении.
Известно несколько формулировок задачи теории расписаний в виде целочисленных задач линейного программирования. Опишем одну из возможных постановок для которой является идея А. С. Мэн ( Мэн А.С. Задача календарного планирования для предприятий единичного и мелкосерийного производства. Сб. "Календарное планирование", М. , "Прогресс", 1966, гл.12.).
Одна из возможных постановок задачи теории расписаний.
Не умаляя общности, можно считать 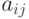 целыми числами. Составление графика обработки деталей будем связывать с "календарем", "дни" которого занумерованы целыми числами
целыми числами. Составление графика обработки деталей будем связывать с "календарем", "дни" которого занумерованы целыми числами 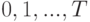 , где
, где  настолько велико, чтобы заведомо обеспечить возможность обработки всей партии.
настолько велико, чтобы заведомо обеспечить возможность обработки всей партии.
Введем неотрицательные целочисленные переменные , принимающие значения 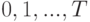 . Здесь
. Здесь 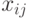 указывает "дату" начала обработки
указывает "дату" начала обработки  -м станком
-м станком  -й детали. Рассмотрим условия, которым должны удовлетворять
-й детали. Рассмотрим условия, которым должны удовлетворять 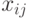 .
.
-
Прежде всего нужно наложить ограничение, не допускающее одновременной обработки на одном станке двух деталей. Для этого моменты начала обработки любых двух деталей
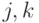 должны отстоять по "календарю" не менее чем на длительность обработки той из них, которая запускается первой, то есть
должны отстоять по "календарю" не менее чем на длительность обработки той из них, которая запускается первой, то есть
( 7.25) В обычную задачу линейного программирования альтернативное условие типа (7.25.) ввести нельзя. Определим целочисленные переменные
 , принимающие значения 0 или 1. Тогда (7.25.) можно переписать в виде,
, принимающие значения 0 или 1. Тогда (7.25.) можно переписать в виде,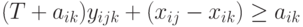
( 7.26) 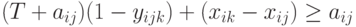
( 7.27) Отметим очевидное неравенство
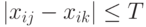 , вытекающее из определения
, вытекающее из определения  . Ясно, что случай
. Ясно, что случай 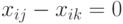 невозможен, то есть обработка двух разных деталей не может начаться на одном станке одновременно, ибо в этом случае неравенства (7.26.) удовлетворялись бы только при
невозможен, то есть обработка двух разных деталей не может начаться на одном станке одновременно, ибо в этом случае неравенства (7.26.) удовлетворялись бы только при 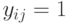 , а неравенства (7.27.) – только при
, а неравенства (7.27.) – только при 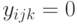 . Если
. Если 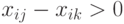 , то
, то  в (7.26.) может быть равен нулю или единице, а в (7.27 ) – только нулю, так что единственным возможным значением здесь будет
в (7.26.) может быть равен нулю или единице, а в (7.27 ) – только нулю, так что единственным возможным значением здесь будет 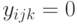 . Если же
. Если же 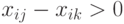 , то
, то  в (7.26.) может быть равен только единице, а в (7.27.) и нулю и единице, так что в этом случае возможно лишь
в (7.26.) может быть равен только единице, а в (7.27.) и нулю и единице, так что в этом случае возможно лишь 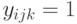 .
.Отсюда ясно, что
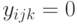 , если на
, если на  -м станке обработка
-м станке обработка  -й детали предшествует обработке
-й детали предшествует обработке  -й детали, и
-й детали, и 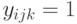 в противном случае.
в противном случае. -
Теперь следует отразить условия на заданный технологический порядок прохождения деталями обработки на станках. В данной формулировке в принципе безразлично, является ли этот порядок одинаковым для всех деталей или нет. Именно, если деталь должна быть обработана сначала на станке
 , затем на станке
, затем на станке  , то мы должны иметь.
, то мы должны иметь.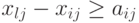
( 7.28) Отсюда ясно, что случай
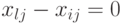 , то есть одновременное начало обработки одной детали на двух станках, возможен лишь при
, то есть одновременное начало обработки одной детали на двух станках, возможен лишь при 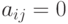 , то есть тогда, когда данная деталь на одном из этих станков вообще не должна обрабатываться.
, то есть тогда, когда данная деталь на одном из этих станков вообще не должна обрабатываться.Для некоторых деталей условие упорядочения может налагаться лишь в следующей ослабленной форме: деталь
 должна пройти обработку на станках
должна пройти обработку на станках 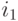 и
и 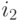 , в любом порядке, затем на станке
, в любом порядке, затем на станке  . Тогда условие (7.29.) заменится следующими двумя условиями:
. Тогда условие (7.29.) заменится следующими двумя условиями: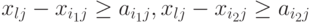
( 7.29) Можно дать еще вариант условий этого типа, считая что деталь
 между обработкой на станках
между обработкой на станках  и
и  должна пролежать время
должна пролежать время 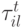 (целое число) . В этом случае.
(целое число) . В этом случае.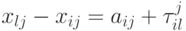
( 7.30) -
Могут быть наложены дополнительные условия "на отправку" (то есть на сроки окончания отдельных работ). Так, если обработка детали
 на станке
на станке  должна быть закончена к сроку
должна быть закончена к сроку 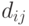 , то.
, то.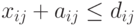
( 7.31) -
В качестве критерия оптимальности принимается минимизация общего времени обработки партии. Пусть
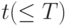 — дата полного завершения работ. Нужно минимизировать
— дата полного завершения работ. Нужно минимизировать  при условиях
при условиях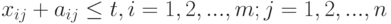
( 7.32) и при условиях (7.26.), (7.27.), (7.28.) или его вариантах и, возможно, еще при условиях (7.31.).
Всего в этой модели приходится вводить 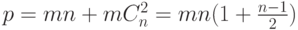 переменных (не считая
переменных (не считая  и свободных переменных). Эти переменные, кроме того, должны быть целочисленными. Для реальных задач даже самых скромных размеров это приводит к весьма громоздким моделям (так, при
и свободных переменных). Эти переменные, кроме того, должны быть целочисленными. Для реальных задач даже самых скромных размеров это приводит к весьма громоздким моделям (так, при 
и 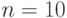 мы получаем
мы получаем 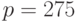 ).
).
Однако описанная модель, по-видимому, является одной из наиболее экономных в смысле размеров получающейся целочисленной задачи. Интересующийся теорией расписаний может посмотреть книгу Шурба В.В., Подчасова Т.П., Пшичук А.Н., Тур Л.П. , Задачи календарного планирования и методы их решения. (Киев, "Наукова думка", 1966.).
Задача о наилучшем распределении памяти вычислительной машины
Рассмотрим следующую упрощенную задачу о наилучшем распределении памяти вычислительной машины. Пусть 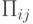 —
—  -я стандартная подпрограмма для вычисления функции
-я стандартная подпрограмма для вычисления функции  в библиотеке подпрограмм
в библиотеке подпрограмм 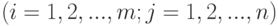 . Подпрограмма
. Подпрограмма 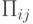 занимает
занимает 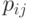 ячеек памяти и требует для счета
ячеек памяти и требует для счета 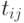 секунд. Требуется составить "программу"
секунд. Требуется составить "программу"  , которая определяется заданием некоторого набора
, которая определяется заданием некоторого набора  индексов
индексов  , то есть функций, подлежащих вычислению (наличием иных команд пренебрегаем). При этом следует для составления программы
, то есть функций, подлежащих вычислению (наличием иных команд пренебрегаем). При этом следует для составления программы  указать такой набор подпрограмм
указать такой набор подпрограмм 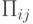 , чтобы длина всей программы не превосходила M ячеек, а время счета по ней было минимальным.
, чтобы длина всей программы не превосходила M ячеек, а время счета по ней было минимальным.
Как обычно в подобных случая, вводим переменные
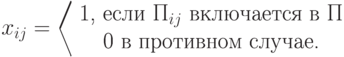 |
( 7.33) |
Тогда наша задача сведется к минимизации
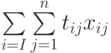 |
( 7.34) |
при условиях
 |
( 7.35) |
Задача финансирования исследовательских проектов
Рассмотрим финансирование исследовательских проектов. Пусть на протяжении  лет возможно осуществление исследовательских проектов. Ожидаемый эффект проекта
лет возможно осуществление исследовательских проектов. Ожидаемый эффект проекта  , выраженный в "сегодняшних" единицах полезности, составляет
, выраженный в "сегодняшних" единицах полезности, составляет 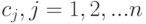 . Затраты в год
. Затраты в год  на осуществление проекта
на осуществление проекта  составляют
составляют 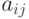 , а общий лимит капиталовложений на исследования в году
, а общий лимит капиталовложений на исследования в году  равен
равен 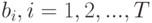 . Требуется указать максимально эффективный набор проектов, не выводящий за пределы отпускаемых вложений.
. Требуется указать максимально эффективный набор проектов, не выводящий за пределы отпускаемых вложений.
Формализация этой задачи очевидна: если обычным образом ввест переменные
 |
( 7.36) |
то мы придем к задаче максимизации
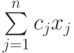
при условиях
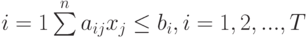 |
( 7.37) |
Задача из области экономики сельского хозяйства
Рассмотрим следующую упрощенную статическую модель распределения тракторных работ (Корбут А.А. Целочисленные задачи линейного программирования. В сб. "Эконом.-матем. методы", вып. 2, М., "Наука", 1965, 141-186.).
Имеется n типов сельскохозяйственных машин и m видов работ, подлежащих выполнению в объемах 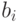 ,
, 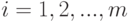 (будем считать, что все эти объемы выражены в гектарах). Заданы производительность
(будем считать, что все эти объемы выражены в гектарах). Заданы производительность  -й машины на
-й машины на  -й работе
-й работе 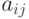 , а также себестоимость
, а также себестоимость 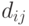 обработки одного гектара работы
обработки одного гектара работы  машиной
машиной  . Себестоимость самих машин (скажем, стоимость их покупки или аренды, взятая с некоторым коэффициентом приведения) составляет
. Себестоимость самих машин (скажем, стоимость их покупки или аренды, взятая с некоторым коэффициентом приведения) составляет 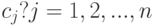 . Следует найти оптимальный машинный парк для данного комплекса работ и указать его распределение по работам. Чтобы выполнить задание и добиться минимальной суммарной себестоимости, обозначим через
. Следует найти оптимальный машинный парк для данного комплекса работ и указать его распределение по работам. Чтобы выполнить задание и добиться минимальной суммарной себестоимости, обозначим через 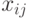 количество машин каждого типа, а через
количество машин каждого типа, а через 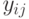 — количество машин типа
— количество машин типа  , которое будет выделено на работу
, которое будет выделено на работу  . Тогда наша задача сведется к минимизации
. Тогда наша задача сведется к минимизации
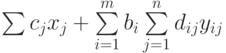 |
( 7.38) |
при условиях
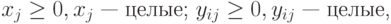 |
( 7.39) |
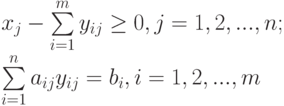 |
( 7.40) |
Отметим, что накладывать условие целочисленности на 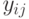 не обязательно, так как нецелые
не обязательно, так как нецелые 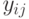 здесь вполне поддаются разумной интерпретации.
здесь вполне поддаются разумной интерпретации.
Таким образом, перед нами еще один пример задачи с неделимостями. Модель эта существенно усложнится, если дополнительно потребовать выполнения каждой работы в отведенные для нее агротехнические сроки; здесь мы не будем на этом останавливаться.

