| Азербайджан |
Линейный классификатор. Алгоритм персептрона
3.2. Алгоритм персептрона
3.2.1. Математическая модель нейрона. В алгоритме персептрона
в основу положен принцип действия нейрона. Обобщенная схема нейрона
представлена на рисунке. Здесь 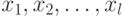 – компоненты вектора признаков
– компоненты вектора признаков 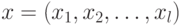 ;
;  –
сумматор;
–
сумматор; 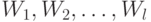 – синоптические веса;
– синоптические веса;  – функция активации;
– функция активации; 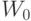 – порог.
Выходом сумматора является величина
– порог.
Выходом сумматора является величина  , которая является входом
(аргументом) функции активации. Значение функции активации вычисляется
на основе определения знака суммы
, которая является входом
(аргументом) функции активации. Значение функции активации вычисляется
на основе определения знака суммы 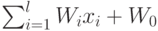 :
:

Таким образом, нейрон представляет собой линейный классификатор с
дискриминантной функцией 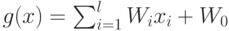 .
.
Тогда задача построения линейного классификатора для заданного
множества прецедентов сводится к задаче обучения нейрона, т.е. подбора
соответствующих весов 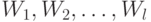 и порога
и порога 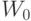 . Обучение состоит в коррекции
синоптических весов и порога.
. Обучение состоит в коррекции
синоптических весов и порога.
3.2.2. Алгоритм персептрона. Алгоритм персептрона представляет
собой последовательную итерационную процедуру. Каждый шаг состоит в
предъявлении нейрону очередного вектора-прецедента и коррекции весов 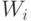 по результатам классификации. При этом прецеденты предъявляются
циклически, т.е. после предъявления последнего снова предъявляется
первый. Процесс обучения заканчивается, когда нейрон правильно
классифицирует все прецеденты.
по результатам классификации. При этом прецеденты предъявляются
циклически, т.е. после предъявления последнего снова предъявляется
первый. Процесс обучения заканчивается, когда нейрон правильно
классифицирует все прецеденты.
Обозначим 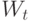 весовой вектор после
весовой вектор после  -й итерации, а
-й итерации, а 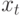 – прецедент,
предъявляемый на
– прецедент,
предъявляемый на  -й итерации.
-й итерации.
Основной шаг алгоритма состоит в предъявлении очередного
прецедента 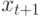 :
:
Если 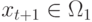 и
и 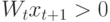 , то
, то 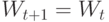 ;
;
Если 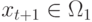 и
и 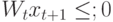 , то
, то 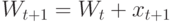 ;
;
Если 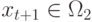 и
и 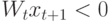 , то
, то 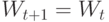 ;
;
Если 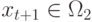 и
и 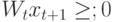 , то
, то 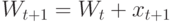 .
.
На данном рисунке 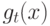 – дискриминантная функция после
– дискриминантная функция после  -го шага алгоритма;
-го шага алгоритма; 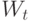 – весовой вектор после
– весовой вектор после  -го шага алгоритма.
-го шага алгоритма.



