НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 14: Классические и квантовые коды

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 15.03.2007 | Уровень: профессионал | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать программу

Анионы (иллюстративный пример на основе торического кода).

На примере торического кода можно дать более точное представление об анионных системах, о которых говорилось во введении.

Итак, вновь рассмотрим квадратную сетку на торе (а можно и на плоскости — сейчас нас будет интересовать только ее центральная часть). Как и раньше, для каждой вершины и каждой грани рассмотрим проверочные операторы

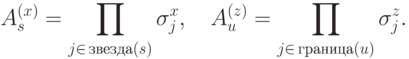
$A^{(x)}_s=\prod_{j\in\,\mathrm {\text {звезда}}(s)}^{} \sigma^x_j, \quad A^{(z)}_u=\prod_{j\in\,\mathrm {\text {граница}}(u)}^{} \sigma^z_j.$

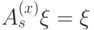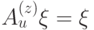Состояние кодового подпространства задается условиями $A^{(x)}_s\ket\xi=\ket\xi$ , $A^{(z)}_u\ket\xi=\ket\xi$ . Их можно переписать другим способом. Рассмотрим следующий гамильтониан — эрмитов оператор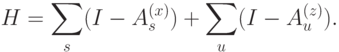

$H=\sum_{s}(I-A^{(x)}_s)+\sum_{u}(I-A^{(z)}_u).$

Этот оператор неотрицательный, причем его нулевое подпространство в точности совпадает с кодовым подпространством торического кода. Таким образом, векторы из кодового подпространства являются собственными и обладают наименьшей энергией (т.е. собственным числом гамильтониана). Такие векторы называются основными состояниями, а векторы из ортогонального дополнения — возбужденными состояниями.

Рассмотрим возбужденные состояния с наименьшей ненулевой энергией, когда нарушено ровно два условия (например, вершинных). (Число нарушенных условий каждого типа четное, поскольку 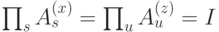$\prod_s A^{(x)}_s \double=\prod_u A^{(z)}_u=I$ .) Тогда для двух вершин, в которых кодовые условия нарушаются, выполнено

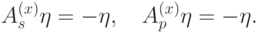
$A^{(x)}_s\ket\eta=-\ket\eta, \quad A^{(x)}_p\ket\eta=-\ket\eta.$

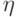Как можно получить состояние $\ket\eta$ из кодового состояния $\ket\xi$ ? Соединим

и

решеточным путем C_1

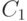и подействуем на 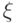$\ket\xi$ оператором $W=\prod_{j\in C_1}^{}\sz_j$ . Этот оператор коммутирует с проверочными вершинными операторами для всех промежуточных вершин пути C_1

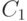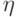, а в концах — антикоммутирует: $WA^{(x)}_s=-A^{(x)}_s W$ . Положим $\ket\eta=W\ket\xi$ и покажем, что $\ket\eta$ удовлетворяет требуемым свойствам. Для вершины

(аналогично и для

) имеем

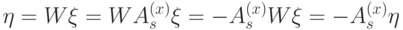
$\ket\eta=W\ket\xi =WA^{(x)}_s\ket\xi=-A^{(x)}_s W\ket\xi=-A^{(x)}_s\ket\eta$

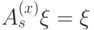( $A^{(x)}_s\ket\xi=\ket\xi$ , так как состояние 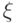$\ket\xi$ — кодовое).

Любое состояние системы можно построить из элементарных возбуждений двух типов, одни из которых "живут" на вершинах, другие — на гранях. Элементарное возбуждение — это просто нарушенное кодовое условие, но теперь мы думаем о нем как о частице. Частицы-возбуждения можно двигать, создавать и уничтожать. 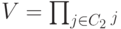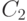Пара возбуждений первого типа получается из основного (кодового) состояния действием оператора , приведенного выше; пара возбуждений второго типа — действием оператора $V=\prod_{j\in C_2}^{}\sx_j$ , где C_2 — путь, соединяющий две грани, как показано на рис. 14.3a). Как и раньше проверяется, что $A^{(z)}_u(V\ket\xi)\double=-V\ket\xi$ .

Рис. 14.3.

Что случится, если двигать возбуждение одного типа (крестик) вокруг возбуждения второго типа (кружочка)? (См. рис. 14.3б).) Движение возбуждения описывается оператором 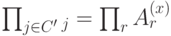$\prod_{j\in C'}\sx_j=\prod_r A^{(x)}_{r}$ , зависящим от контура обхода 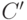(здесь пробегает все грани внутри 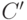). Очевидно, что 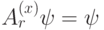$A^{(x)}_{r}\ket\psi=\ket\psi$ для всех 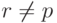$r\not=p$ . В результате мы получим

$\ket\psi\mapsto \prod_{j\in C'}^{}\sx_j\ket\psi = A^{(x)}_p\ket\psi = -\ket\psi.$

То есть вектор состояния домножился на

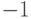. Это и означает, что рассматриваемые возбуждения являются (абелевыми) анионами.

На торе можно двигать частицы по двум различным циклам, образующим базис в группе гомологий. Например, можно создать из основного состояния пару возбуждений одного типа, обнести одно из возбуждений по циклу и проаннигилировать со вторым возбуждением. Этот процесс описывается некоторым оператором, действующим на кодовом подпространстве, — произведением 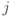$\sz_j$ вдоль пути на решетке, либо 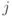$\sx_j$ вдоль пути на двойственной решетке. 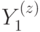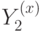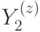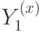Поскольку существует два типа возбуждений, мы имеем 4 таких оператора: $Y^{(z)}_1$ и $Y^{(x)}_2$ соответствуют одному базисному циклу, а $Y^{(z)}_2$ и $Y^{(x)}_1$ — другому. Эти операторы действуют на два закодированных q-бита как 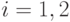$\sz_i, \sx_i$ ( i=1,2 ), потому что они обладают такими же коммутационными соотношениями: 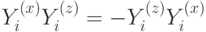$Y^{(x)}_i Y^{(z)}_i = -Y^{(z)}_i Y^{(x)}_i$ (остальные пары коммутируют).