Соотношение между классическим и квантовым вычислением
Классический объект, соответствующий унитарному оператору, — перестановка. Любой перестановке 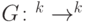 естественно сопоставляется унитарный оператор
естественно сопоставляется унитарный оператор 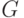 в пространстве
в пространстве 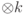 , действующий по правилу
, действующий по правилу  .
.
Аналогично определению 5.1, можно определить обратимые классические схемы, реализующие перестановки.
Определение 6.1. Обратимая классическая схема. Пусть  — некоторое множество перестановок вида
— некоторое множество перестановок вида 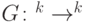 (базис). Обратимая классическая схема в базисе
(базис). Обратимая классическая схема в базисе  — это последовательность перестановок
— это последовательность перестановок ![U_1[A_1],\dots, U_l[A_l]](/sites/default/files/tex_cache/83f6be2593a816115df273c5dce4beff.png) , где
, где 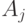 — множества битов,
— множества битов, 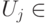 .
.
Перестановка, реализуемая обратимой схемой. Это произведение перестановок ![U_l[A_l]\cdot\ldots\cdot U_1[A_1]](/sites/default/files/tex_cache/775eb18f0bd0e4ef44cc3ecf4a874300.png) .
.
Перестановка  , реализуемая схемой в расширенном смысле. Это такая перестановка, что произведение перестановок
, реализуемая схемой в расширенном смысле. Это такая перестановка, что произведение перестановок
![W=U_l[A_l]\cdot\ldots\cdot U_1[A_1]](/sites/default/files/tex_cache/526cd679d7bedf77b6a7aab913526691.png)
 битов,
битов, 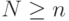 ) для любого
) для любого 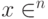 удовлетворяет условию
удовлетворяет условию  .
.В каких случаях функцию, заданную булевой схемой, можно реализовать обратимой схемой? Обратимые схемы реализуют только перестановки. Преодолеть эту трудность можно так. Вместо вычисления функции 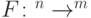 будем вычислять функцию
будем вычислять функцию 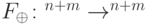 , заданную соотношением
, заданную соотношением 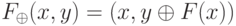 (здесь
(здесь  означает побитовое сложение по модулю 2). Тогда значение
означает побитовое сложение по модулю 2). Тогда значение 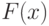 можно получить так:
можно получить так: 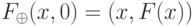 .
.
Чтобы можно было вычислять функции, заданные булевыми схемами в полном базисе, недостаточно взять базис для обратимых схем из перестановок на двух битах. Оказывается, что любая перестановка на двух битах 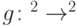 является линейной функцией (при естественном отождествлении множества
является линейной функцией (при естественном отождествлении множества  и поля из двух элементов
и поля из двух элементов 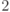 ):
):  , где
, где  ,
,  ,
,  ,
,  ,
,  ,
,  . Поэтому все функции, вычисляемые обратимыми схемами в базисе из перестановок на двух битах, являются линейными.
. Поэтому все функции, вычисляемые обратимыми схемами в базисе из перестановок на двух битах, являются линейными.
А вот перестановок на трех битах уже достаточно, чтобы реализовать любую функцию. При этом не обязательно использовать все перестановки, достаточно включить в базис лишь две функции — отрицание 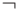 и элемент Тоффоли
и элемент Тоффоли 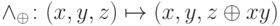 . При этом имеется в виду реализуемость в расширенном смысле, т.е. можно брать напрокат биты в состоянии 0 и возвращать их после окончания вычислений в том же состоянии.
. При этом имеется в виду реализуемость в расширенном смысле, т.е. можно брать напрокат биты в состоянии 0 и возвращать их после окончания вычислений в том же состоянии.
Задача 6.1. Докажите для обратимых схем полноту базиса, состоящего из отрицания и элемента Тоффоли.
Лемма 6.1. Пусть функция 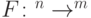 реализуется булевой схемой размера
реализуется булевой схемой размера  в некотором базисе
в некотором базисе  . Тогда можно реализовать функцию
. Тогда можно реализовать функцию  обратимой схемой размера
обратимой схемой размера 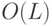 в базисе {
в базисе {  , состоящем из функций
, состоящем из функций 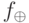 (
( 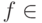 ), а также функции
), а также функции 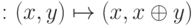 .
.
Замечание 6.1. Помимо "полезного" ответа 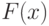 схема, указанная в формулировке леммы, производит "мусор"
схема, указанная в формулировке леммы, производит "мусор" 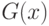 .
.
Замечание 6.2. Содержательный смысл операции  — обратимое копирование бита (если начальное значение
— обратимое копирование бита (если начальное значение  равно
равно  ). В литературе эта операция обычно называется Controlled NOT по причинам, которые станут ясными из дальнейшего.
). В литературе эта операция обычно называется Controlled NOT по причинам, которые станут ясными из дальнейшего.
Замечание 6.3. Применяя функцию 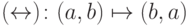 можно менять биты местами в записи. Обратите внимание, что для перестановок битов достаточно также иметь в базисе
можно менять биты местами в записи. Обратите внимание, что для перестановок битов достаточно также иметь в базисе  , так как
, так как
![(\leftrightarrow)[j,k]\double=\null\qxor[j,k]\qxor[k,j]\qxor[j,k].](/sites/default/files/tex_cache/4e6827f1e29d3a185608c1458e5fd9df.png)
Доказательство. Возьмем схему, вычисляющую  . Пусть входные переменные — это
. Пусть входные переменные — это  . Вспомогательные переменные схемы и биты результата — это
. Вспомогательные переменные схемы и биты результата — это 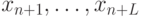 ; в обратимой схеме сопоставим им дополнительные биты, имеющие в начальном состоянии значение 0.
; в обратимой схеме сопоставим им дополнительные биты, имеющие в начальном состоянии значение 0.
Каждое присваивание в схеме имеет вид 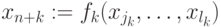 ,
, 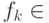 ,
, 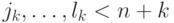 . В обратимой схеме аналогом присваивания будет действие перестановки
. В обратимой схеме аналогом присваивания будет действие перестановки 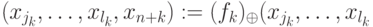 ,
, 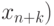 , т.е.
, т.е. 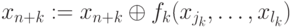 .
.
Поскольку начальные значения дополнительных переменных были равны 0, их конечные значения будут такими же, как и в булевой схеме.
Осталось поменять местами биты, чтобы получить указанный в условии формат ответа.
Весь процесс вычисления удобно представить следующей схемой (над прямоугольниками подписано количество битов, внутри — их содержимое):

