Классические и квантовые коды
Как уже обсуждалось ранее, квантовое вычисление "не слишком" чувствительно к погрешностям реализации унитарных операторов: ошибки накапливаются линейно. Если есть последовательность унитарных операторов 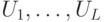 и последовательность приближений
и последовательность приближений 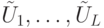 ,
, 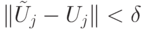 , то выполняется неравенство
, то выполняется неравенство
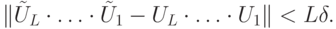
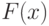 квантовой схемой
квантовой схемой  (см. определение 8.1). Эта вероятность (левая часть неравенства в определении) может быть записана как
(см. определение 8.1). Эта вероятность (левая часть неравенства в определении) может быть записана как  , где
, где  , а
, а  . Имеет место следующая оценка:
. Имеет место следующая оценка:
 ; в общем случае эта оценка неулучшаема.
; в общем случае эта оценка неулучшаема.С точки зрения физической реализации квантового компьютера, полученный результат не является удовлетворительным. Получается, что размер квантовой схемы  не должен превосходить
не должен превосходить 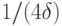 , иначе вероятность правильного ответа может стать меньше
, иначе вероятность правильного ответа может стать меньше 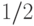 . Поэтому возникает важный вопрос: можно ли избежать накопления ошибок, используя схемы специального вида?
. Поэтому возникает важный вопрос: можно ли избежать накопления ошибок, используя схемы специального вида?
Ответ на этот вопрос положительный. Идея состоит в том, чтобы закодировать (заменить) каждый q-бит, использующийся в вычислениях, несколькими при помощи определенного изометрического вложения  . Дело в том, что ошибки, как правило, действуют одновременно на небольшое число q-битов, поэтому кодирование повышает устойчивость квантового состояния.
. Дело в том, что ошибки, как правило, действуют одновременно на небольшое число q-битов, поэтому кодирование повышает устойчивость квантового состояния.
Конструкции, необходимые для организации вычислений без потери точности, довольно сложны. Подробно они изложены в [41, 19, 34, 4, 32], а здесь мы в основном ограничимся более простым вопросом: как сохранять неограниченно долго заданное квантовое состояние? (Легко понять, что это — частный случай предыдущего вопроса, когда реализуется последовательность тождественных операторов.) Для решения такой упрощенной задачи конкретный вид кодирующего отображения  неважен; нужно задать лишь подпространство
неважен; нужно задать лишь подпространство 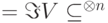 .
.
Определение 14.1. Квантовый код типа  — это подпространство
— это подпространство  размерности
размерности 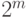 . (Число
. (Число  — количество закодированных q-битов — не обязательно должно быть целым).
— количество закодированных q-битов — не обязательно должно быть целым).
Ошибки, возникающие при хранении информации, будут приводить к тому, что состояние системы будет выходить за пределы  . Поэтому необходимо научиться восстанавливать состояние системы после воздействия ошибок определенного типа.
. Поэтому необходимо научиться восстанавливать состояние системы после воздействия ошибок определенного типа.
Классические коды.
Вначале рассмотрим случай классических кодов. Мы лишь слегка затронем эту обширную тему. Подробное изложение теории кодов, корректирующих ошибки, (так обычно называется эта наука) можно найти в [9].
Классический код типа  — это подмножество
— это подмножество 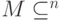 мощности
мощности 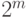 . Для описания ошибок необходимо также определить канал связи — нечто вроде неоднозначного отображения
. Для описания ошибок необходимо также определить канал связи — нечто вроде неоднозначного отображения 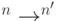 . Существует две модели ошибок: более реалистичная — вероятностная, и упрощенная — теоретико-множественная. Согласно вероятностной модели, канал связи задается условными вероятностями
. Существует две модели ошибок: более реалистичная — вероятностная, и упрощенная — теоретико-множественная. Согласно вероятностной модели, канал связи задается условными вероятностями  приема слова
приема слова  при передаче слова
при передаче слова  . Мы будем рассматривать случай независимо распределенных ошибок, полагая что
. Мы будем рассматривать случай независимо распределенных ошибок, полагая что  , а условные вероятности определяются через вероятность ошибки при передаче одного бита
, а условные вероятности определяются через вероятность ошибки при передаче одного бита 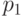 :
:
 |
( 14.1) |
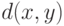 — расстояние Хэмминга (число различных битов).
— расстояние Хэмминга (число различных битов).Есть стандартный способ упростить модель независимо распределенных ошибок. Оценим вероятность того, что случится более  ошибок (как ясно из формулы (14.1), эта величина от
ошибок (как ясно из формулы (14.1), эта величина от  не зависит). Считаем, что
не зависит). Считаем, что 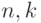 — фиксированы,
— фиксированы, 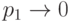 . Тогда
. Тогда
![\begin{equation}\label{k-errors} \Pr[\text{число ошибок}\,>k]=\sum_{j>k}^{} \binom{n}{j}p_1^j(1-p_1)^{n-j}= o(p_1^k). \end{equation}](/sites/default/files/tex_cache/618cc7e8254d55eabc57c3c3b35d6a21.png) |
( 14.2) |
 , мала. Поэтому можно сильно упростить модель. Будем считать, что при передаче слова
, мала. Поэтому можно сильно упростить модель. Будем считать, что при передаче слова  может получиться любое слово
может получиться любое слово  , такое что
, такое что 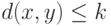 (параметр
(параметр  задает интересующий нас порог точности), а другие ошибки не встречаются.
задает интересующий нас порог точности), а другие ошибки не встречаются.Введем обозначения:
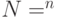 — множество входов,
— множество входов,
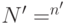 — множество выходов,
— множество выходов,
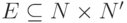 — множество переходов (оно же — множество ошибок),
— множество переходов (оно же — множество ошибок),
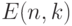 — множество
— множество  .
.
Определение 14.2. Код  исправляет ошибки из множества
исправляет ошибки из множества  , если для любых
, если для любых  из
из 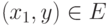 и
и 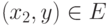 следует
следует  .
.
Другими словами это условие можно сформулировать так: для любых пар 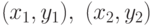 , принадлежащих
, принадлежащих  , из
, из  и
и  следует
следует 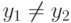 .
.
В том случае, когда  , говорят, что код исправляет k ошибок.
, говорят, что код исправляет k ошибок.
Замечание. Термин "код, исправляющий ошибки" является неточным. Правильнее было бы сказать, что код оставляет возможность для исправления ошибок. Исправляющие преобразование — это отображение 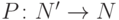 , такое что, если
, такое что, если  и
и 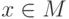 , то
, то  , вычисление значения исправляющего преобразования называется декодированием.
, вычисление значения исправляющего преобразования называется декодированием.
Пример 14.1. Код с повторением:
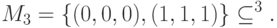
Очевидное обобщение примера 14.1 приводит к классическим кодам, исправляющим любое количество ошибок. Построим более интересные примеры классических кодов. Для начала дадим еще одно стандартное определение.
Определение 14.3. Кодовое расстояние — это
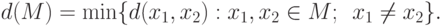
Для кода из примера 14.1 кодовое расстояние равно 3. Имеется очевидное утверждение.
Утверждение 14.1. Код исправляет  ошибок тогда и только тогда, когда
ошибок тогда и только тогда, когда 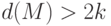 .
.
