|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Раскраски
Переборный алгоритм для раскраски
Рассмотрим алгоритм решения задачи о раскраске, похожий на описанный выше алгоритм для задачи о независимом множестве. Сходство заключается в том, что задача для данного графа сводится к той же задаче для двух других графов. Поэтому снова возникает дерево вариантов, обход которого позволяет найти решение. Но есть и одно существенное различие, состоящее в том, что теперь два новых графа не будут подграфами исходного графа.
Выберем в данном графе  две несмежные вершины
две несмежные вершины  и
и  и построим два новых графа:
и построим два новых графа: 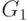 , получающийся добавлением
ребра
, получающийся добавлением
ребра 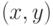 к графу
к графу  , и
, и 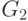 ,
получающийся из
,
получающийся из  слиянием вершин
слиянием вершин  и
и  . Операция слияния состоит
в удалении вершин
. Операция слияния состоит
в удалении вершин  и
и  и добавлении новой
вершины
и добавлении новой
вершины  и ребер, соединяющих ее с каждой вершиной,
с которой была смежна хотя бы
одна из вершин
и ребер, соединяющих ее с каждой вершиной,
с которой была смежна хотя бы
одна из вершин  ,
,  . На рис. 10.2
показаны графы
. На рис. 10.2
показаны графы 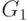 и
и 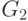 , получающиеся из
графа
, получающиеся из
графа  , изображенного на рис. 10.1,
с помощью этих операций, если в качестве
, изображенного на рис. 10.1,
с помощью этих операций, если в качестве  и
и  взять
вершины
взять
вершины  и
и  .
.
Если в правильной раскраске графа  вершины
вершины  и
и  имеют разные цвета, то она будет правильной и для графа
имеют разные цвета, то она будет правильной и для графа 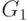 .
Если
же цвета вершин
.
Если
же цвета вершин  и
и  в раскраске
графа
в раскраске
графа  одинаковы, то граф
одинаковы, то граф 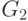 можно раскрасить в то же число цветов:
новая вершина
можно раскрасить в то же число цветов:
новая вершина  окрашивается в тот цвет, в который окрашены
вершины
окрашивается в тот цвет, в который окрашены
вершины  и
и  , а все остальные вершины сохраняют
те цвета,
которые они имели в графе
, а все остальные вершины сохраняют
те цвета,
которые они имели в графе  . И наоборот, раскраска каждого из
графов
. И наоборот, раскраска каждого из
графов 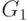 ,
, 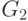 , очевидно, дает раскраску
графа
, очевидно, дает раскраску
графа  в то же число цветов. Поэтому
в то же число цветов. Поэтому
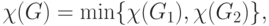
что дает возможность рекурсивного нахождения раскраски графа
в минимальное число цветов. Заметим, что граф 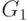 имеет
столько же
вершин, сколько исходный граф, но у него больше ребер. Поэтому рекурсия
в конечном счете приводит к полным графам, для которых задача о раскраске
решается тривиально.
имеет
столько же
вершин, сколько исходный граф, но у него больше ребер. Поэтому рекурсия
в конечном счете приводит к полным графам, для которых задача о раскраске
решается тривиально.
Раскраска ребер
Наряду с задачей о раскраске вершин имеется задача о раскраске ребер
графа, когда цвета назначаются ребрам. Раскраска ребер (или реберная
раскраска) называется правильной, если любые два ребра, имеющие общую
вершину, окрашены в разные цвета. Минимальное число цветов, необходимое
для правильной раскраски ребер графа  , называется хроматическим
индексом графа и обозначается
через
, называется хроматическим
индексом графа и обозначается
через  .
.
Обозначим через 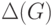 максимальную степень вершины в
графе.
При правильной реберной раскраске все ребра, инцидентные одной вершине,
должны иметь разные цвета. Отсюда следует, что для любого графа выполняется
неравенство
максимальную степень вершины в
графе.
При правильной реберной раскраске все ребра, инцидентные одной вершине,
должны иметь разные цвета. Отсюда следует, что для любого графа выполняется
неравенство 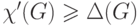 . Для некоторых графов имеет
место строгое неравенство, например,
. Для некоторых графов имеет
место строгое неравенство, например, 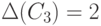 ,
а
,
а 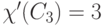 . Следующая теорема, доказанная В.Г.Визингом
в 1964 г.,
показывает, что
. Следующая теорема, доказанная В.Г.Визингом
в 1964 г.,
показывает, что  может отличаться
от
может отличаться
от  не более чем на 1.
не более чем на 1.

