|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Маршруты, связность, расстояния
Маршруты, пути, циклы
Маршрут в графе - это
последовательность
вершин  , такая, что для
каждого
, такая, что для
каждого 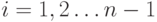 вершины
вершины 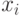 и
и 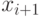 соединены
ребром. Эти
соединены
ребром. Эти 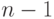 ребер называются ребрами маршрута.
Говорят, что маршрут проходит
через них, а число
ребер называются ребрами маршрута.
Говорят, что маршрут проходит
через них, а число 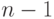 называют длиной маршрута. Говорят,
что маршрут соединяет
вершины
называют длиной маршрута. Говорят,
что маршрут соединяет
вершины 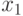 и
и 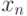 , они называются
соответственно началом и концом маршрута,
вершины
, они называются
соответственно началом и концом маршрута,
вершины 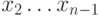 называются промежуточными.
Маршрут называется замкнутым,
если
называются промежуточными.
Маршрут называется замкнутым,
если  .
.
Путь - это маршрут, в котором все ребра различны. Путь называется простым, если и все вершины в нем различны.
Цикл - это замкнутый путь.
Цикл  называется простым, если все
вершины
называется простым, если все
вершины  попарно различны.
попарно различны.
В графе на рисунке 2.1 последовательность вершин
-
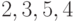 - не маршрут;
- не маршрут; -
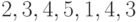 - маршрут, но не путь;
- маршрут, но не путь; -
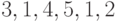 - путь, но не простой;
- путь, но не простой; -
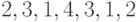 - замкнутый маршрут, но не цикл;
- замкнутый маршрут, но не цикл; -
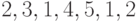 - цикл, но не простой;
- цикл, но не простой; -
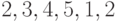 - простой цикл.
- простой цикл.
Установим некоторые простые свойства маршрутов.
Теорема 1. В любом маршруте, соединяющем две различные вершины, содержится простой путь, соединяющий те же вершины. В любом цикле, проходящем через некоторое ребро, содержится простой цикл, проходящий через это ребро.
Доказательство.
Пусть  - маршрут.
Если все его вершины различны, то это уже простой путь. В противном
случае, пусть
- маршрут.
Если все его вершины различны, то это уже простой путь. В противном
случае, пусть  ,
,  . Тогда
последовательность
. Тогда
последовательность 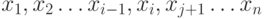 ,
полученная из этого маршрута удалением отрезка
последовательности от
,
полученная из этого маршрута удалением отрезка
последовательности от 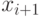 до
до  , тоже
является
маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину.
Продолжая действовать таким образом, после конечного числа
"спрямлений"
получим простой путь, соединяющий
, тоже
является
маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину.
Продолжая действовать таким образом, после конечного числа
"спрямлений"
получим простой путь, соединяющий 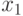 и
и 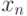 .
Второе утверждение теоремы доказывается аналогично.
.
Второе утверждение теоремы доказывается аналогично.
Отметим, что в формулировке теоремы 1 нельзя заменить слово
"цикл" словами
"замкнутый маршрут". Действительно, если 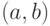 - ребро
графа, то последовательность
- ребро
графа, то последовательность 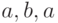 - замкнутый маршрут,
проходящий
через это ребро, но никакого цикла в нем нет.
- замкнутый маршрут,
проходящий
через это ребро, но никакого цикла в нем нет.
Теорема 2. Если в графе степень каждой вершины не меньше  , то в нем есть цикл.
, то в нем есть цикл.
Доказательство.
Найдем в графе простой путь наибольшей длины. Пусть
это 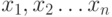 . Вершина
. Вершина 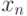 смежна
с
смежна
с 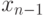 , а так как ее степень не меньше двух, то она смежна еще
хотя
бы с одной вершиной, скажем, с
, а так как ее степень не меньше двух, то она смежна еще
хотя
бы с одной вершиной, скажем, с  . Если бы
. Если бы  была
отлична от
всех вершин пути, то последовательность
была
отлична от
всех вершин пути, то последовательность 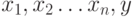 была бы простым путем большей длины. Следовательно,
была бы простым путем большей длины. Следовательно,  - это
одна из вершин пути,
- это
одна из вершин пути, 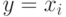 , причем
, причем 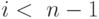 . Но тогда
. Но тогда 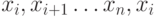 - цикл.
- цикл.

