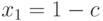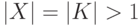НОУ ИНТУИТ | Введение в алгебру. Лекция 7: Системы линейных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать программу

Аннотация: В данной лекции рассматриваются системы линейных уравнений. Рассматриваются методы их решения, приведены основные определения, рассмотрены элементарные преобразования систем, условия их совместности. Рассмотрен ряд характерных задач, доказаны основные теоремы, а также приведены задачи для самостоятельного рассмотрения

Ключевые слова: операции, обратный, поле, таблица, коэффициентами системы, матрица, расширенная матрица, система линейных уравнений, Побочная диагональ, система линейных уравнений однородная, решение системы линейных уравнений, система линейных уравнений несовместная, система линейных уравнений совместная, система линейных уравнений определенная, неопределенной

Системы линейных уравнений

В средней школе рассматривались линейные уравнения ax=b и системы линейных уравнений

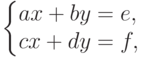
$\left\{ \begin{array}{@{}l@{}} ax+by=e,\\ cx+dy=f, \end{array} \right.$

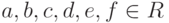где $a, b, c, d, e, f \in R$ - действительные числа.

В излагаемой теории систем линейных уравнений мы будем совершать с коэффициентами операции сложения и умножения, а также делить (т. е. умножать на обратный элемент) на ненулевой элемент. Таким образом, естественно рассматривать системы линейных уравнений с коэффициентами из произвольного поля K. Для понимания основных моментов теории систем линейных уравнений можно считать, что K - поле R действительных чисел.

Наша ближайшая цель - исследовать системы m линейных уравнений общего вида от n переменных x₁, x₂, x₃,...,x_n

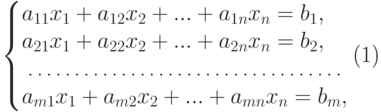$\begin{equation}\label{eq1.1} \left\{ \begin{array}{@{}l@{}} a_{11}x_1+a_{12}x_2+...+a_{1n}x_n=b_1,\\ a_{21}x_1+a_{22}x_2+...+a_{2n}x_n=b_2,\\ \dotfill\\ a_{m1}x_1+a_{m2}x_2+...+a_{mn}x_n=b_m, \end{array} \right. \end{equation}$

( 3.1)

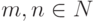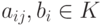где $m,n \in N$ , $a_{ij},b_i \in K$ .

Таким образом, i -е уравнение, $1\le i \le m$ , нашей системы записывается в виде a_i1x₁+a_i2x₂+ ... +a_inx_n=b_i ( a_ij - коэффициент при переменной x_j в i -м уравнении, b_i - свободный член i -го уравнения), или, кратко,

$\sum_{j=1}^n a_{ij}x_j=b_i.$

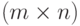Прямоугольная $(m \times n)$ - таблица коэффициентов 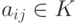$a_{ij} \in K$ ( m строк, n столбцов)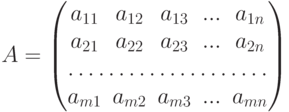

$A= \begin{pmatrix} a_{11}& a_{12}& a_{13} &... &a_{1n}\\ a_{21}& a_{22}& a_{23} &... &a_{2n}\\ \hdotsfor{5}\\ a_{m1}& a_{m2}& a_{m3} &... &a_{mn} \end{pmatrix}$

называется матрицей коэффициентов системы линейных уравнений (3.1), а прямоугольная $(m \times (n+1))$ -матрица ( m строк, n+1 столбец)

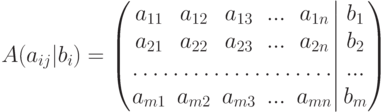
$A(a_{ij}|b_i)= \left(\left. \begin{matrix} a_{11} &a_{12} &a_{13} &... &a_{1n}\\ a_{21} &a_{22} &a_{23} &... &a_{2n}\\ \hdotsfor{5}\\ a_{m1} &a_{m2} &a_{m3} &... &a_{mn} \end{matrix} \right| \begin{matrix} b_1\\ b_2\\ ...\\ b_m \end{matrix} \right)$

называется расширенной матрицей системы линейных уравнений (3.1) (уже полностью ее определяющей).

Если m=n (число уравнений равно числу переменных), то система линейных уравнений (и матрица 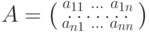$A=\left( \begin{smallmatrix} a_{11}&... & a_{1n}\\ \multispan{3}{\dotfill}\\ a_{n1}&... & a_{nn} \end{smallmatrix}\right)$ ее коэффициентов при переменных) называется квадратной.

В квадратной матрице

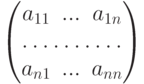
$\begin{pmatrix} a_{11}& ... &a_{1n}\\ \hdotsfor{3}\\ a_{n1}& ... &a_{nn} \end{pmatrix}$

можно определить диагональ и побочную диагональ:

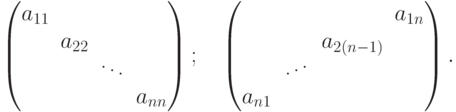
$\begin{pmatrix} a_{11}\\ &a_{22}\\ &&\ddots\\ &&&a_{nn} \end{pmatrix}; \quad \begin{pmatrix} \phantom{a_{11}}&&&a_{1n}\\ &\phantom{a_{22}}&a_{2(n-1)}\\ &\revddots&&\phantom{\ddots}\\ a_{n1}&&\phantom{a_{nn}} \end{pmatrix}.$

Если в системе линейных уравнений b₁=...=b_m=0, то система называется однородной .

Совокупность решений системы линейных уравнений

Определение 3.1.1. Решением системы линейных уравнений (3.1) называется строчка n элементов поля K (l₁,...,l_n), 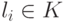$l_i \in K$ , такая, что при подстановке в i -е уравнение, $1\leq i \leq m$ , l₁ вместо x₁, l₂ вместо x₂,...,l_i вместо x_i,...,l_n вместо x_n получаем b_i (свободный член i -го уравнения), т. е.

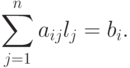
$\sum_{j=1}^{n} a_{ij}l_j=b_i.$

Таким образом, строчка (l₁, ..., l_n) является решением, если значения l₁, ..., l_n соответственно для x₁, ..., x_n удовлетворяют всем m уравнениям системы (3.1).

Через X обозначим совокупность всех решений системы линейных уравнений (3.1).

Замечание 3.1.2.

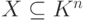$X \subseteq K^n$ (т. е. совокупность всех решений является подмножеством в множестве Kⁿ всех строк длины n элементов из поля K ).
Возможно, что $X=\varnothing$ (т. е. система линейных уравнений не имеет решений), в этом случае система называется несовместной .
Если 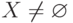$X\ne\varnothing$ (т. е. система имеет решение), то система (3.1) называется совместной . Например, однородная система линейных уравнений всегда имеет нулевое решение, $(0,...,0)\in X\subseteq K^n$ .

Если система имеет только одно решение ( |X|=1 ), то система называется определенной . Если |X| > 1, то совместная система называется неопределенной . Итак, для числа решений имеются следующие возможности:

Число решений
0	1	>1
Система несовместная, $X=\varnothing$	Система определенная, \|X\|=1	Система неопределенная, \|X\|>1
Примеры
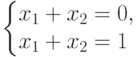$\left\{ \begin{array}{@{}l@{}} x_1+x_2=0,\\ x_1+x_2=1 \end{array} \right$ . $X=\varnothing$ несовместная с. л. у.	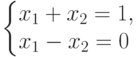$\left\{ \begin{array}{@{}l@{}} x_1+x_2=1,\\ x_1-x_2=0 \end{array} \right$ . $X=\left\{\left(\frac{1}{2},\frac{1}{2}\right)\right\}$ определенная с. л. у.	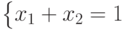$\left\{ \begin{array}{@{}l@{}} x_1+x_2=1 \end{array} \right$ . $x_2=c\in K$ , $X=\{ (1-c,c)\mid\allowbreak c \in K \}$ неопределенная с. л. у.

Основная задача исследования систем линейных уравнений (3.1) заключается в описании (нахождении) множества решений 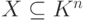$X \subseteq K^n$ (в частности, определения, к какому типу принадлежит система (3.1): несовместная, определенная, неопределенная).

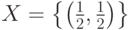
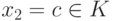Дальше >>

Введение в алгебру

Введение в алгебру

Системы линейных уравнений

Системы линейных уравнений

Совокупность решений системы линейных уравнений

Вопросы и ответы

Студенты

Авторизоваться

Введение в алгебру

Введение в алгебру

Системы линейных уравнений

Системы линейных уравнений

Совокупность решений системы линейных уравнений

Вопросы и ответы

Студенты