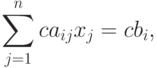Системы линейных уравнений
Эквивалентные системы линейных уравнений
Две системы линейных уравнений от одного набора x1,..., xn неизвестных и соответственно из m и p уравнений
![\begin{alignat*}{2} & (\textbf{I}) &&
\left\{
\begin{array}{@{}l@{}}
a_{11}x_1+...+a_{1n}x_n=b_1,\\
\dotfill\\
a_{m1}x_1+...+a_{mn}x_n=b_m,
\end{array}
\right.\\[2mm] & (\textbf{II}) &\quad & \left\{
\begin{array}{@{}l@{}}
a'_{11}x_1+...+a'_{1n}x_n=b'_1,\\
\dotfill\\
a'_{p1}x_1+...+a'_{pn}x_n=b'_p
\end{array}
\right.
\end{alignat*}](/sites/default/files/tex_cache/ed8f9f44f8e72150021108c81fdd45b4.png)
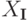 и
и  совпадают (т. е. подмножества
совпадают (т. е. подмножества 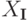 и
и  в Kn совпадают,
в Kn совпадают, 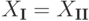 ). Это означает, что: либо они одновременно являются пустыми подмножествами
). Это означает, что: либо они одновременно являются пустыми подмножествами 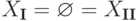 (т. е. обе системы (I) и (II) несовместны), либо они одновременно непустые
(т. е. обе системы (I) и (II) несовместны), либо они одновременно непустые 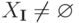 ,
,  и
и 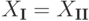 (т. е. каждое решение системы I является решением системы II и каждое решение системы II является решением системы I).
(т. е. каждое решение системы I является решением системы II и каждое решение системы II является решением системы I).Пример 3.2.1.
- Любые две несовместные системы от неизвестных x1,...,xn эквивалентны (в этом случае
 ).
). - Системыэквивалентны (при K= R ), поскольку
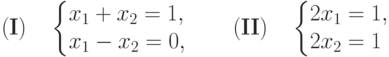
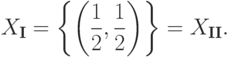
Метод Гаусса
План алгоритма, предложенного Гауссом, был весьма прост:
- применять к системе линейных уравнений последовательно преобразования, не меняющие множество решений (таким образом мы сохраняем множество решений исходной системы), и перейти к эквивалентной системе, имеющей "простой вид" (так называемую ступенчатую форму);
- для "простого вида" системы (со ступенчатой матрицей) описать множество решений, которое совпадает с множеством решений исходной системы.
Отметим, что близкий метод "фан-чен" был известен уже в древнекитайской математике.
Элементарные преобразования систем линейных уравнений (строк матриц)
Определение 3.4.1 (элементарное преобразование 1-го типа). При 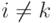 к i -му уравнению системы прибавляется k -е уравнение, умноженное на число
к i -му уравнению системы прибавляется k -е уравнение, умноженное на число 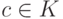 (обозначение: (i)'=(i)+c(k) ; т. е. лишь одно i -е уравнение (i) заменяется на новое уравнение (i)'=(i)+c(k) ). Новое i -е уравнение имеет вид (ai1+cak1)x1+...+(ain+cakn)xn=bi+cbk,
или, кратко,
(обозначение: (i)'=(i)+c(k) ; т. е. лишь одно i -е уравнение (i) заменяется на новое уравнение (i)'=(i)+c(k) ). Новое i -е уравнение имеет вид (ai1+cak1)x1+...+(ain+cakn)xn=bi+cbk,
или, кратко,
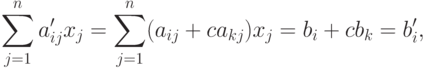
Определение 3.4.2 (элементарное преобразование 2-го типа). При 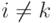 i -е и k -е уравнение меняются местами, остальные уравнения не изменяются (обозначение: (i)'=(k), (k)'=(i) ; для коэффициентов это означает следующее: для j=1,...,n
i -е и k -е уравнение меняются местами, остальные уравнения не изменяются (обозначение: (i)'=(k), (k)'=(i) ; для коэффициентов это означает следующее: для j=1,...,n

Замечание 3.4.3. Для удобства в конкретных вычислениях можно применять элементарное преобразование 3-го типа: i -е уравнение умножается на ненулевое число  , (i)'=c(i).
, (i)'=c(i).
Предложение 3.4.4. Если от системы I мы перешли к системе II при помощи конечного числа элементарных преобразований 1-го и 2-го типа, то от системы II можно вернуться к системе I также элементарными преобразованиями 1-го и 2-го типа.
Доказательство.
- Если
 и (i)'=(i)+c(k), то (k)'=(k), (i)=(i)'-c(k)=(i)'-c(k)'.
и (i)'=(i)+c(k), то (k)'=(k), (i)=(i)'-c(k)=(i)'-c(k)'. - Если
 и (i)'=(k), (k)'=(i), то (i)=(k)', (k)=(i)'.
и (i)'=(k), (k)'=(i), то (i)=(k)', (k)=(i)'.
Замечание 3.4.5. Утверждение верно и с включением в число элементарных преобразований элементарного преобразования 3-го типа. Если  и (i)'=c(i), то
и (i)'=c(i), то 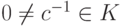 и (i)=c-1(i)'.
и (i)=c-1(i)'.
Теорема 3.4.6.После последовательного применения конечного числа элементарных преобразований 1-го или 2-го типа к системе линейных уравнений получается система линейных уравнений, эквивалентная первоначальной.
Доказательство. Заметим, что достаточно рассмотреть случай перехода от системы I к системе II при помощи одного элементарного преобразования и доказать для множеств решений включение 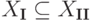 (поскольку в силу доказанного предложения от системы II можно вернуться к системе I и поэтому будем иметь включение
(поскольку в силу доказанного предложения от системы II можно вернуться к системе I и поэтому будем иметь включение 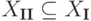 , т. е. будет доказано равенство
, т. е. будет доказано равенство 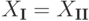 ).
).
Случай 1, элементарное преобразование 1-го типа: (i)'=(i)+c(k),  . Пусть
. Пусть  - решение первой системы. Проверим, что оно удовлетворяет новому i -му уравнению:
- решение первой системы. Проверим, что оно удовлетворяет новому i -му уравнению:
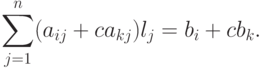
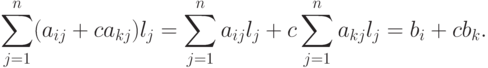
Случай 2, элементарное преобразование 2-го типа: (i)'=(k), (k)'=(i),  . Утверждение очевидно.
. Утверждение очевидно.
Замечание 3.4.7. Утверждение верно и для элементарного преобразования 3-го типа: (i)'=c(i), 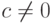 . Действительно, подставляя решение
. Действительно, подставляя решение 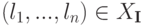 в новое i -е уравнение
в новое i -е уравнение