Поле C комплексных чисел
Понятие числа является одним из основных понятий в математических теориях. К основным числовым системам принадлежат:
- натуральные числа N (полукольцо);
- натуральные числа с нулем
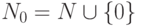 (полукольцо с нулем);
(полукольцо с нулем); - целые числа Z (кольцо);
- рациональные числа Q (поле);
- действительные числа R (поле).
При этом
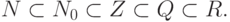
 , называется полем, если:
, называется полем, если:-
операция сложения
- коммутативна (
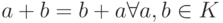 );
); - ассоциативна (
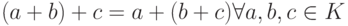 );
); - существует нейтральный элемент 0 (
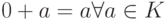 );
); -
 существует противоположный элемент -a ( a+(-a)=0 )
существует противоположный элемент -a ( a+(-a)=0 )
(кратко, (K, +) - коммутативная группа);
- коммутативна (
-
операция умножения
- коммутативна (
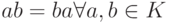 );
); - ассоциативна (
 );
); - существует нейтральный элемент 1 (
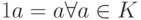 ),
), 
- коммутативна (
-
имеет место дистрибутивность, связывающая операции сложения и умножения (
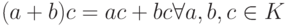 ).
).Условия 1), 2), 3) определяют коммутативное кольцо.
- Имеет место обратимость ненулевых элементов (
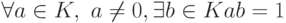 ).
).
Поле действительных чисел R, при всех его достоинствах, не является алгебраически замкнутым полем (т. е. многочлены с действительными коэффициентами могут не иметь действительных корней: например, многочлен x2+1 не имеет действительного корня). Нашей целью является построение расширения C поля действительных чисел R, 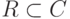 , в котором есть такой элемент
, в котором есть такой элемент 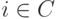 , что i2=-1 (уравнение x2+1=0 имеет решение), при этом в некотором смысле это минимальное расширение с этим свойством. Построенное поле C окажется алгебраически замкнутым (алгебраическим замыканием поля R ).
, что i2=-1 (уравнение x2+1=0 имеет решение), при этом в некотором смысле это минимальное расширение с этим свойством. Построенное поле C окажется алгебраически замкнутым (алгебраическим замыканием поля R ).
Анализ ситуации
Допустим, что существует поле K, содержащее в качестве подполя поле действительных чисел, 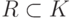 , и элемент
, и элемент 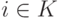 такой, что i2=-1. Тогда:
такой, что i2=-1. Тогда:
- для
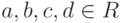 равенство a+bi=c+di выполнено тогда и только тогда, когда a=b, c=d
равенство a+bi=c+di выполнено тогда и только тогда, когда a=b, c=dДоказательство. Если a+bi=c+di, то a-c=(d-b)i, поэтому (a-c)2=-(d-b)2, следовательно, (a-c)2=0=(d-b)2, т. е. a=c, b=d.
- подмножество D всех элементов a+bi,
 , замкнуто относительно операции сложения (a+bi)+(c+di)=(a+c)+(b+d)i,
, замкнуто относительно операции сложения (a+bi)+(c+di)=(a+c)+(b+d)i, 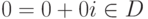 является в D нейтральным элементом, -(a+bi)=(-a)+(-b)i - противоположный элемент для a+bi. Итак, D относительно сложения - коммутативная группа.
является в D нейтральным элементом, -(a+bi)=(-a)+(-b)i - противоположный элемент для a+bi. Итак, D относительно сложения - коммутативная группа. - подмножество D замкнуто относительно умножения (a+bi)(c+di)=(ac-bd)+(ad+bc)i.
- (a+bi)(a-bi)=a2+b2.
- если
 , то a2+b2>0, иследовательно,
, то a2+b2>0, иследовательно,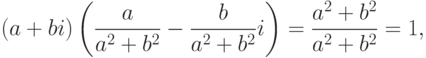 для
для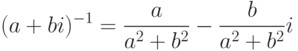
 . Итак, D является подполем поля K,
. Итак, D является подполем поля K,  ,
, 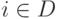 , D - наименьшее подполе в K, содержащее R и i.
, D - наименьшее подполе в K, содержащее R и i.


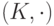 - коммутативный
- коммутативный