Нелиненйые уравнения
Практическое занятие "Решение линейных и нелинейных уравнений"
Цель занятия
Аппробировать базовые численные методы для решения систем линейных алгебраических уравнений и нелинейных трансцендентных уравнений.
Практическая задача
Как мы уже отмечали на лекциях, важнейшим понятием для решения
системы линейных алгебраических уравнений является число
обусловленности матрицы. Вычислим это число для некоторых матриц.
Согласно определению находить это число затруднительно. Однако для
симметричных положительно определенных матриц это число может быть
найдено с помощью собственных значений этой матрицы. Пусть
симметричная положительно определенная матрица  имеет
собственные значения
имеет
собственные значения  , где
, где  - минимальное собственное значение, а
- минимальное собственное значение, а  -
максимальное собственное значение. Тогда число обусловленности
этой матрицы можно вычислить по формуле
-
максимальное собственное значение. Тогда число обусловленности
этой матрицы можно вычислить по формуле
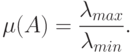
Рассмотрим матрицу
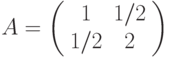
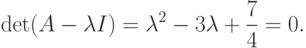
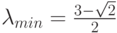 ,
,  . Число обусловленности этой
матрицы равно
. Число обусловленности этой
матрицы равно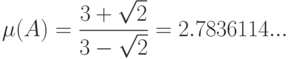
Рассмотрим применение метода Холецкого для этой матрицы. Напомним,
что метод Холецкого позволяет найти такую матрицу  , которая
имеет вид
, которая
имеет вид
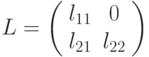
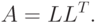
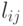 находятся
следующим образом
находятся
следующим образом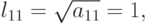
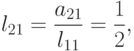

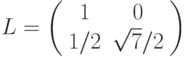
Теперь рассмотрим практические вопросы реализации метода Ньютона для нахождения решений трансцендентных уравнений. Напомним, что метод Ньютона применим для решения уравнений вида
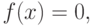
 - непрерывно дифференцируемая функция. Основной
вопрос, который здесь возникает, состоит в том, чтобы быть
уверенным в сходимости итераций Ньютона. Основным достаточным
условием сходимости итераций Ньютона является выполнение
неравенства
- непрерывно дифференцируемая функция. Основной
вопрос, который здесь возникает, состоит в том, чтобы быть
уверенным в сходимости итераций Ньютона. Основным достаточным
условием сходимости итераций Ньютона является выполнение
неравенства
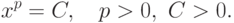
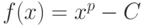 . Производная этой
функции имеет вид
. Производная этой
функции имеет вид  . Тогда имеем неравенство
. Тогда имеем неравенство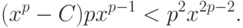
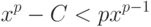
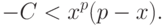
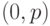 метод Ньютона сходится.
метод Ньютона сходится.