Научное программирование
Практическое занятие "Вычислительные процедуры"
Цель занятия
Продемонстрировать на практике различные вычислительные процедуры. Научится самостоятельно реализовывать вычислительные процедуры для решения задач численного анализа.
Практическая задача
Рассмотрим простую задачу вычисления факториала числа.
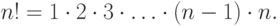
Первая вычислительная процедура выглядит следующим образом:
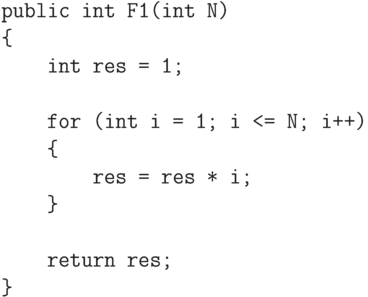
Вторая процедура будет основана на рекурсивном вызове:

С математической точки зрения - обе эти процедуры эквивалентны, но с вычислительной точки зрения между этими реализациями есть существенные различия. Чтобы оценить быстродействие наших процедур выполним следующий тест:
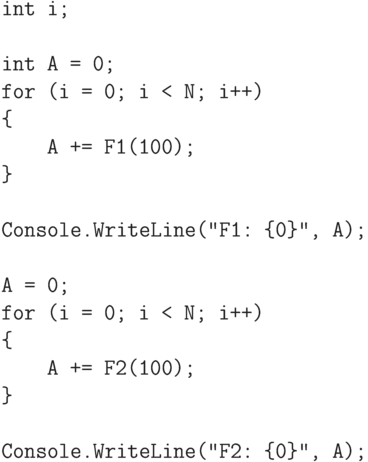
Заметим, что кроме быстродействия необходимо рассматривать также и такой параметр, как требуемая память. Для рекурсивных процедур с большим уровнем вложения может потребоваться большой объем стека.
В лекции, посвященной вычислительным процедурам, мы отмечали, что
из-за наличия машинного  эквивалентные (с математической
точки зрения) вычислительные процедуры могут давать различные
результаты. В качестве примера - попробуем проверитЬ на
компьютере выполнение различных тождеств:
эквивалентные (с математической
точки зрения) вычислительные процедуры могут давать различные
результаты. В качестве примера - попробуем проверитЬ на
компьютере выполнение различных тождеств:

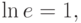
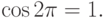

В качестве демонстрации свойства устойчивости и неустойчивости различных вычислительных процедур. Рассмотрим одну задачу, которая имеет известное решение. Задача - найти значение решения дифференциального уравнения
 |
( 1) |
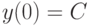 |
( 2) |
 .
.Известно, что решением задачи 1 - 2 будет
число  . Если мы будем решать эту задачу с помощью
численного метода, например, метода Эйлера, то устойчивость нашей
вычислительной процедуры будет зависеть от знака числа
. Если мы будем решать эту задачу с помощью
численного метода, например, метода Эйлера, то устойчивость нашей
вычислительной процедуры будет зависеть от знака числа  . Если
. Если 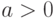 , то наша вычислительная процедура является неустойчивой.
, то наша вычислительная процедура является неустойчивой.
