Принципы организации вычислительных процедур
Обратимся к способам построения операторов ![T[n]](/sites/default/files/tex_cache/89d78b9b3c515aec339191d632e54cb4.png) . Мы рассмотрим
два принципиальных метода построения приближенных решений.
Во-первых, это метод дискретизации. Как правило, пространство
. Мы рассмотрим
два принципиальных метода построения приближенных решений.
Во-первых, это метод дискретизации. Как правило, пространство  состоит из бесконечного числа элементов, более того, часто это
пространство является бесконечномерным линейным пространством. А
на компьютере мы можем работать только с конечными множествами.
Поэтому для каждого целого
состоит из бесконечного числа элементов, более того, часто это
пространство является бесконечномерным линейным пространством. А
на компьютере мы можем работать только с конечными множествами.
Поэтому для каждого целого  вводится конечное множество
вводится конечное множество 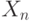 и
два отображения:
и
два отображения:

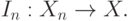
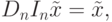
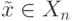 .
.Далее решается следующая задача
![A[I_n(x)]=y.](/sites/default/files/tex_cache/3e205408c3e6463a648ed874ba5cef47.png) |
( 5.2) |
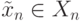 ,
тогда оператор
,
тогда оператор  строится по формуле:
строится по формуле:![T[n]=I_n\tilde x_n.](/sites/default/files/tex_cache/cd9790e03276aebb0c83e915440fca06.png)
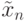 осуществляется из конечного
множества, то такой выбор может быть осуществлен для заданного
осуществляется из конечного
множества, то такой выбор может быть осуществлен для заданного  на вычислительной машине.
на вычислительной машине.Вычислительные процедуры, основанные на методе дискретизации пространства, как правило, применяются для нахождения приближенных решений дифференциальных и интегральных уравнений. В том числе и для приближенного решения уравнений в частных производных.
Другим часто применяемым принципом построения вычислительных
процедур является использование принципа неподвижной точки
отображения. Предположим, что решение уравнения 5.1
является неподвижной точкой некоторого другого отображения 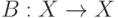 , то есть если
, то есть если 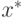 - решение задачи 5.1, то имеет
место:
- решение задачи 5.1, то имеет
место:
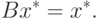 |
( 5.3) |
 имеет единственную неподвижную точку.
имеет единственную неподвижную точку.Во многих случаях для конструктивного нахождения неподвижной точки
оператора  или, соответственно, решения уравнения 5.3
используется метод простых итераций. Пусть задано начальное
приближение
или, соответственно, решения уравнения 5.3
используется метод простых итераций. Пусть задано начальное
приближение 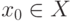 , тогда последующие приближения строятся по
формуле:
, тогда последующие приближения строятся по
формуле:

 является сжимающим отображением, то
оператор
является сжимающим отображением, то
оператор  имеет единственную неподвижную точку и
последовательность
имеет единственную неподвижную точку и
последовательность 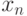 сходится к этой точке при любом выборе
начального приближения.
сходится к этой точке при любом выборе
начального приближения.Напомним, что отображение  называется сжимающим, если
существует такое число
называется сжимающим, если
существует такое число  , что для любых
, что для любых 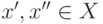 имеет место
имеет место
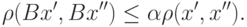
Рассмотрим пример на применение метода неподвижных точек. Пусть
пространства  и
и  являются пространствами
являются пространствами  с
евклидовой метрикой. В качестве оператора
с
евклидовой метрикой. В качестве оператора  возьмем квадратную
матрицу:
возьмем квадратную
матрицу:
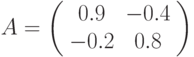
 |
( 5.4) |
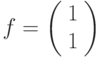 - вектор столбец. Таким образом, уравнение
5.4 представляет собой систему линейных алгебраических
уравнений. Чтобы использовать метод неподвижной точки введем
оператор
- вектор столбец. Таким образом, уравнение
5.4 представляет собой систему линейных алгебраических
уравнений. Чтобы использовать метод неподвижной точки введем
оператор  следующим образом:
следующим образом: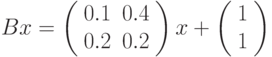
 совпадает с точным
решением уравнения 5.6. Кстати, точное решение этого
уравнения имеет вид:
совпадает с точным
решением уравнения 5.6. Кстати, точное решение этого
уравнения имеет вид: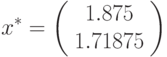

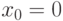 . Знание точного решения позволит нам вычислять
значения
. Знание точного решения позволит нам вычислять
значения 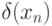 . Приведем программу расчета.
. Приведем программу расчета.


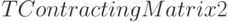 на нашем примере.
на нашем примере.![x_n=[1.000000E+000,1.000000E+000]; d_n=1.132354E+000\\
x_n=[1.500000E+000,1.400000E+000]; d_n=4.921652E-001\\
x_n=[1.710000E+000,1.580000E+000]; d_n=2.155842E-001\\
x_n=[1.803000E+000,1.658000E+000]; d_n=9.420490E-002\\
x_n=[1.843500E+000,1.692200E+000]; d_n=4.119651E-002\\
x_n=[1.861230E+000,1.707140E+000]; d_n=1.801125E-002\\
x_n=[1.868979E+000,1.713674E+000]; d_n=7.875165E-003\\
x_n=[1.872368E+000,1.716531E+000]; d_n=3.443224E-003\\
x_n=[1.873849E+000,1.717780E+000]; d_n=1.505477E-003\\
x_n=[1.874497E+000,1.718326E+000]; d_n=6.582366E-004\\
x_n=[1.874780E+000,1.718564E+000]; d_n=2.877996E-004\\
x_n=[1.874904E+000,1.718669E+000]; d_n=1.258341E-004\\
x_n=[1.874958E+000,1.718715E+000]; d_n=5.501820E-005\\
x_n=[1.874982E+000,1.718734E+000]; d_n=2.405550E-005\\
x_n=[1.874992E+000,1.718743E+000]; d_n=1.051774E-005\\
x_n=[1.874996E+000,1.718747E+000]; d_n=4.598653E-006\\
x_n=[1.874998E+000,1.718749E+000]; d_n=2.010661E-006\\
x_n=[1.874999E+000,1.718749E+000]; d_n=8.791174E-007\\
x_n=[1.875000E+000,1.718750E+000]; d_n=3.843748E-007\\
x_n=[1.875000E+000,1.718750E+000]; d_n=1.680595E-007\\
x_n=[1.875000E+000,1.718750E+000]; d_n=7.348034E-008\\
x_n=[1.875000E+000,1.718750E+000]; d_n=3.212767E-008\\
x_n=[1.875000E+000,1.718750E+000]; d_n=1.404712E-008\\
x_n=[1.875000E+000,1.718750E+000]; d_n=6.141797E-009\\
x_n=[1.875000E+000,1.718750E+000]; d_n=2.685366E-009\\](/sites/default/files/tex_cache/283bbb1c774162e5ab0f45bf67107458.png)
Мы видим, что величина 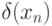 стремится к нулю, а сама
последовательность
стремится к нулю, а сама
последовательность 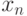 сходится к точному решению.
сходится к точному решению.
Классический подход вычислительной математики состоит в том, что строится некоторая эффективно выполняемая вычислительная процедура позволяющая получать приближенные решения, которые сходятся (в том или ином смысле) к точному решению. Такой подход подразумевает, что исходная задача является корректной. Корректность задачи по Адамару означает выполнения следующих трех условий:
- Существование решения
- Единственность решения
- Непрерывная зависимость решения от оператора задач, правой части, начального условия
В начале прошлого века могло показаться, что эти условия всегда должны быть выполнены для имеющих физический смысл задач. Однако довольно быстро выяснилось, что наука и техника предъявляют большой класс задач, для которых условия некоторые из условий 1--3 не выполнены. К таким задачам относятся уравнения Фредгольма первого рода, обратные задачи для дифференциальных уравнений, задачи аналитического продолжения функций и многие другие. Задачи, для которых не выполнены какие-либо из условий 1--3, называются некорректными задачами. Некорректные задачи возникают в физике, например, неустойчивость Релея-Тейлора.
Как правило, применять классические вычислительные процедуры для решения некорректных задач не удается. В середине XX-го века известным математиком А.Н.Тихоновым были заложены основы теории регуляризации некорректных задач. Эти результаты нашли свое эффективное применение во многих научно-технических областях.
Изучение теории регуляризации некорректных задач выходит за рамки нашего курса.
Ключевые термины
Корректность задачи по Адамару - существование единственного решения у задачи и непрерывная зависимость решения от данных задачи.
Невязка приближенного решения - количественная мера неудовлетворения приближенным решением уравнению.
Операторное уравнение - уравнение в абстрактных пространства записанное с помощью операторов в этих пространствах.
Принцип неподвижной точки отображение - существование такого элемента для оператора, который отображается этим оператором в себя.
Краткие итоги: Рассмотрены различные способы организации вычислительных процедур для решения операторных уравнений. Рассмотрены вопросы связи невязки и точности решений. Приведен пример организации итерационной процедуры.
