|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Сети очередей
Многомерные сети очередей
В этой секции мы рассматриваем сети очередей с более чем одним типом клиентов. Клиенты одного и того же типа принадлежат заданному классу или цепочке. В Лекции 10 мы рассматривали системы с потерями, обслуживающие несколько типов клиентов (услуг), и замечали, что может быть получена мультипликативная форма и может быть применен алгоритм свертывания.
M/M/1 -система организации очереди с одним обслуживающим прибором
Pис.14.7 иллюстрирует систему организации очереди с одним обслуживающим прибором и с 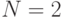 типа заявок от клиентов (цепочек). Заявки от клиентов прибывают в систему согласно Пуассоновскому потоку вызовов с интенсивностью
типа заявок от клиентов (цепочек). Заявки от клиентов прибывают в систему согласно Пуассоновскому потоку вызовов с интенсивностью  . Состояние
. Состояние  определено как состояние
определено как состояние  заявок клиента типа 1 и
заявок клиента типа 1 и  заявок от клиента типа 2. Интенсивность обслуживания
заявок от клиента типа 2. Интенсивность обслуживания 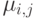 в состоянии
в состоянии  может быть выбрана зависящей от состояния, например:
может быть выбрана зависящей от состояния, например:
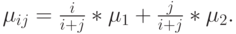
Интенсивности обслуживания могут интерпретироваться несколькими способами, но они должны соответствовать симметричной системе организации очереди при наличии одного обслуживающего прибора.
Одна из интерпретаций соответствует совместному использованию процессора, то есть все  клиентов совместно используют обслуживающий прибор, а производительность сервера является постоянной. Зависимость состояния от типа клиента происходит из-за разности в интенсивности обслуживания двух типов клиентов. То есть число заявок от клиентов, покидающих систему, в единицу времени зависит от типа клиентов, обслуживаемых в настоящее время.
клиентов совместно используют обслуживающий прибор, а производительность сервера является постоянной. Зависимость состояния от типа клиента происходит из-за разности в интенсивности обслуживания двух типов клиентов. То есть число заявок от клиентов, покидающих систему, в единицу времени зависит от типа клиентов, обслуживаемых в настоящее время.
Можно показать, что обслуживаемая заявка с вероятностью 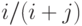 принадлежит к типу 1 и с вероятностью
принадлежит к типу 1 и с вероятностью  - к типу 2 независимо от дисциплины обслуживания.
- к типу 2 независимо от дисциплины обслуживания.
Pис.14.8 дает часть диаграммы переходов состояний. Диаграмма обратима, так как поток по часовой стрелке равняется потоку против часовой стрелки. Следовательно, есть местное равновесие, и все вероятности состояния могут быть выражены с помощью  :
:
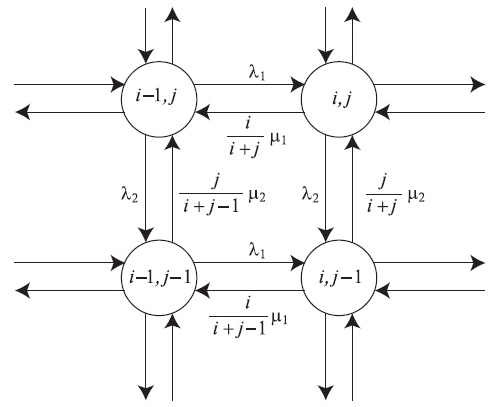
Рис. 14.8. Диаграмма переходов состояний для многомерной системы M/M/1 с совместным использованием процессора.
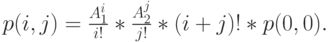 |
( 14.14) |
Используя нормализацию, получаем  :
:

По сравнению с многомерной B-формулой Эрланга, здесь существует дополнительный коэффициент  !. Мультипликативная форма выражения между цепочками (на узле) потеряна, но мультипликативная форма между узлами все еще поддерживается.
!. Мультипликативная форма выражения между цепочками (на узле) потеряна, но мультипликативная форма между узлами все еще поддерживается.
Примем, что есть  различных типов клиентов (цепочек) вероятности состояния для единственного узла, и получаем:
различных типов клиентов (цепочек) вероятности состояния для единственного узла, и получаем:
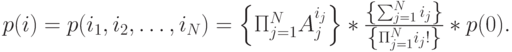 |
( 14.15) |
Это может быть выражено полиномиальным распределением (4.37):
 |
( 14.16) |
Для бесконечного числа мест ожидания вероятности состояния общего количества клиентов:
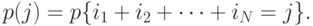
Если 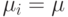 , то система идентична
, то система идентична 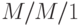 - системе с интенсивностью поступления
- системе с интенсивностью поступления 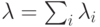 :
:
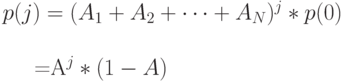
Чтобы получить этот результат, используется биноминальное разложение. Диаграмма переходов состояний на рис.14.8 может также интерпретироваться как диаграмма переходов состояний системы M/G/1-LCFS-PR (приоритетное возвращение к работе). Очевидно, что M/G/1-LCFS-PR обратимо, потому что процесс в диаграмме переходов состояний проходит одинаково как вперед из нуля, так и назад, чтобы вернуться в нуль.
Можно показать, что диаграмма переходов состояний нечувствительна к распределению времени обслуживания, так что она справедлива для системы организации очереди  . Pис.14.8 соответствует диаграмме переходов состояний для системы организации очереди с одним обслуживающим прибором и гиперэкспоненциально распределенными временами обслуживания (см. (10.7)), например.
. Pис.14.8 соответствует диаграмме переходов состояний для системы организации очереди с одним обслуживающим прибором и гиперэкспоненциально распределенными временами обслуживания (см. (10.7)), например. 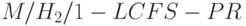 или
или  .
.
Заметим, что для 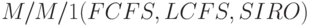 необходимо, чтобы все клиенты имели одно и то же среднее время обслуживания, которое должно быть экспоненциально распределенным. Другими словами, обслуживаемый клиент не будет случайным клиентом среди
необходимо, чтобы все клиенты имели одно и то же среднее время обслуживания, которое должно быть экспоненциально распределенным. Другими словами, обслуживаемый клиент не будет случайным клиентом среди  клиентов в системе.
клиентов в системе.
В заключение заметим, что системы организации очереди c одним обслуживающим прибором и большим количеством типов клиентов будут иметь мультипликативную форму только тогда, когда узел имеет симметричную систему организации очереди:  или
или 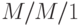 с одним и тем же временем обслуживания для всех клиентов.
с одним и тем же временем обслуживания для всех клиентов.
М/М/п система организации очереди
Мы можем также получить рассмотренные выше результаты для системы с  обслуживающими приборами. Для
обслуживающими приборами. Для 
получаем ту же самую вероятность относительного состояния, что и для многоразмерной B-формулы Эрланга. Для  получаем решение только для простого случая, когда
получаем решение только для простого случая, когда 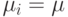 то есть когда все типы (цепочки) клиентов имеют одно и то же среднее время пребывания в системе. Мы тогда находим вероятности состояния, данные в (10.9), и система имеет мультипликативную форму.
то есть когда все типы (цепочки) клиентов имеют одно и то же среднее время пребывания в системе. Мы тогда находим вероятности состояния, данные в (10.9), и система имеет мультипликативную форму. 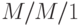 можно рассматривать как частный случай
можно рассматривать как частный случай 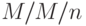 и по аналогии с системами с потерями (Лекция 12).
и по аналогии с системами с потерями (Лекция 12).
Закрытые сети очередей с несколькими цепочками
Рассмотрение сетей очередей, имеющих много цепочек, аналогично случаю с единственной цепочкой. Основное различие состоит в том, что классическая формула и алгоритмы заменены соответствующей многомерной формулой.
Алгоритм свертывания
Алгоритм по существу такой же, как и в случае единственной цепочки.
Шаг 1. Рассмотрим каждую цепочку так, как будто она является единственной в сети. Найдите относительную нагрузку в каждом узле, решая уравнения равновесия потока (14.5). В произвольном опорном узле принимаем, что нагрузка равна единице. Для каждой цепочки мы можем выбрать в качестве опорного узла свой узел. Для цепочки  в узле
в узле  относительная интенсивность прибытия
относительная интенсивность прибытия  (используем верхний индекс, чтобы указать номер цепочки) получается из:
(используем верхний индекс, чтобы указать номер цепочки) получается из:
 |
( 14.17) |
где:
 - число узлов,
- число узлов,
 - число цепочек,
- число цепочек,
 - вероятность, что клиент цепочки
- вероятность, что клиент цепочки  перейдет с узла
перейдет с узла  к узлу
к узлу  .
.
Мы выбираем произвольный узел как опорный узел, например узел 1, то есть  . Относительная нагрузка в узле
. Относительная нагрузка в узле  клиентов цепочки
клиентов цепочки  тогда:
тогда:

где  - среднее время обслуживания в узле
- среднее время обслуживания в узле  для клиентов цепочки
для клиентов цепочки  . Обратите внимание, что j - индекс, а не степень.
. Обратите внимание, что j - индекс, а не степень.
Шаг 2. На основе значений относительных нагрузок, найденных на шаге 1, мы получаем многомерные вероятности состояния для каждого узла. Каждый узел рассматривается отдельно. Далее, усекаем пространство состояний согласно числу клиентов в каждой цепочке. Например, для узла 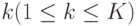 :
:

где 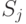 - число заявок от клиентов в цепочке
- число заявок от клиентов в цепочке  .
.
Шаг 3. Чтобы найти вероятности состояния полной сети, сверты ваем вероятности состояния каждого узла подобно случаю единственной цепочки, - разница в том, что в данном случае свертывание многомерно. Когда выполним последнее свертывание, получим критерии качества работы последнего узла. Снова изменяя порядок узлов, мы можем получить критерии качества работы всех узлов.
Общее количество состояний увеличивается быстро. Например, если цепочка  имеет
имеет  заявок клиентов, то общее количество состояния в каждом узле становится:
заявок клиентов, то общее количество состояния в каждом узле становится:

Пути  цепей с
цепей с 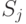 заявками в цепи
заявками в цепи  могут быть распределены в сети очередей с
могут быть распределены в сети очередей с  узлами:
узлами:
 |
( 14.18) |
где  - номер узлов, посещенных клиентом в цепи
- номер узлов, посещенных клиентом в цепи  , и:
, и:
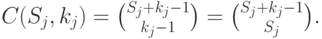 |
( 14.19) |
Алгоритм лучше всего проиллюстрировать примером.
Пример 14.7.1: Модель Пальма восстановления машин с двумя типами клиентов
Уже отмечалось в Примере 14.4.1, что эта система может быть смоделирована как сеть очередей с двумя узлами.
Узел 1 соответствует терминалам (машинам), в то время как узел 2 - центральному процессору (ремонтником). Узел 2 - система с одним обслуживающим прибором, тогда как узел 1 смоделирован как система с бесконечным числом обслуживающих приборов. Число клиентов в цепочках - (  ) и среднее время обслуживания в узле
) и среднее время обслуживания в узле 
Относительная нагрузка цепочки 1 обозначена 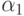 в узле 1 и
в узле 1 и 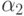 в узле 2. Точно так же нагрузка в цепочке 2 обозначена
в узле 2. Точно так же нагрузка в цепочке 2 обозначена 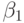 и соответственно
и соответственно 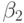 . Применяя алгоритм свертывания, получаем:
. Применяя алгоритм свертывания, получаем:
Шаг 1.
Цепочка 1: 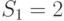 клиента
клиента
Относительная нагрузка:  .
.
Цепочка 2: 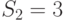 клиента
клиента
Относительная нагрузка: 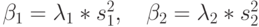 .
.
Шаг 2.
Для узла 1 ( IS ) вероятность относительного состояния (см10.9):

Для узла 2 (обслуживающий прибор) (см.14.15) мы имеем:
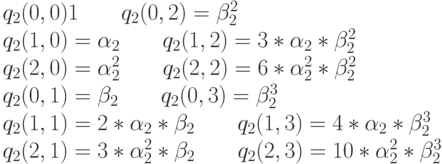
Шаг 3.
Затем мы делаем свертку. Мы знаем, что общее количество клиентов - (2,3), то есть нас интересуют только состояния (2, 3):
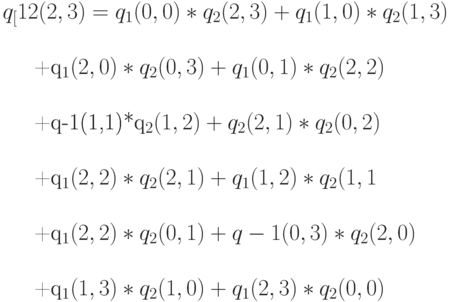
Использование полученных значений дает:
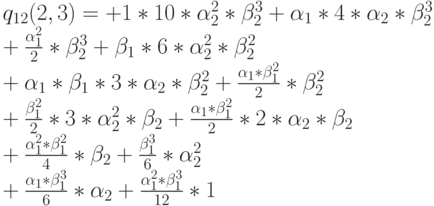
Обратите внимание, что 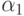 и
и 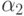 (цепочка 1) появляются во второй степени, тогда как
(цепочка 1) появляются во второй степени, тогда как 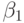 и
и 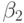 (цепочка 2) - в третьей степени, что соответствует числу клиентов в каждой цепочке. Из-за этого существенны только относительные нагрузки, а абсолютные вероятности получают нормализацией, делением всех элементов
(цепочка 2) - в третьей степени, что соответствует числу клиентов в каждой цепочке. Из-за этого существенны только относительные нагрузки, а абсолютные вероятности получают нормализацией, делением всех элементов 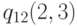 . Теперь достаточно просто получить детальные вероятности состояния. Только в состоянии с элементами
. Теперь достаточно просто получить детальные вероятности состояния. Только в состоянии с элементами  центральный процессор (ремонтник) свободен. Если два типа клиентов идентичны, модель упрощается и сводится к модели Пальма восстановления машин с 5-ю терминалами.
центральный процессор (ремонтник) свободен. Если два типа клиентов идентичны, модель упрощается и сводится к модели Пальма восстановления машин с 5-ю терминалами.
В этом случае мы имеем:
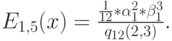
Выбирая, 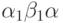 и
и 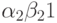 , получаем:
, получаем:

то есть, как и ожидалось, B- формулу Эрланга.

