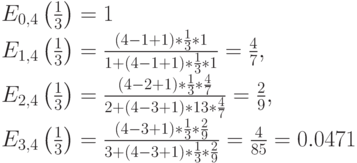|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Полнодоступные системы с потерями
Распределение Энгсета
Единственная разница по сравнению с материалами секции 8.2 - то, что число источников S теперь больше или равно числу пучков каналов (каналам), 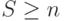 . Поэтому, попытки вызова могут быть потеряны.
. Поэтому, попытки вызова могут быть потеряны.
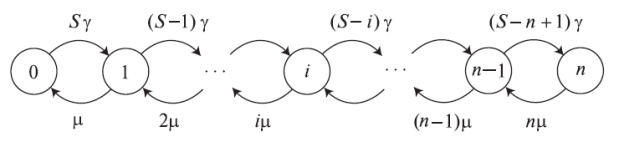
Рис. 8.4. Диаграмма переходов состояний для случая распределения Энгсета с S>n, где S - число источников и n - число каналов.
Вероятности состояния
Уравнения сечения идентичны (8.1), но они существуют только для 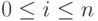 (рис.8.4). Уравнение нормализации (8.2):
(рис.8.4). Уравнение нормализации (8.2):
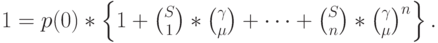
Из него мы получаем p(0) и, подставляя  , получаем вероятности состояния, которые равны:
, получаем вероятности состояния, которые равны:
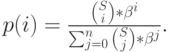 |
( 8.24) |
Тем же самым способом, который мы применяли выше, используя (8.8), мы можем переписать это выражение в форме, которая является аналогом (8.4):
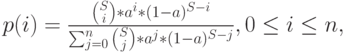 |
( 8.25) |
Характеристики нагрузки в модели Энгсета
Распределение Энгсета сопровождается более сложными вычислениями, чем Эрланговская система с потерями. Основная проблема в том, что нужно понять, как найти критерии качества работы непосредственно из вероятностей состояния, используя определения. Энгсетовская система характеризуется следующими параметрами:  - предложенная нагрузка на свободный источник, S - число источников и n - число каналов.
- предложенная нагрузка на свободный источник, S - число источников и n - число каналов.
Потери по времени Е, по определению, пропорциональны времени блокирования системы для новых попыток вызова, то есть р(n) (8.24):
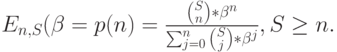 |
( 8.26) |
Потери по вызовам В, по определению, пропорциональны числу потерянных попыток вызова. Блокируются только попытки вызова, достигающие системы в состоянии п. В течение одной единицы времени мы получаем следующее отношение между числом блокированных попыток вызова и общим количеством попыток вызова:
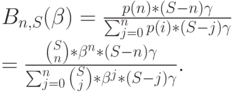
Используя

мы имеем:
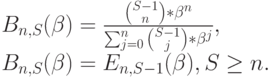 |
( 8.27) |
Этот результат можно интерпретировать следующим образом. Вероятность того, что попытка вызова от случайного источника (абонента) будет отклонена, равна вероятности того, что остальные (S-1) источники заняли все п каналов. Это называется теоремой поступления, и можно показать, что она справедлива для систем с явными потерями и для систем с ожиданием и ограниченным числом источников. Результат основан на вычислении произведения среди источников и свертывании источников. Поскольку Е увеличивается, когда увеличивается S, мы имеем:
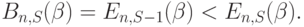
Теорема 8.1. Теорема поступления: Для всех систем с ограниченным числом источников, случайный источник при поступление заявки будет наблюдать состояние системы так, как будто сам источник не принадлежит этой системе.
Свойство PASTA включено в этот случай, потому что бесконечное число источников минус один есть бесконечное число.
Обслуженная нагрузка: применяя уравнение сечения между состоянием [i - 1] и состоянием [i], мы получаем:
 |
( 8.28) |
 |
( 8.29) |
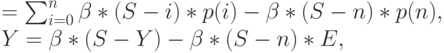 |
( 8.30) |
Поскольку  . Последнее уравнение решается относительно Y:
. Последнее уравнение решается относительно Y:
 |
( 8.31) |
Потери по нагрузке 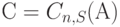 . Это самая важная характеристика потерь. Предложенная нагрузка дается в (8.20), и мы получаем:
. Это самая важная характеристика потерь. Предложенная нагрузка дается в (8.20), и мы получаем:
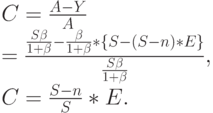 |
( 8.32) |
Мы можем также найти обслуженную нагрузку, если знаем потери по вызовам В. Число попыток принятия вызовов от источника, который находится в свободном состоянии, в среднем 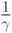 в единицу времени прежде, чем источник сгенерирует одну попытку вызова - 1(1-В), и каждый принятый вызов имеет среднюю продолжительность
в единицу времени прежде, чем источник сгенерирует одну попытку вызова - 1(1-В), и каждый принятый вызов имеет среднюю продолжительность 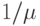 - Таким образом, обслуженная нагрузка на один источник есть соотношение времени: когда источник является занятым, она будет:
- Таким образом, обслуженная нагрузка на один источник есть соотношение времени: когда источник является занятым, она будет:
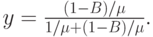
Полная обслуженная нагрузка будет:
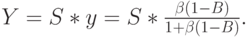 |
( 8.33) |
Приравнивая эти два выражения для обслуженной нагрузки (8.31) и (8.33), мы получаем следующее отношение между Е и В:
 |
( 8.34) |
Число попыток вызова в единицу времени:
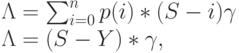 |
( 8.35) |
где Y - обслуженная нагрузка (8.28). Таким образом, из уравнения (S-Y) среднее число свободных источников является очевидным. Исторически, полная предложенная нагрузка была определена как 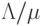 . Это, однако, вводит в заблуждение, потому что мы не можем принять, что каждая повторная попытка вызова имеет среднее время пребывания в системе, равное
. Это, однако, вводит в заблуждение, потому что мы не можем принять, что каждая повторная попытка вызова имеет среднее время пребывания в системе, равное 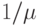 -Также это определение создает большое неудобство, потому что предложенная нагрузка по этому определению зависит от состояния системы (числа занятых каналов). Также возможно, что немногие из доступных обслуживающих много попыток вызова устройств блокированы, а свободные источники с более высоким средним временем поступления вызовов генерируют больше попыток вызова в единицу времени.
-Также это определение создает большое неудобство, потому что предложенная нагрузка по этому определению зависит от состояния системы (числа занятых каналов). Также возможно, что немногие из доступных обслуживающих много попыток вызова устройств блокированы, а свободные источники с более высоким средним временем поступления вызовов генерируют больше попыток вызова в единицу времени.
Потерянная нагрузка:
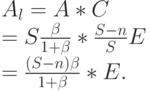 |
( 8.36) |
Продолжительность состояния i Оно является экспоненциально распределенным с интенсивностью:
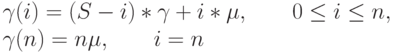 |
( 8.37) |
Функция увеличения:
 |
( 8.38) |
Выше мы определили вероятности состояния p(i), согласно предположению о статистическом равновесии, как часть времени, которое система находится в состоянии i, то есть как математическое ожидание времени. Мы можем также исследовать, как выглядит система, когда выполняется равновесие между поступлением и возвратом вызова отправляющим источником (пользователем) (математическое ожидание вызова). Если мы рассматриваем одну единицу времени то, в среднем, в системе будет 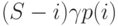 источников в состоянии [i] перед моментом поступления вызова, и если вызов принят, то он переведёт систему в состояние [i+1].
источников в состоянии [i] перед моментом поступления вызова, и если вызов принят, то он переведёт систему в состояние [i+1].
Источники, которые наблюдают систему в состоянии п, блокированы или остаются свободными. Поэтому источники, от которых поступает вызов прибытия, наблюдают систему в состоянии [i] с вероятностью:
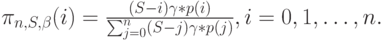 |
( 8.39) |
Используя метод аналогового дифференцирования выражения (8.27), мы можем показать, что в соответствии с теоремой поступления (Теорема 8.1) мы имеем:
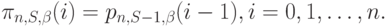 |
( 8.40) |
Когда источник оставляет систему, система находится в состоянии [i-1] с вероятностью:
 |
( 8.41) |
Применяя уравнения сечения, мы немедленно убеждаемся, что это соотношение идентично (8.39), если включить в рассмотрение блокированных абонентов. Таким образом, источники покидают систему в том же самом состоянии, в котором они в нее прибывают. Процесс будет, обратим и нечувствителен к распределению времени обслуживания. Если бы мы непрерывно наблюдали состояние системы, то не могли бы определить, выполняется ли время прямое действие (вызов) или обратный (выход из системы).
Отношения между Е, В и С
Из (8.34) мы получаем следующее отношение между 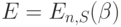 и
и 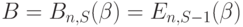
 |
( 8.42) |
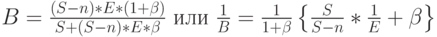 |
( 8.43) |
Выражения с правой стороны линейны по отношению к вероятностям блокировки. В (8.32) мы получили следующее простое отношение между С и Е:
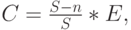 |
( 8.44) |
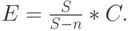 |
( 8.45) |
Если мы в (8.44) подставим Е, выраженное через (8.42), то мы получаем С, выраженное через В:
 |
( 8.46) |
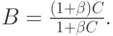 |
( 8.47) |
Это отношение между В и С является общим и может также быть получено следующим образом. Обслуженная нагрузка Y соответствует  принятых попыток вызова в единицу времени. Среднее число свободных источников - (S-Y), так что среднее число попыток вызова в единицу времени -
принятых попыток вызова в единицу времени. Среднее число свободных источников - (S-Y), так что среднее число попыток вызова в единицу времени -  (8.35).
(8.35).
Потери по вызовам тогда равны:
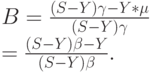
По определению Y= (1 - C), и из (8.20) имеем 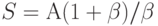 . Подставляя это выражение, мы имеем:
. Подставляя это выражение, мы имеем:
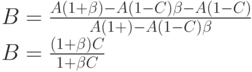
Из последнего уравнения видно, что для малых значений потерь по вызовам В потери по нагрузке Z в несколько раз больше, чем потери по вызовам:
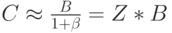 |
( 8.48) |
Расчеты по формуле Энгсета
Если мы пробуем вычислить числовые значения непосредственно по формуле Энгсета из (8.26) (потери по времени Е ), то возникают проблемы расчета для больших значений S и п. Ниже мы получим различные рекурсивные формулы для Е и для его обратной величины 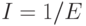 . Когда потери по времени Е известны, можно просто получить потери по вызовам В и потери по нагрузке С, используя формулы (8.43) и (8.44). В числовой форме также просто найти любой из этих четырех параметров
. Когда потери по времени Е известны, можно просто получить потери по вызовам В и потери по нагрузке С, используя формулы (8.43) и (8.44). В числовой форме также просто найти любой из этих четырех параметров 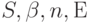 , когда мы знаем три из них. Математически мы можем предположить, что п и S не являются целыми числами.
, когда мы знаем три из них. Математически мы можем предположить, что п и S не являются целыми числами.
Рекурсивная формула для п
Из общей, рекурсивной формулы (7.27) для я, используя 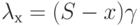 и
и  , мы получаем
, мы получаем
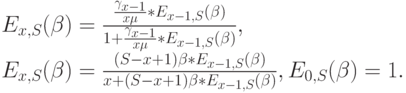 |
( 8.50) |
Используя обратную формулу потерь по времени 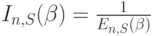 , мы находим рекурсивную формулу:
, мы находим рекурсивную формулу:
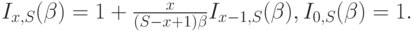 |
( 8.51) |
Число итераций равно п. Обе формулы (8.50) и (8.51) аналитически точны и представляют собой устойчивые при приближенных вычислениях и точные рекурсии для растущих значений х. Однако для уменьшающихся значений х числовые ошибки накапливаются и рекурсии недостоверны.
Рекурсивная формула по S
Обозначим нормализованные вероятности состояния системы с п каналами и S-1 источниками 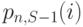 . Мы получаем вероятности состояния системы с S источниками и п каналами, сочетая эти вероятности состояния с вероятностями состояния одиночного источника, которые обозначаются
. Мы получаем вероятности состояния системы с S источниками и п каналами, сочетая эти вероятности состояния с вероятностями состояния одиночного источника, которые обозначаются 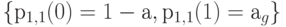 . Мы тогда получим состояние от нуля до п + 1, ограничиваем пространство состояний до n и нормализуем вероятности состояния (см. Пример 3.2.1) (принимая, что р(х) = 0, когда x < 0 ):
. Мы тогда получим состояние от нуля до п + 1, ограничиваем пространство состояний до n и нормализуем вероятности состояния (см. Пример 3.2.1) (принимая, что р(х) = 0, когда x < 0 ):
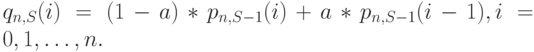 |
( 8.52) |
Полученные вероятности состояния 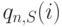 не нормализованы, потому что мы ограничиваем состояния числом [n] и исключаем последние элементы, начиная с состояния
не нормализованы, потому что мы ограничиваем состояния числом [n] и исключаем последние элементы, начиная с состояния ![[n+1], q_{n,S}(n+1)=a*р_{m,S-1}(n)](/sites/default/files/tex_cache/947f2ea271c93a32bd1bffd3b06a1b05.png) . Нормализованная вероятность состояния
. Нормализованная вероятность состояния 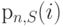 для системы с S источниками и п каналами, таким образом, получается из нормализованной вероятности состояния
для системы с S источниками и п каналами, таким образом, получается из нормализованной вероятности состояния 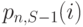 для системы с
для системы с 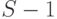 источником:
источником:
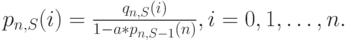 |
( 8.53) |
Потери по времени 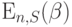 для системы с S источниками могут быть выражены потерями по времени
для системы с S источниками могут быть выражены потерями по времени 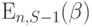 для системы с S-1 источниками. Подставляя (8.52) в (8.53), получаем:
для системы с S-1 источниками. Подставляя (8.52) в (8.53), получаем:
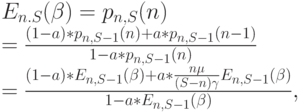
где мы использовали уравнение равновесия между состоянием [n-1, S - 1] и состоянием [n, S-1]. Заменяя а на(8.8), мы получаем:
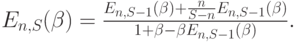
Таким образом, получаем следующую рекурсивную формулу:
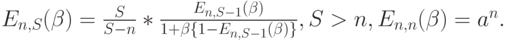 |
( 8.55) |
Начальное значение получено от (8.12). Находим обратное значение вероятности блокировки I= 1/E:
 |
( 8.56) |
Для того чтобы увеличить S, нужно, чтобы число итераций было S-n. Однако числовые ошибки накапливаются из-за умножения с (S/(S-n)) таких умножений больше чем одно, и применимость этой формулы ограничена. Поэтому рекомендуют использовать рекурсию (8.58), приведенную в следующей секции для того, чтобы увеличить S. Чтобы уменьшить S, вышеупомянутая формула аналитически точна и в числовой форме устойчива. Однако начальное значение должно быть известно заранее.
Рекурсивная формула и по n и по S
Если подставить (8.50) в (8.55), соответственно (8.51) в (8.56), мы находим:
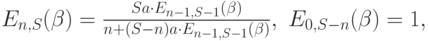 |
( 8.57) |
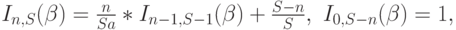 |
( 8.58) |
которые являются рекурсивными и относительно числа обслуживающих приборов, и относительно числа источников. Обе из этих рекурсий в числовой форме точны при процессе увеличения показателей и числа итераций n (Joys, 1967 [54]).
Из материалов, рассмотренных выше, мы можем сделать следующие заключения для рекурсивной формулы Энегсета. При вычислении с увеличением значения параметра рекурсивные формулы (8.50) и (8.51) очень точны, и формулы (8.57), и (8.58) почти хороши. Рекурсивные формулы (8.55) и (8.56) неточны при увеличении значения параметра, но в отличие от других, устойчивы при уменьшении значения. Вообще, можно заметить, что рекурсия, которая является точной в одном направлении, будет неточна в противоположном направлении.
Пример 8.5.1: система с потерями Энгсета
Мы рассматриваем систему с потерями Энгсета, имеющую n=3 канала и S= 4 источника. Скорость поступления вызовов от свободного источника - 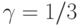 вызовов в единицу времени, и среднее время обслуживания (
вызовов в единицу времени, и среднее время обслуживания ( 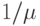 ) равно 1 в единицу времени. Мы находим следующие параметры:
) равно 1 в единицу времени. Мы находим следующие параметры:
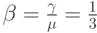 |
Эрл. ( предложенная нагрузка на один свободный источник); |
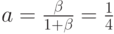 |
Эрл. ( предложенная нагрузка на один свободный источник); |
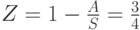 |
(пиковость). |
Из диаграммы переходов состояний мы получаем следующую таблицу:
 |
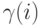 |
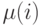 |
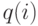 |
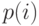 |
 |
 |
|---|---|---|---|---|---|---|
| 0 | 4/3 | 0 | 1.0000 | 0.3176 | 0.0000 | 0.4235 |
| 1 | 3/3 | 1 | 1.3333 | 0.4235 | 0.4235 | 0.4235 |
| 2 | 2/3 | 2 | 0.6667 | 0.2118 | 0.4235 | 0.1412 |
| 3 | 1/3 | 3 | 0.1481 | 0.0471 | 0.1412 | 0.0157 |
| Total | 3.1481 | 1.0000 | 0.9882 | 1.0039 |
Мы находим следующие вероятности блокировки.
Потери по времени:
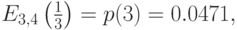
Потери по нагрузке:
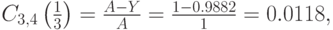
Потери по вызовам:

Заметим, что Е>В>С, и это является общим результатом для модели Энгсета (8.49) и (рис.8.6).
Применяя рекурсивную формулу (8.51) мы, конечно, получаем те же самые результаты: