|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Система с потерями и В-формула Эрланга
Характеристики нагрузки Пуассоновского распределения
С точки зрения измерения нагрузки, система с бесконечным числом линий не очень интересна. Просмотрим важные характеристики нагрузки системы с потерями.
Потери по времени 
Потери по вызовам 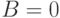
Обслуженная нагрузка 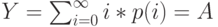 ,
,
Потерянная нагрузка  ,
,
Потери по нагрузке 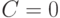
Нагрузка, которая обслужена  -той линией, принимающей последовательную нагрузку, дается позже в (7.14).
-той линией, принимающей последовательную нагрузку, дается позже в (7.14).
Пиковость Z определяется как отношение между дисперсией и средней величиной распределения вероятностей состояния.
Для Пуассоновского распределения мы находим (6.17) и (6.18):
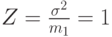 |
( 7.7) |
Пиковость имеет размерность [число каналов] и отличается от коэффициента вариации, который не имеет никакого измерения (3.9).
Продолжительность состояния [i]
В состоянии ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) процесс имеет полную интенсивность
процесс имеет полную интенсивность 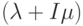 . Поэтому время до первого перехода (переход из состояния
. Поэтому время до первого перехода (переход из состояния  либо к
либо к  , либо к
, либо к 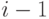 ) - распределено по экспоненте (секция 4.1.1):
) - распределено по экспоненте (секция 4.1.1):

Пример 7.2.1: Протокол простая АЛОХАа
В примере 6.2.2 мы рассматривали протокол синхронная (сегментированная) АЛОХАа, где оси времени были разделены на слоты времени. Мы теперь рассматриваем тот же самый протокол в непрерывное время. Предположим, что пакеты прибывают согласно Пуассоновскому процессу и что они имеют постоянную длину  . Система соответствует случаю нагрузки, заканчивающемуся Пуассоновским распределением, которое также является справедливым для постоянных времен занятия (секция 7.2). Вероятности состояния отображаются Пуассоновским распределением (7.6), где
. Система соответствует случаю нагрузки, заканчивающемуся Пуассоновским распределением, которое также является справедливым для постоянных времен занятия (секция 7.2). Вероятности состояния отображаются Пуассоновским распределением (7.6), где 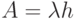 . Пакет передается правильно, если: (а) система находится в состоянии [0] во время прибытия и (б) никакие другие пакеты не поступают в течение времени обслуживания
. Пакет передается правильно, если: (а) система находится в состоянии [0] во время прибытия и (б) никакие другие пакеты не поступают в течение времени обслуживания  . Мы находим:
. Мы находим:
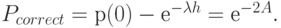
Переданная правильно нагрузка, таким образом, получается:

Это - соотношение оси времени, при эффективном использовании оно имеет оптимум для 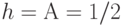 , где производная относительно
, где производная относительно  равняется нулю:
равняется нулю:
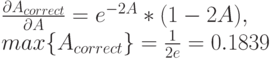 |
( 7.8) |
Мы, таким образом, получаем, что максимальное использование равно 0.1839, когда предложение равно 0.5 Эрл. Это - половина значения, которое мы получили для системы, использующей слоты в синхронных спутниковых передатчиках. Сравнение различных моделей АЛОХА уже было сделано на рис.6.4.
Усеченное Пуассоновское распределение
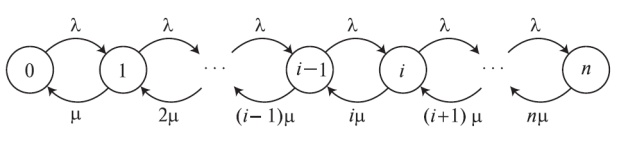
Мы рассматриваем вариант, когда Чистая Случайная Нагрузка I (PCT-I) такая же, как в секции 7.2. Число каналов теперь ограничено и я конечно. Число состояния становится  , диаграмма Чистая Случайная Нагрузка I при переходе состояний показана на рис.7.2.
, диаграмма Чистая Случайная Нагрузка I при переходе состояний показана на рис.7.2.
Диаграмма переходов состояний схематически изображает систему с ограниченным числом каналов  , Пуассоновский поток вызовов
, Пуассоновский поток вызовов  и экспоненциальное время обслуживания
и экспоненциальное время обслуживания  )
)
Вероятности состояния
Мы получаем уравнения сечения, как и в случае Пуассоновского процесса, но пространство состояний ограничено  и условие нормализации (7.5) теперь равно:
и условие нормализации (7.5) теперь равно:

Мы получаем так называемое усеченное Пуассоновское распределение (первая формула Эрланга):
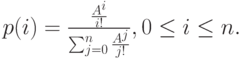 |
( 7.9) |
Название усеченное означает "укороченное" вследствие того, что решение может интерпретироваться как усеченное Пуассоновское распределение 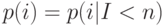 . Это легко увидеть, умножая числитель и знаменатель на
. Это легко увидеть, умножая числитель и знаменатель на 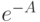 .
.
Характеристики нагрузки В-формулы Эрланга
Зная вероятности состояния, мы можем найти критерии качества работы, определяемые этими вероятностями состояния.
Потери по времени
Вероятность, что все  каналов заняты в случайный момент времени, равна отношению всего времени работы ко времени занятости всех каналов (математическое ожидание времени). Это видно из (7.9) для
каналов заняты в случайный момент времени, равна отношению всего времени работы ко времени занятости всех каналов (математическое ожидание времени). Это видно из (7.9) для 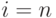 :
:
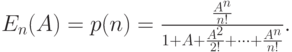 |
( 7.10) |
Это - известная В-формула Эрланга (1917, [11]). Она обозначается  , где указатель "1" рассматривается как указатель названия первая формула Эрланга.
, где указатель "1" рассматривается как указатель названия первая формула Эрланга.
Потери по вызовам
Вероятность, что случайный вызов будет потерян, равна отношению всех попыток вызовов к числу блокированных попыток вызова. Если мы рассматриваем единицу времени, то находим 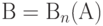 :
:
 |
( 7.11) |
Обслуженная нагрузка
Если мы используем усеченное уравнение между состоянием ![[i-1]](/sites/default/files/tex_cache/7382a273ce9521676070f42215bf6956.png) , и
, и ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) , то получим:
, то получим:
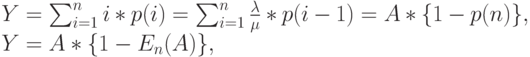 |
( 7.12) |
где А - предложенная нагрузка. Обслуженная нагрузка будет меньше и чем А, и чем п.
Потери по нагрузке
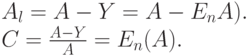
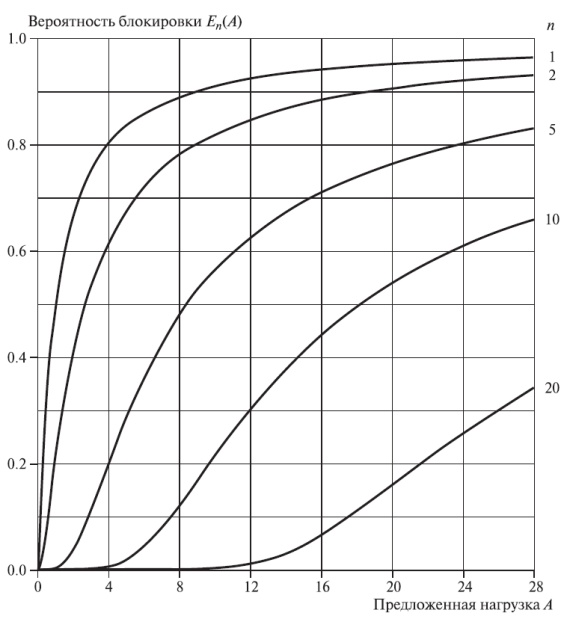
Мы, таким образом, имеем Е=В=С, потому что интенсивность вызова не зависит от состояния. Это свойство - PASTA (Poisson Arrivals See Time Averages - Пуассоновское поступление вызовов, наблюдаемое за среднее время) - справедливо для всех систем с Пуассоновскими потоками вызовов. Во всех других вариантах, по крайней мере, два из трех случаев потерь различны. В-формула Эрланга показана графически на рис. 7.3 для некоторых выбранных значений параметров.
Нагрузка, которую обслуживает i -ый канал (использование 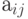 )
)
-
Случайный поиск. В этом случае все каналы в среднем обслуживают одну и ту же нагрузку. Полная обслуженная нагрузка не зависит от стратегии поиска, и мы можем найти использование:
Вероятность блокировки
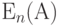 как функция предложенной нагрузки для различных значений числа каналов -
как функция предложенной нагрузки для различных значений числа каналов -  (7.9)
(7.9)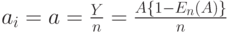
( 7.13) Эта функция показана на рис. 7.4, и мы наблюдаем, что в данном случае при потерях Е получается самое высокое использование для больших групп канала (экономия из-за масштаба).
-
Обусловленный поиск - последовательный поиск: нагрузка, которую обслуживает канал, есть разность между нагрузкой, потерянной i-1 каналами, и нагрузкой, потерянной i каналами:
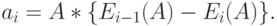
( 7.14) Отметим, что нагрузка, которую обслуживает канал i, не зависит от общего числа каналов. Таким образом, каналы после i -того канала не влияют на нагрузку, обслуживаемую каналом i, т.е. между каналами нет никакой обратной связи.
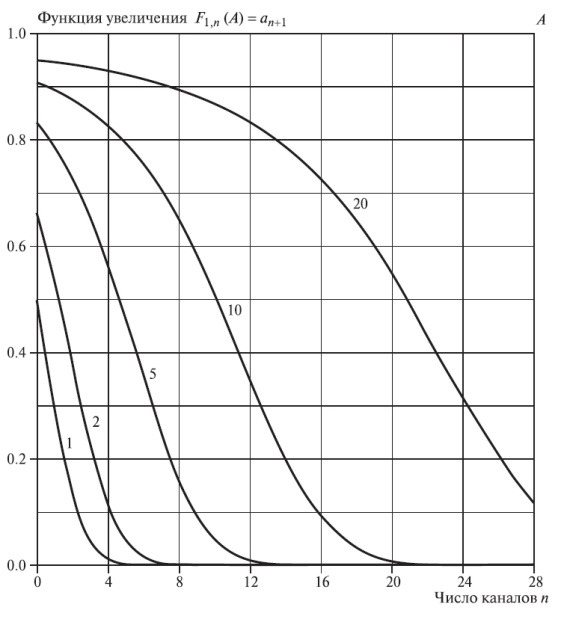
Функция увеличения
Она обозначает увеличение обслуженной нагрузки, когда число каналов увеличено на один от n до n + 1:
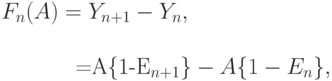 |
( 7.15) |
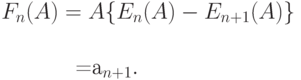 |
( 7.16) |
Мы имеем 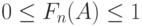 ..
..
Функция увеличения Fn (А) сведена в таблицу (Арн Дженсен, 1950 [50]) и показана на рис.7.5. В секции 7.6.2 мы рассматриваем приложение этого принципа для оптимального экономичного измерения нагрузки.
Пиковость
Она определяется как отношение между дисперсией и средней величиной распределения числа занятых каналов, сравните с IDC (Индексрассеяния для расчетов - Index of Dispersion for Counts) (5.11). Для усеченного Пуассоновского распределения, используя (7.14), можно показать
 |
( 7.17) |
Размерность - [число каналов]. В группе с обусловленным поиском мы можем таким образом оценить пиковость нагрузки, которую обслуживает последний канал.
Функция увеличения 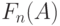 (7.16) по В формуле Эрланга.
(7.16) по В формуле Эрланга. 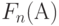 при последовательном поиске равна нагрузке
при последовательном поиске равна нагрузке 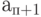 , при увеличении числа канала
, при увеличении числа канала 
Продолжительность состояния [i]
Полная интенсивность для перехода из состояния ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) постоянна и равна
постоянна и равна 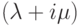 , и поэтому продолжительность времени в состоянии
, и поэтому продолжительность времени в состоянии ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) (время пребывания) экспоненциально распределена с функцией плотности:
(время пребывания) экспоненциально распределена с функцией плотности:
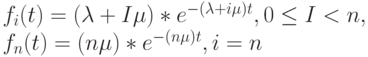 |
( 7.18) |