|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Пуассоновский процесс
Пример 6.2.2: Спутниковая система синхронного (сегментированная) АЛОХА
ALOHA - метод случайного доступа, принцип которого состоит в том, что все станции работают в одном канале связи, контролируя его работу, а передача осуществляется в случайные моменты времени. Когда две или более станций передают пакет в один и тот же момент времени (или перекрывавшиеся интервалы), приемник оказывается не способен правильно его принять. Поэтому при возникновении подобных ситуаций осуществляется повторная передача пакетов через случайный интервал времени. Различают два метода доступа: "чистая" (несегментированная) АЛОХА и сегментированная синхронная АЛОХА. В первом случае повторение передачи осуществляется в случайное время, во втором - в синхронные промежутки времени.
Рассмотрим цифровую спутниковую систему связи с постоянной длиной пакета  :
:
Спутник находится на геостационарной позиции приблизительно в 36.000 км выше уровня экватора, так что задержка распространения туда и обратно - приблизительно 280 мсек., а ось времени разделена на слоты фиксированной продолжительности, соответствующей длине пакета  .
.
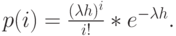 |
( 6.19) |
Это соответствует соотношению осей времени, которое используется эффективно. Эта функция, как показывает рис.6.4, имеет оптимум для 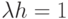 , так как производная по
, так как производная по 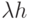 равна нулю.
равна нулю.
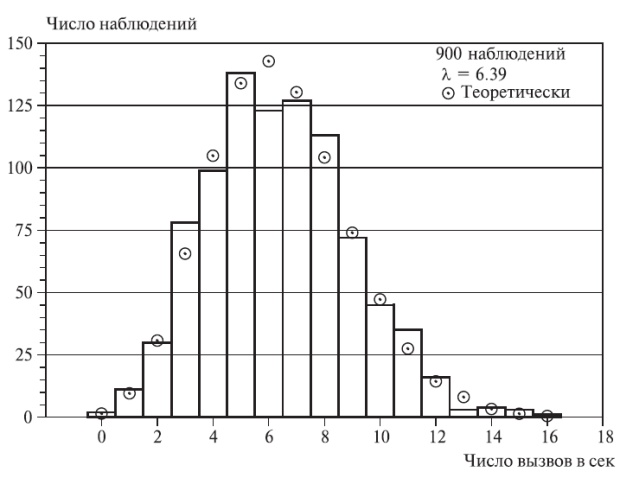
Рис. 6.3. Число вызовов в секунду для автоматического соединения с набором номера. Теоретические значения получены при условии Пуассоновского распределения. При статистических испытаниях принята гипотеза Пуассоновского распределения.
Для этих условий:
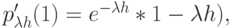 |
( 6.21) |
 |
( 6.22) |
Таким образом, имеем максимальное использование канала, равное 0.3679, когда в среднем мы передаем один временной слот на пакет. Подобный результат сохраняется, когда число терминалов ограничено, и число временных слотов на пакет распределено биноминально.
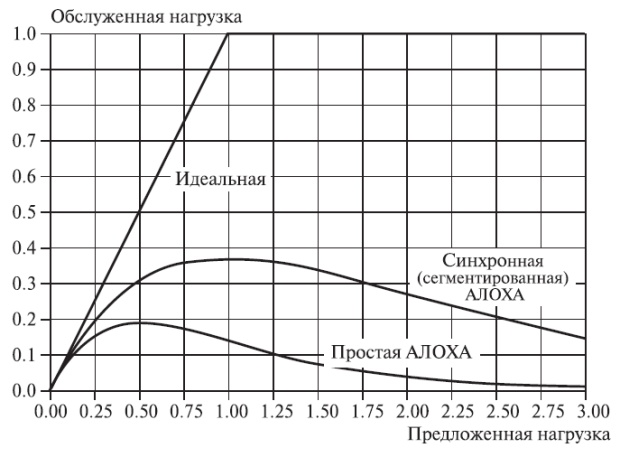
Рис. 6.4. Обслуженная нагрузка в системе синхронной (сегментированной) АЛОХА имеет максимум (пример 6.2.2). С простым протоколом АЛОХА мы будем иметь дело в примере 7.2.1.
Статическое получение распределения Пуассоновского процесса
Как известно из статистики, Пуассоновские распределения могут также быть получены из биноминального процесса, если число испытаний  (например, число бросков игральной кости), увеличивается до бесконечности. В то же самое время вероятность успеха в единственном испытании
(например, число бросков игральной кости), увеличивается до бесконечности. В то же самое время вероятность успеха в единственном испытании 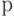 стремится к нулю, таким образом, чтобы среднее число успехов
стремится к нулю, таким образом, чтобы среднее число успехов  было постоянным.
было постоянным.
Этот подход является статическим и не подчеркивает фундаментальные свойства Пуассоновского процесса, который основан на динамических свойствах. Однако такой подход определяется отношениями между двумя процессами, как это проиллюстрировано в Таблице 6.1.
|
БИНОМИНАЛЬНЫЙ ПРОЦЕСС Дискретное время Вероятность успеха: 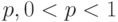
|
ПУАССОНОВСКИЙ ПРОЦЕСС Непрерывное время Интенсивность успеха: |
| Число попыток начиная с предыдущего успеха или начиная со случайной попытки получить успех | Интервал между двумя успехами или от случайной точки до следующего успеха |
|
ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ 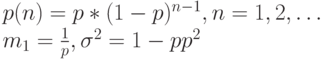
|
ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 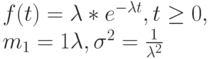
|
Число попыток получить  успехов успехов |
Временной интервал до  ' того успеха ' того успеха |
|
ПАСКАЛЬ - ОТРИЦАТЕЛЬНОЕ БИНОМИНАЛЬНОЕ РАСПРЕДЕЛНИЕ 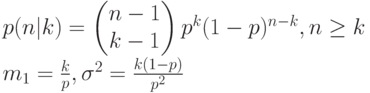
|
РАСПРЕДЕЛЕНИЕ ЭЛАНГА К-ПОРЯДКА 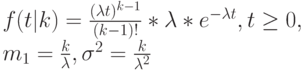
|
Число успехов в 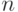 попытках попытках |
Число успехов во временном интервале 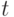
|
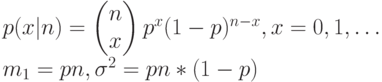
|
ПУАССОНОВСКОЕ РАСПРЕДЕДЕНИЕ 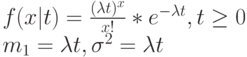
|
Экспоненциальное распределение - единственное непрерывное распределение с отсутствием памяти, и геометрическое распределение - единственное дискретное распределение с отсутствием памяти. Например, следующий результат броска игральной кости не зависит от предыдущего результата. Распределения этих двух процессов показано в Таблице 6.1.
Свойства Пуассоновского процесса
В этой секции мы покажем некоторые фундаментальные свойства Пуассоновского процесса. При рассмотрении физической модели в секции 6.2 мы видели, что Пуассоновский процесс - самый случайный точечный процесс, который может быть найден ( процесс с максимальным беспорядком ). Это дает возможности хорошо описать физические процессы и много различных факторов всего процесса.
Теорема Пальма (теорема Суперпозиции)
Фундаментальные свойства Пуассоновского процесса среди всех других точечных процессов были сначала рассмотрены шведом К. Пальмом. Он показал, что экспоненциальные распределения играют для стохастических точечных процессов ту же самую роль (например, распределение времени интервала), где точечные процессы представлены суперпозицией, как это делается при нормальном распределении, когда стохастические переменные складываются (центральная предельная теорема).
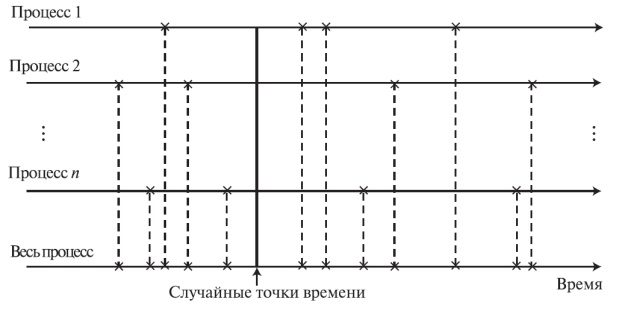
Рис. 6.5. В результате суперпозиции п точечных процессов получается процесс, который при некоторых предположениях является локальным Пуассоновским.
Теорема 6.1. Пальм: суперпозиция многих независимых точечных процессов дает в результате полный локальный Пуассоновский процесс.
Термин "локальный" означает, что мы рассматриваем временные интервалы, которые настолько малы, что каждый процесс в течение этого интервала вносит вклад не более чем в одно событие. Это - естественное требование, так как ни один процесс не может доминировать над полным процессом (подобные условия приняты для центральной предельной теоремы). Теорема справедлива только для простых точечных процессов. Если мы рассматриваем случайный момент времени в некотором процессе, то время до следующего прибытия можно определить с помощью (3.23).
Мы собираем  процессов в один полный процесс. Выбирая соответствующий шаг времени между поступлением заявок, можно получить из
процессов в один полный процесс. Выбирая соответствующий шаг времени между поступлением заявок, можно получить из  независимых процессов полный процесс. Время от случайной точки времени до следующего события в полном процессе тогда определяется (3.23).
независимых процессов полный процесс. Время от случайной точки времени до следующего события в полном процессе тогда определяется (3.23).
Если все подпроцессы идентичны, мы получаем:
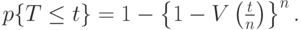 |
( 6.24) |
Из (3.23) и (5.18) мы находим (разрешение 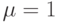 ):
):

И, таким образом:
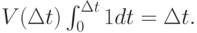 |
( 6.25) |
Увеличивая число подпроцессов до бесконечности, мы получаем из (6.24),
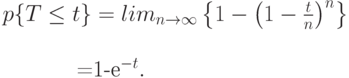 |
( 6.26) |
что является экспоненциальным распределением. Мы, таким образом, показали, что суперпозицией идентичных процессов получаем локальный Пуассоновский процесс. Подобным способом мы можем сложить неидентичные процессы и получить локальный Пуассоновский процесс.
Пример 6.3.1: Время "жизни" маршрута в сети
Маршрут в сети состоит из множества линий связи, соединяющих конечные точки маршрута (Лекция 11). Для данного случая соединения в сети существуют на ограниченный период времени. Время "жизни" маршрута - это время, пока не будет разъединена одна из линий. Из теоремы Пальма мы видим, что время "жизни" маршрута имеет тенденцию быть экспоненциально распределенным.
Теорема Райкова (теорема Разложения)
Эта теорема - теорема разложения, она относится к случаю, когда мы случайным образом разбиваем точечный процесс на подпроцессы. Если число интеравлов времени  меньше числа событий в подпроцессе то, естественно, уменьшить оси времени с коэффициентом
меньше числа событий в подпроцессе то, естественно, уменьшить оси времени с коэффициентом  .
.
Теорема 6.2. Теорема Райкова: При случайном разложении точечного процесса на подпроцессы, каждый отдельный подпроцесс сходится к Пуассоновскому процессу, если вероятность, что событие принадлежит подпроцессу, стремится к нулю.
Также отмечается следующий общий результат. Если мы генерируем подпроцесс случайным разбиением точечного процесса, выбирая событие с вероятностью 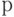 , то подпроцесс имеет коэффициент формы
, то подпроцесс имеет коэффициент формы
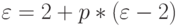
где е является коэффициентом формы первоначального процесса.
В дополнении к объединению или разъединению, мы можем с точечным процессом сделать другие операции, а именно перенос (смещение) отдельных событий. Если этот перенос для каждого события - случайная переменная, независимая от всех других событий, произвольный точечный процесс будет сходиться к Пуассоновскому процессу.
Что касается появления точечных процессов в реальной жизни, мы согласно перечисленному выше можем ожидать что, когда события подчиняются достаточно большому числу независимых условий, они - Пуассоновские процессы. Вот почему Пуассоновский процесс - это, например, хорошее описание процессов поступления вызовов к местной станции от всех местных абонентов.
Как пример ограничений в теореме Пальма (Теорема 6.1) можно показать , что суперпозиция двух независимых процессов является Пуассоновским процессом, только когда оба подпроцесса - Пуассоновские процессы.
Однородное распределение -условное свойство
В секции 6.2 мы видели, что однородное распределение в очень большом интервале соответствует Пуассоновскому процессу. Обратное свойство также правильно.
Теорема 6.3. Если для Пуассоновского процесса мы имеем п поступлений заявок в пределах интервала продолжительностью 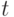 , тогда эти поступления, однородно распределены в пределах этого интервала.
, тогда эти поступления, однородно распределены в пределах этого интервала.
Длина этого интервала может быть самостоятельной случайной переменной, если она подчиняется независимому Пуассоновскому процессу. Это, например, имеет место при измерении трафика с переменным интервалом измерения (Лекция 15). Можно показать верность утверждения и для Пуассоновского распределения (числовое представление), и для экспоненциального распределения (представление интервала).
Обобщение стационарного Пуассоновского процесса
Пуассоновский процесс был обобщен многими способами. В этой секции мы рассматриваем только прерывистый Пуассоновский процесс и дальнейшие обобщения: MMPP (Markov Modulated Poisson Processes - марковские процессы, модулируемые Пуассоновскими процессами) и MAP (Markov Arrival Processes - марковские Процессы поступления вызовов).
Прерывистый Пуассоновский процесс (IPP - Interrupted Poisson process)
Из-за отсутствия памяти Пуассоновский процесс очень прост в применении. В некоторых случаях, однако, Пуассоновский процесс не достаточен, чтобы описать реальный процесс поступления вызовов, так как имеется только один параметр. Качура (Kuczura 1973 [70]) предложил обобщение, которое широко использовалось в дальнейшем.
Идея обобщения вытекает из проблемы перегрузки (рис.6.6 и секция 9.2). Вызовы от клиентов, работающих с системой, будут сначала поступать на обслуживание первичной системой с ограниченной емкостью (только  серверов). Если первичная система занята, то поступления вызовов будут обслуживаться системой перегрузки. Поступления вызовов направляют к системе перегрузки только тогда, когда первичная система занята.
серверов). Если первичная система занята, то поступления вызовов будут обслуживаться системой перегрузки. Поступления вызовов направляют к системе перегрузки только тогда, когда первичная система занята.
В течение периодов занятости клиенты поступают в систему перегрузки согласно Пуассоновскому процессу с интенсивностью  .
.
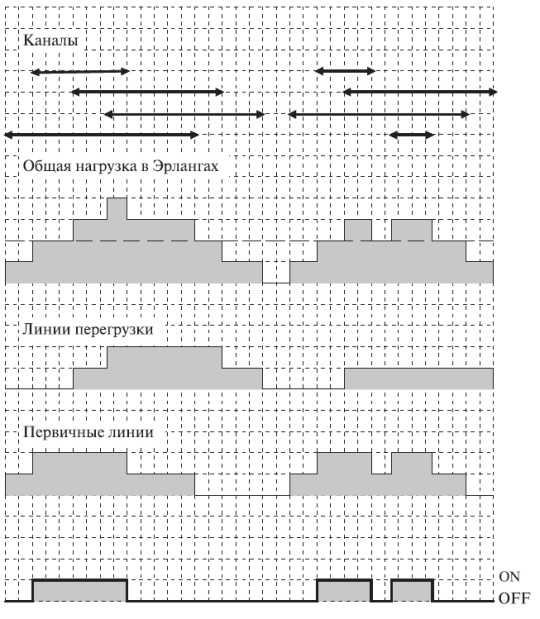
Рис. 6.6. Перегруженная система с Пуассоновским потоком вызовов. Обычно вызовы прибывают в первичную группу линий. В течение периодов, когда все n магистралей в первичной группе линий заняты, все вызовы предлагаются группе линий перегрузки.
В течение периодов свободности ни один вызов не прибывает в систему перегрузки, то есть интенсивность прибытия является нулевой. Таким образом, мы можем рассматривать процесс поступления вызовов в систему перегрузки как Пуассоновский процесс, который либо Включен ( ОN ), либо Выключен ( 0FF ) (рис. 6.7). Как упрощенную модель, чтобы описать эти интервалы ON (OFF), Качура использовал экспоненциально распределенные временные интервалы с интенсивностью 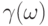 . Он показал, что межинтервальные времена прибытия к линии связи перегрузки соответствуют гиперэкспоненте.
. Он показал, что межинтервальные времена прибытия к линии связи перегрузки соответствуют гиперэкспоненте.
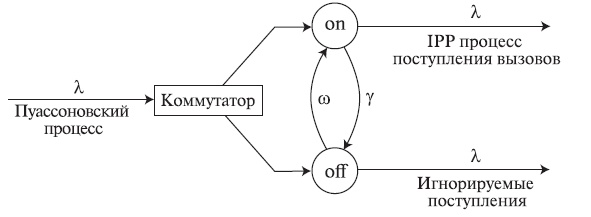
Рис. 6.7. Иллюстрация прерывистого Пуассоновского процесса (IPP) (сравните Рис. 6.6). Позиция коммутатора управляется марковским процессом с двумя состояниями.
Они могут быть проиллюстрированы фазовой диаграммой (рис. 6.8). Можно показать, что параметры связаны следующим образом:
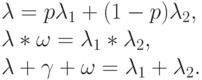 |
( 6.28) |
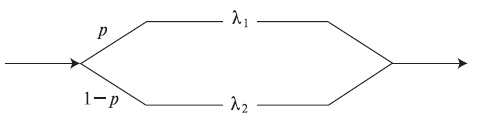
Рис. 6.8. Прерывистый Пуассоновский процесс эквивалентен гиперэкспоненциальному процессу поступления вызовов (6.28)
Поскольку гиперэкспоненциальное распределение с двумя фазами может быть преобразовано в распределения Кокса 2 (секция. 4.4.2), IРР -процесс поступления вызовов есть процесс поступления вызовов Кокса 2, как показано на рис.4.10. Мы имеем три параметра, тогда как Пуассоновский процесс имеет только один параметр. Это делает его более гибким для моделирования различных эмпирических данных.
Краткие итоги
- Пуассоновский процесс - самый важный точечный процесс. Позже мы поймем, что его роль среди точечных процессов столь же фундаментальная, как роль Нормального распределения среди статистических распределений.
- Фундаментальные свойства Пуассоновского процесса: стационарность, независимость (отсутствие последействия) и простота (ординарность). Пуассоновский процесс, обладающий всеми тремя свойствами, называется простейшим.
- Числовое представление Пуассоновского процесса: число событий в пределах временного интервала фиксированной длины имеет Пуассоновское распределение.
- Представление с помощью интервала Пуассоновского процесса: интервал времени
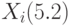 между последовательными событиями является экспоненциально распределенным.
между последовательными событиями является экспоненциально распределенным. - Существенный шаг в развитии Пуассоновского распределения - получение вероятности
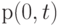 , которая является вероятностью непоступления заявки в пределах временного интервала длины
, которая является вероятностью непоступления заявки в пределах временного интервала длины 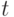 , то есть вероятности, что первое поступление заявки произойдет позже, чем
, то есть вероятности, что первое поступление заявки произойдет позже, чем 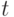 .
. - Время поступления точно
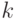 событий определяется суммой
событий определяется суммой 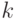 независимо экспоненциально распределенных случайных переменных. Распределение этой суммы - это
независимо экспоненциально распределенных случайных переменных. Распределение этой суммы - это 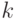 - распределение Эрланга.
- распределение Эрланга. -
Вероятность
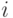 -ого поступления заявки в пределах временного интервала
-ого поступления заявки в пределах временного интервала 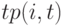
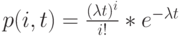
-
Пуассоновское распределение может быть получено из биноминального процесса, если число испытаний
 стремится к бесконечности.
стремится к бесконечности. - Суперпозиция многих независимых точечных процессов дает в результате полный локальный Пуассоновский процесс.
- Прерываемый Пуассоновский процесс можно рассматривать как процесс поступления вызовов в систему с переключателем на систему перегрузки.

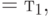 дисперсия
дисперсия 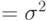 . Для геометрического распределения мы можем начинать с числа попыток, равного 0. Математическое ожидание тогда уменьшается, а дисперсия остается той же самой.
. Для геометрического распределения мы можем начинать с числа попыток, равного 0. Математическое ожидание тогда уменьшается, а дисперсия остается той же самой.